Прямолинейно-параллельный фильтрационный поток

Фильтрационный поток называется прямолинейно- параллельным, когда траекториями частиц жидкости являются прямые линии, параллельные между собой, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения равны друг другу.

Наглядным примером такого фильтрационного потока является приток жидкости от прямолинейного контура питания к параллельной к нему прямолинейной батарее скважин, вскрывающих горизонтальный пласт постоянной ширины В на всю его толщину h =const. (рис. 6);

здесь: Р_к - давление на контуре питания; L_к – расстояние от контура питания до батареи скважин (галереи).

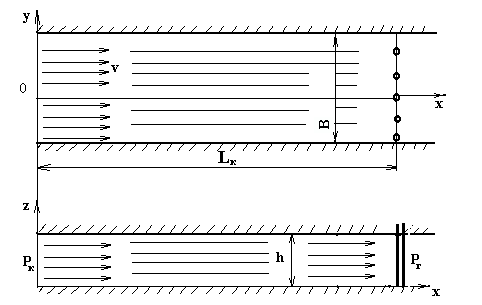
Рис.6

Законы движения частиц жидкости вдоль всех траекторий такого потока совершенно одинаковы, а поэтому для исследования принимаем одну из траекторий, по которой направляем координатную ось ОX, а ось ОY - вдоль контура питания.

Дифференциальное уравнение Лапласса (3.3) в данном случае принимает вид

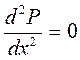. (3.7)

Для определения давления в любой точке потока дважды интегрируем уравнение (3.7) при следующих граничных условиях:

при X = 0 P = P_k = const;

при X = L_k P = P_г = const. (3.8)

В результате двухкратного последовательного интегрирования (3.7) находим

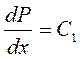или ,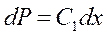

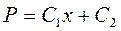, (3.9)

где С₁ и С₂ - произвольные постоянные. Подставляя в (3.9) граничные условия (3.8), получаем

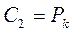;. (3.10)

Закон распределения давления находим, подставив значения С₁ и С₂ из (3.10) в выражение общего решения (3.9)

. (3.11)

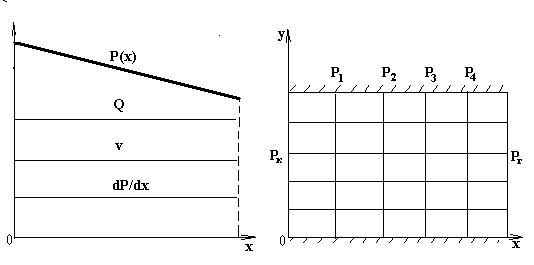Как следует из решения (3.11) пластовое давление Р(x) распределяется вдоль линии тока по линейному закону (рис. 7). В любой плоскости YOZ давление одинаково во всех точках, для которых X = const, т.е. это есть уравнение семейства изобар, перпендикулярных к линии тока OX; изобары и линии тока образуют два семейства взаимно перпендикулярных прямых линий (рис. 8).

Рис.7 Рис.8

Из (3.11) получаем выражение для градиента давления

. (3.12)

Уравнение движения для рассматриваемого случая, как это следует из (3.2), имеет вид:

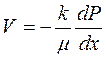. (3.13)

Подставив (3.12) в уравнение (3.13), находим выражение скорости фильтрации

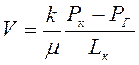. (3.14)

Объемный расход жидкости в потоке определяется произведением скорости фильтрации V на площадь поперечного сечения потока w = В*h, т.е

. (3.15)

Как видно из решений (3.12), (3.14) и (3.15) градиент давления dP/dx, скорость фильтрации V и расход (дебит) жидкости Q постоянны вдоль потока, т.е. не зависят от координаты X (рис. 7).

Закон движения частиц жидкости Х=Х(t) найдем, используя соотношение между скоростью фильтрации V и средней скоростью движения частиц жидкости V_Д

или ;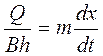

откуда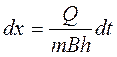

Интегрируя в пределах от 0 до t и от 0 до Х, получаем закон движения частиц жидкости

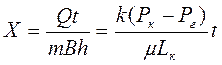, (3.16)

т.е. зависимость х =х(t) линейная, как и следовало ожидать, поскольку в рассматриваемых условиях фильтрационный поток движется с постоянной скоростью V (3.14).

Дата добавления: 2014-01-07