ЛЕКЦИЯ №3. Промежность (perineum)

Молочные железы

Промежность (perineum).

Образует дно таза. Ограничена:

· спереди – нижним краем лобкового симфиза,

· сзади – верхушкой копчика,

· по бокам – нижние ветви лобковых и седалищных костей и седалищные бугры.

Области:

· передняя мочеполовая область – расположены наружные половые органы, мочеиспускательный канал, влагалище, мышцы мочеполовой диафрагмы;

· заднепроходная область – промежностный отдел прямой кишки, задний проход, наружный заднепроходной сфинктер, мышцы тазовой диафрагмы.

Диафрагмы – это мышечно-фасщиальные пластинки, образованные двумя слоями мышц (поверхностными и глубокими) и фасциями.

Обе диафрагмы прилежат друг к другу своими основаниями, а вершинами направлены к лобковому симфизу и копчику.

Промежность покрыта тонкой пигментированной кожей, содержит потовые, сальные железы и редкие волосы.

Значение промежности:

1. выдерживает тяжесть внутренних органов;

2. выдерживает внутрибрюшное давление;

3. препятствует выпадению внутренних органов;

4. формирует произвольные сфинктеры мочеиспускательного канала и прямой кишки.

Молочные железы представляют собой видоизменённые потовые железы кожи. В каждой железе содержится 15-20 отдельных желёзок, или долек, которые разделены прослойками жировой и соединительной ткани. Именно благодаря жировой ткани, молочные железы приобретают полушаровидную форму.

Каждая железистая долька имеет выводной млечный проток. На своём значительном протяжении эти протоки расширены, образуя млечные синусы, в которых перед кормлением скапливается молоко.

Концевые части протоков сужены и открываются в соске железы млечными отверстиями. Число отверстий (8-15) немного меньше числа долек, т.к. некоторые протоки сливаются друг с другом.

Молочные железы относятся к сложным железам, так как протоки молочной железы ветвятся.

Лактирующая способность приобретается к концу беременности. Большую роль в преобразовании железы играет прогестерон, на фоне продукции которого протекает беременность. Прогестерон стимулирует в молочной железе разрастание млечных альвеолярных ходов и формирование на их концах альвеол, или ацинусов.

Осевое (центральное) растяжение (сжатие)

Трос подъемника, колонна, болт – подвергаются такому виду деформации.

Центральным растяжением (сжатием) называется такой вид деформации, при котором в поперечном сечении бруса (детали) возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние усилия равны нулю.

Рассмотрим простейший случай. Стержень сжат силой Р. Определим продольную силу в сечении I – I. Рассечем стержень по сечению. Возникают три силовых фактора N, Q, M, из которых Q, M тождественно равны нулю.

Рассмотрим равновесие левой отсеченной части.

Составляя уравнение ΣX=0, получим P-N=0; N=P. (сжатие)

Правило знаков для продольной силы N:

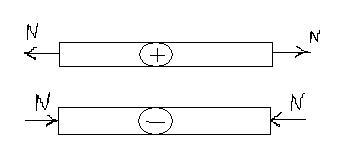Если N направлена от сечения, то растяжение знак +;

N направлена к сечению, то сжатие знак –.

Рассмотрим более сложный случай:

Действуют две силы. Также рассматриваем равновесие левой отсеченной части.

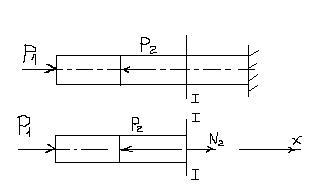ΣX=0 P₁ – P₂ + N₂=0

N₂=P₂ – P₁

N₂ - проекция всех сил по одну сторону сечения.

Продольная сила, действующая в поперечном сечении стержня, численно равна алгебраической сумме проекций всех внешних сил, действующих по одну сторону от сечения, на ось стержня и она заменяет действие отброшенной части на оставшуюся.

Эпюра продольных сил – это график, показывающий закон изменения продольной силы в поперечных сечениях вдоль его оси.

Пример построения эпюры продольных сил «N»

На вертикальный стержень действуют две силы в точке А и точке С.

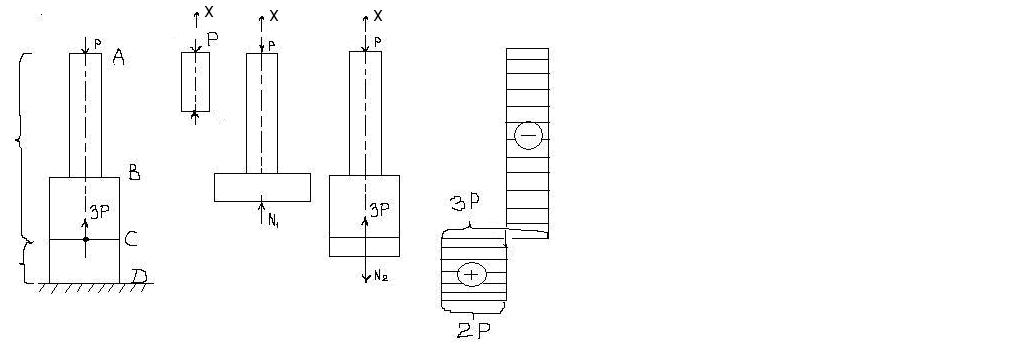
Порядок построения эпюры N

1. Разбиваем стержень на участии в пределах, которых продольная сила изменяется по одному и тому же закону. Границами участков являются точки приложения сосредоточенных сил и места начала и конца распределенной нагрузки. Следовательно, у нас первый участок от точки А до точки С, второй участок от точки С до точки D.

2. Определяем величину продольной силы на каждом из участков, используя метод сечений.

Участок 1.

N₁=P (сжатие)

Участок 2.

ΣХ=0 -Р+3Р-N₂=0 N₂=2P (растяжение)

Вывод: Там где приложена сосредоточенная сила, на эпюре N имеется скачок, равный величине этой силы.

Напряжения при растяжении (сжатии)

Возьмем стержень, нанесем на поверхность линии и приложим силы Р.

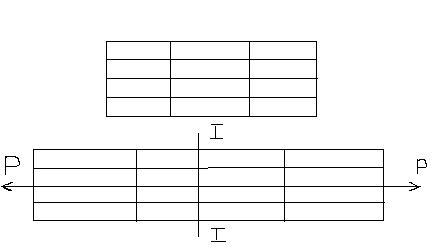
Из опыта видно: поперечные сечения плоские до деформации остаются плоскими и перпендикулярными оси стержня после деформации. Это явление обнаружено Бернулли и носит название гипотезы плоских сечений или гипотезы Бернулли.

Якоб Бернулли (17 век) старший в талантливой семье швейцарских ученых. Он был математиком, физиком, механиком.

На основании гипотезы Бернулли можно утверждать, что нормальное напряжение в сечении I – I постоянно.

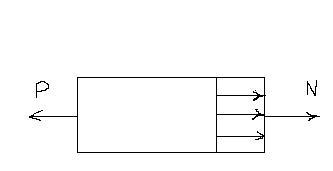
Запишем интегральную зависимость, т.е. просуммируем по сечению

N=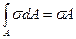

где, А – площадь поперечного сечения.

Следовательно

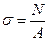(1) растяжение (+); сжатие (-).

Условие прочности при растяжение (сжатии)

Максимальные напряжения, возникающие в стержне при растяжении (сжатии) не должны превышать допускаемых напряжений для материала

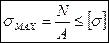(2)

Используя условие прочности (2) можно решать следующие задачи:

1. Выполнять проверочный расчет, т.е. по известной продольной силе и размерам поперечного сечения определять фактические напряжения в стержне и сравнивать их с допускаемыми.

2. Выполнять проектировочный расчет, т.е. по известной продольной силе и [σ] можно производить подбор сечений – определять их размеры.

.

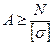3. Определить допускаемую нагрузку по известным размерам поперечного сечения и [σ]

N_доп = [σ]×А.

Деформации при растяжении – сжатии

Рассмотрим стержень, загруженный на конце силой Р. Под действием приложенной силы стержень деформируется. Удлиняется, а поперечное сечение уменьшается.

Введем понятия:

Δℓ=ℓ₁ - ℓ - абсолютное удлинение (укорочение) бруса;

Δa=a₁ – a – абсолютное сужение поперечного сечения в направлении размера «а»;

Δb=b₁ – b – абсолютное сужение поперечного сечения в направлении размера «b»;

ε= 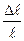относительная линейная (продольная) деформация (безразмерная величина);

εⁱ_a= 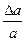- относительная поперечная деформация в направлениях размера а;

εⁱ_b= - относительная поперечная деформация в направлениях размера b;

Для изотропного материала εⁱ_a = εⁱ_b= εⁱ

Для анизотропного материала εⁱ_а ≠ εⁱ_b

Отношение относительной поперечной деформации к относительной продольной деформации называется коэффициентом поперечной деформации или коэффициентом Пуассона. (Симон Дени Пуассон – французский механик, математик, 19 век)

(3)

Для всех материалов µ=0..0,5

Сталь µ=0,24 – 0,3.

Медь µ=0,31 – 0,34.

Чугун µ=0,23 – 0,32.

Резина µ=0,5.

Пробка µ=0.

Коэффициент Пуассона характеризует способность материала к поперечной деформации.

Закон Гука

Опытным путем установлено, что между нагрузкой и деформацией бруса существует прямая пропорциональность до определенного предела, эта зависимость носит название закона Гука.

σ=Еε (4)

где Е – модуль продольной упругости материала. Это физическая постоянная материала, которая определяется опытным путем. Иногда Е называют модулем I рода или модулем Юнга (Томас Юнг – английский физик, врач, астроном 19 век)

Сталь: Е =200 ГПа, Г=10⁹.

Медь: Е = 100 ГПа.

Алюминий: Е =70 ГПа.

Дерево (сосна): Е=10 ГПа.

Модуль Юнга характеризует способность материала сопротивляется упругим деформациям.

Определение перемещений при растяжении – сжатии

Ранее определили напряжения и деформации

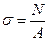, ε= 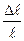, подставив эти соотношения в формулу (4)

,

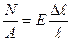получаем закон Гука в развернутой форме при осевом растяжении – сжатии

(5)

при N=const, А=const,

где EА – жесткость сечения при растяжении.

Для бруса у которого N и А изменяются по длине по непрерывному закону абсолютное удлинение Δℓ определяется по формуле

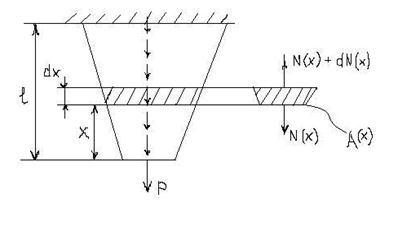
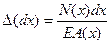
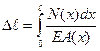
Дата добавления: 2014-01-07