
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Механические колебания и волны
|
|
|
|
Лекция 3.
Механические колебания: гармонические, затухающие, вынужденные. Резонанс. Автоколебания. Энергия гармонических колебаний. Разложение колебаний в гармонический спектр. Применение гармонического анализа для обработки диагностических данных. Механические волны, их виды и скорость распространения. Уравнение волны. Энергетические характеристики волны. Эффект Доплера и его применение для неинвазивного измерения скорости кровотока.
Повторяющиеся движения или изменения состояния называют колебаниями (переменный электрический ток, движение маятника, работа сердца и т. п.). Всем колебаниям, независимо от их природы, присущи некоторые общие закономерности. В зависимости от характера взаимодействия колеблющейся системы с окружающими телами различают колебания свободные, вынужденные и автоколебания. Колебания распространяются в среде в виде волн.
Свободными (собственными) колебаниями называют такие, которые совершаются без внешних воздействий за счет первоначально полученной телом энергии. Характерными моделями таких механических колебаний являются материальная точка на пружине (пружинный маятник) и материальная точка на нерастяжимой нити (математический маятник).
В этих примерах колебания возникают либо за счет первоначальной потенциальной энергии (отклонение материальной точки от положения равновесия и движение без начальной скорости), либо за счет кинетической (телу сообщается скорость в начальном положении равновесия), либо за счет и той и другой энергии (сообщение скорости телу, отклоненному от положения равновесия).
Пружинный маятник
 В положении равно-весия упругая сила
В положении равно-весия упругая сила  уравновешивает силу тяжести уравновешивает силу тяжести  . .
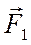 = = Если оттянуть пружи-ну на х, то на мат. точку будет действо-вать большая упругая сила.
F = -kx, (закон Гука)
где k - коэффициент пропорциональности между силой и смеще-нием, который являет-ся жесткостью пружи-ны. Знак минус показывает, что сила всегда направлена в сторону положения равновесия: F < 0 при
х > 0, F > 0 при х < 0.
Если оттянуть пружи-ну на х, то на мат. точку будет действо-вать большая упругая сила.
F = -kx, (закон Гука)
где k - коэффициент пропорциональности между силой и смеще-нием, который являет-ся жесткостью пружи-ны. Знак минус показывает, что сила всегда направлена в сторону положения равновесия: F < 0 при
х > 0, F > 0 при х < 0.
| Математич-ий маятник
 отклонен от равнове-сия на угол α, что считаем траекторию движения мат. точки прямой линией, совпа-дающей с осью ОХ. При этом:
отклонен от равнове-сия на угол α, что считаем траекторию движения мат. точки прямой линией, совпа-дающей с осью ОХ. При этом:
 где х - смещение мат. точки от положения равновесия, l - длина нити маятника.
На мат. точку действуют сила натя-жения
где х - смещение мат. точки от положения равновесия, l - длина нити маятника.
На мат. точку действуют сила натя-жения  сила тяжести сила тяжести  , модуль ра-внодействующей равен , модуль ра-внодействующей равен
 где k - коэффициент пропорциональности между силой и смещением, равен
где k - коэффициент пропорциональности между силой и смещением, равен 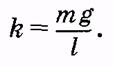 .
Силы, неупругие по природе, но аналогич-ные силам, возникаю-щим при деформациях упругих тел, называ-ют квазиупругими .
Силы, неупругие по природе, но аналогич-ные силам, возникаю-щим при деформациях упругих тел, называ-ют квазиупругими
|
На мат. точки, в этих примерах, кроме упругой и квазиупругой силы действует и сила сопротивления (трения), модуль которой обозначим Fc, тогда
F=-kx+Fc
Дифференциальное уравнение, описывающее движение мат. точки, получаем на основании второго закона Ньютона (произведение массы тела на его ускорение равно сумме всех действующих сил):
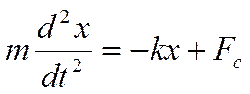
Незатухающие
колебания
модель, сила (Fc = 0). имеем:
 . Заменяя . Заменяя
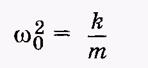 получаем диф. уравнение второго порядка: получаем диф. уравнение второго порядка:
 решение, приводит к гармоническому колебанию:
решение, приводит к гармоническому колебанию:
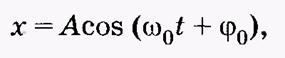 где
где 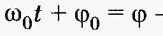 фаза колебаний.
j0 - начальная фаза (при t = 0),
w0 — круговая частота колебаний, А - их амплитуда в момент t = 0.
Среди различных видов колебаний гармоническое колебание является наиболее простой формой.
Величина фаза колебаний.
j0 - начальная фаза (при t = 0),
w0 — круговая частота колебаний, А - их амплитуда в момент t = 0.
Среди различных видов колебаний гармоническое колебание является наиболее простой формой.
Величина 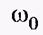 имеет важный физический смысл, так как определяет частоту колебаний имеет важный физический смысл, так как определяет частоту колебаний  Период колебаний
Период колебаний
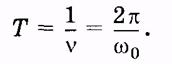 период колебаний пружинного маятника период колебаний пружинного маятника
 период колебаний мат. маятника
период колебаний мат. маятника
 скорость мат. точки при гармоническом колебании, есть производная от
скорость мат. точки при гармоническом колебании, есть производная от
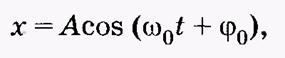 по времени: по времени:
 преобразуем
преобразуем
 Сравнивая х и v, замечаем, что фаза скорости на
Сравнивая х и v, замечаем, что фаза скорости на больше фазы смещения, т. е. скорость опережает по фазе смещение на больше фазы смещения, т. е. скорость опережает по фазе смещение на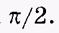 Продифференцировав v, найдем ускорение:
Продифференцировав v, найдем ускорение:
 где
где - ампли-туда ускорения.
преобразуем - ампли-туда ускорения.
преобразуем
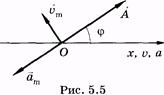
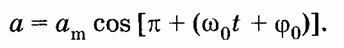 Из сравнения a и x следует, что фазы ускорения и смещения различаются на π, т. е. эти величины изменяются в противофазе. Графики зависимости смещения, скорости и ускорения от времени показаны на рис. 5.4, а их векторные диаграммы — на рис. 5.5.
Из сравнения a и x следует, что фазы ускорения и смещения различаются на π, т. е. эти величины изменяются в противофазе. Графики зависимости смещения, скорости и ускорения от времени показаны на рис. 5.4, а их векторные диаграммы — на рис. 5.5.

| Затухающие колебания.
При наличии силы со-противления (трения)
 , где r — коэффициент трения (сопротивления),
колебания становятся затухающими. , где r — коэффициент трения (сопротивления),
колебания становятся затухающими.
 Диф уравнение имеет вид Диф уравнение имеет вид
 Разделив на т, запишем его в форме:
Разделив на т, запишем его в форме:
 После замены После замены  и и 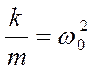 получаем: получаем:
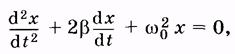 где b - коэффициент затухания, w0- круговая частота собственных колебаний системы (без затухания).
Решение зависит от знака
где b - коэффициент затухания, w0- круговая частота собственных колебаний системы (без затухания).
Решение зависит от знака  , где w - круговая частота затухающих колебаний. При w2 - b2 > 0 круговая частота w действительная величи-на и решение будет следующим: , где w - круговая частота затухающих колебаний. При w2 - b2 > 0 круговая частота w действительная величи-на и решение будет следующим:

 изменение амплитуды:
изменение амплитуды:
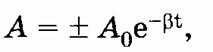 где значение А 0 приведено на рисунке.
Период затухающих колебаний определяется формулой:
где значение А 0 приведено на рисунке.
Период затухающих колебаний определяется формулой:
 При малом трении
При малом трении
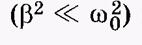 период затухающего колебания близок к периоду незатухающего свобод-ного колебания: период затухающего колебания близок к периоду незатухающего свобод-ного колебания: Быстрота убывания амплитуды колебаний определяется коэффи-циентом затухания: чем сильнее тормозящее де-йствие среды, тем боль-ше b и тем быстрее уменьшается амплиту-да. Степень затухания характеризуют логарифмическим дек-рементом затухания,, равную натуральному логарифму отношения двух последовательных амплитуд, разделенных интервалом времени, равным периоду колебаний.
Быстрота убывания амплитуды колебаний определяется коэффи-циентом затухания: чем сильнее тормозящее де-йствие среды, тем боль-ше b и тем быстрее уменьшается амплиту-да. Степень затухания характеризуют логарифмическим дек-рементом затухания,, равную натуральному логарифму отношения двух последовательных амплитуд, разделенных интервалом времени, равным периоду колебаний.
 коэффициент затухания и логарифмический декремент затухания связа-ны простой зависимо-стью:
коэффициент затухания и логарифмический декремент затухания связа-ны простой зависимо-стью: При сильном затухании (b2 > w2) период колебания является мнимой величиной. Движение в этом случае уже не будет периодическим и называется апериодическим.
При сильном затухании (b2 > w2) период колебания является мнимой величиной. Движение в этом случае уже не будет периодическим и называется апериодическим.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 345; Нарушение авторских прав?; Мы поможем в написании вашей работы!