Качение одиночного колеса с эластичной шиной по деформируемому грунту

Полемика реализма и номинализма

Схоластика

Главным направлением в развитии средневековой философии феодального общества была схоластика.

1) Центральным вопросом, которым занимались схоластики, был вопрос об отношении знания к вере.

Схоластики исходили из тезиса о первенстве и главенстве веры над разумом (Ф.Аквинский).

2) Другой (философский) вопрос – отношение общего к единичному (реализм и номинализм).

Реализм ( Ф.Аквинский) - учение, согласно которому подлинной реальностью обладают только общие понятия (универсалии), а не единичные предметы, существующие в эмпирическом мире.

Универсалии существуют до вещей! (Платон)

П ротивоположное реализму направление носило название номинализма.

Номинализм (И.Росцеллин, Д.Скотт, В.Оккам) – философское учение, отрицающее онтологическое значение общих понятий и утверждающее, что они существуют не в действительности, а только в мышлении. По утверждению номиналистов, общие понятия – это только имена, они не обладают никаким самостоятельным существованием вне и помимо единичным вещей.

Универсалии существуют после вещей! (материализм)

3.1. Основные предпосылки, принимаемые при рассмотрении качения колеса по деформируемому грунту

При движении по грунту параметры качения колеса существенно зависят от характеристик грунтовой поверхности. Большинство предлагаемых исследователя­ми зависимостей по их определению имеют сложную структуру, поскольку авторы стремятся как можно точнее учесть все характеристики грунта. К таким характери­стикам относятся, например, угол внутреннего трения грунта, коэффициент моле­кулярных и капиллярных сил сцепления, коэффициент трения, модуль среза, коэф­фициент постели, а также большое количество эмпирических коэффициентов, учи­тывающих различное состояние грунта.

Для определения этих характеристик требуется проведение достаточно тру­доемких экспериментов. Практическая ценность уравнений, в которые входит большое число таких эмпирических показателей и характеристик, в существенной мере снижается, а достоверность получаемых результатов вызывает определенное сомнение вследствие неизбежности принятия при выводе зависимостей определен­ных допущений.

По нашему мнению, такой путь анализа процесса качения колеса по грунту малопригоден для изучения распределения потока мощности по отдельным состав­ляющим, потому что многообразие грунтов (вернее, их характеристик) и их зави­симость от погодных условий и даже от времени суток обусловливают практиче­скую невозможность учета конкретных текущих характеристик различных грунтов.

При рассмотрении процесса качения колеса по грунту воспользуемся ранее принятым в механике грунтов выражением для определения зависимости удельно­го давления q сопротивления вдавливанию в грунт штампа от глубины его погру­жения h:

q = ch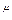, (3.1)

где: с - параметр, характеризующий начальное сопротивление грунта вдавливанию штампа;

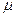- показатель степени, характеризующий закон изменения сопротивления грунта вдавливанию.

Эту формулу широко используют для построения зависимостей, характери­зующих процесс качения колеса по грунту. Преимущество уравнения (1) заклю­чается, прежде всего, в его относительной простоте и наличии экспериментальных данных для определения величин с и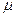. Основным его недостатком является обна­руженная рядом исследователей зависимость величин с и 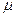от формы и размеров штампа, что снижает точность расчетов, проведенных на основе использования табличных значений с и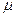. Однако достоверность расчетов можно в значительной степени повысить, если экспериментально определять эти величины путем прока­тывания по грунту колеса соответствующих габаритных размеров.

Табличные значения с и 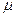, приведенные в многочисленных работах, с успе­хом используются для решения ряда практических задач. В частности, сравнительные расчетные исследования колес с приблизительно равными геометрическими размерами дают вполне удовлетворительное совпадение результатов расчетов с ре­зультатами экспериментов.

Степенная зависимость вполне применима при проведении исследований полноприводных автомобилей народнохозяйственного назначения, движение кото­рых, в основном, осуществляется по грунтовым дорогам и сельскохозяйственным грунтовым фонам.

При исследованиях колесной техники, имеющей специальное назначение и используемой часто в специфических условиях движения, более достоверны зави­симости для оценки деформации грунта, учитывающие его неоднородность и раз­личные комбинации прочности слоев грунта [1]. Эти зависимости более сложные, требуют большего количества характеристик грунта, но более точно отражают фи­зические процессы при движении колесных машин.

Степенная зависимость и зависимости, в основе которых лежат такие пара­метры, как модуль деформации грунта Е и несущая способность грунта Р_S, связы­ваются аналитическими выражениями, позволяющими осуществить переход от формулы (3.1) к выражениям для Е и Р_S в формулах Я.С. Агейкина.

3.2. Уравнения силового равновесия колеса при его качении по грунту

Рассмотрим прямолинейное качение одиночного эластичного колеса по де­формируемому грунту, приняв при этом некоторые допущения:

- рассматривается прямолинейное движение с установившейся небольшой
скоростью;

- грунт однороден, имеет одинаковые физико-механические свойства;

- поверхность грунтового основания горизонтальная и ровная;

- упругость грунта мала, и ею можно пренебречь.

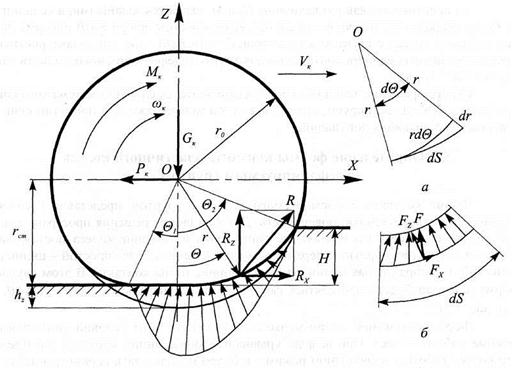
Введем полярную систему координат, совместив центр координат (точка О) с осью колеса. Расчетная схема приведена на рис. 3.1.

Задача рассматривается как двумерная. Двухмерность задачи понимается в том смысле, что все существенные силы взаимодействия колеса с грунтом лежат в плоскости вращения колеса.

В общем случае качения эластичного колеса по деформируемому грунту форма поверхности колеса в контакте с грунтом задается уравнением:

r = f(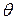), (3.2)

где: 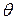- полярный угол, отсчитываемый от вертикальной оси Z;

r - величина радиус-вектора, проведенного из точки О к данной точке по­верхности колеса.

Обозначим погонную нагрузку, действующую на элементарный участок длины дуги колеса dS, через F [Н/м], которую можно разложить по осям X и Z на компоненты (F_x и F_z).

Элементарный участок длины дуги колеса dS выразим через угол 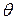и ради­ус-вектор r. Из схемы деформации элемента колеса (рис. 3.1, а) имеем:

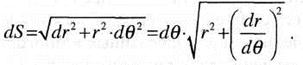
Рис. 3.1. Расчетная схема качения эластичного колеса по деформируемому грунту: а -деформация элемента колеса; б - нагрузка на элементарный участок дуги колеса

Элементарную силу, действующую на дугу колеса длиной dS можно пред­ставить в виде FdS [Н] (рис. 3.1, б). Она возникает как равнодействующая эле­ментарных сил смятия грунта, сил трения и сил, возникающих при деформации ко­леса. Далее, разлагая элементарную силу по осям X и Z на компоненты и интегри­руя по дуге контакта X и Z

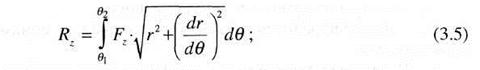
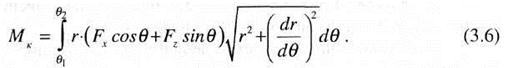
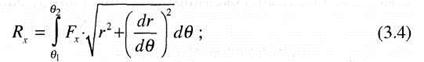
на компоненты и интегри­руя по дуге контакта поверхности колеса с грунтом, запишем уравнения равновесия колеса в виде:

Поскольку из уравнений силового равновесия колеса вытекает:

R_x = P_k (3.7)

R_z = G_k (3.8)

то, зная зависимости F (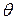) и r (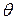), по соотношениям (3.4)-(3.6) можно определить величины Р_к; G_K и М_к.

На практике же, как раз величины G_k и М_к являются заданными, а величину Р_к можно определить только в том случае, если известны эпюра F (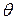) и форма ли­нии контакта колеса с грунтом в виде зависимости r (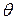), Обе эти характеристики зависят от сцепных свойств контакта «шина-грунт» и деформационных свойств как грунта, так и шины.

Строгое решение такой обратной задачи является сложной математической проблемой. Проиллюстрируем, сколь сложна эта задача даже при принятии суще­ственных упрощающих допущений.

3.3. Определение формы контакта эластичного колеса с деформируемым грунтом

Форма контакта деформируемого колеса с грунтом представляет собой сложную пространственную поверхность. Для упрощения решения пространствен­ной задачи полагаем, что контактные напряжения по ширине колеса постоянны. Тогда сложную трехмерную поверхность можно заменить более простой - цилинд­рической, где образующая цилиндра равна ширине пятна контакта. В этом случае форма контакта будет определяться формой дуги с центральным углом (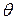₁ + 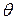₂) (см. рис. 3.1).

Форма контактной линии меняется в зависимости от условий движения и режима работы колеса. При выводе уравнения формы линии контакта полагаем, что колесо работает в свободном режиме, и будем использовать параметры дефор­мационных характеристик шины и грунта.

Для твердой опорной поверхности зависимость прогиба шины h_z от нор­мальной нагрузки G,- близка к линейной:

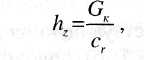
где с_г - радиальная жесткость шины (Н/мм).

Экспериментально установлено, что основным фактором, оказывающим влияние на изменение радиальной жесткости шины, является внутреннее давление воздуха в шине, и эта зависимость с достаточной для практических целей точно­стью может быть аппроксимирована линейной функцией:

(3.10)

где: K_pw - эмпирический коэффициент;

p_w - внутреннее давление воздуха в шине;

c_w - значение радиальной жесткости шины при минимальном внутреннем дав­лении воздуха.

В качестве примера на рис. 3.2 представлена экспериментальная зависи­мость c_r=f(p _w) для шины 16.00-20 модели И-159.

Для более точных расчетов зависимость (3.10) аппроксимируется уравнени­ем регрессии:

(3.11)

Коэффициенты уравнения регрессии К₁, К₂ и К₃ по отечественным шинам регулируемого давления представлены в табл. 3.1. Приведенные значения этих коэффициентов соответствуют номинальному внутреннему давлению воздуха в шине.

Рис. 3.2. Экспериментальная зависимость с. =f{p_w) для шины 16.00-20 модели И-159. Вер­тикальная нагрузка на колесе:

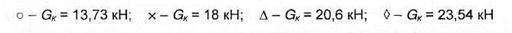
В табл. 3.1 В - ширина шины; r₀ - радиус шины при номинальном давле­нии; V г - габаритный объем шины, К_н - коэффициент насыщенности рисунка про­тектора, p_{w min} - минимально допустимое внутреннее давление воздуха в шине, f _0шн - коэффициент сопротивления качению прогретых шин при скорости 10 км/ч.

Из уравнений (3.9) и (3.10) получим:

Прогиб шины h_z гр при качении колеса по деформируемому грунту можно определить, исходя из схемы контакта колеса (см. рис. 3.1), полагая, что линия кс такта колеса с грунтом имеет плоскую и криволинейные зоны.

Часть вертикальной нагрузки, воспринимаемой плоской зоной контакта, (определится, как:

(3.13)

Связь между деформационными характеристиками колеса и грунта в пло­ской зоне контакта определится из соотношения:

c_r h_{z гр} =c F_ш H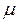 (3.14)

где: F_ш - площадь плоской зоны контакта шины с грунтом;

Н - глубина колеи, образуемая колесом, определяемая по выражению (3.71), вывод которого представлен ниже.

Таблица 3.1

Данные по отечественным шинам регулируемого давления

Шины	r0 /B	Vr,	Kн	Pw min, МПа	Номинальные значения	Коэффициенты регрессии
модель	м/м	дм^3			G k кН	pwн min	f0 шн	K1	к2	Кз
12.00-18, К-70-1	0,542/ 0,26		0,449	0,05	18,13	0,30	0,015		1,8	0,105
12.00R-18, КИ-115	0,542/ 0,26		0,427	0,08	18,13	0,45	0,012		2,4	0,070
12.00-20, М-93	0,571/ 0,27		0,367	0,05	18,13	0,30	0,015		2,9	0,040
12.00R-20, КИ-113	0,571/ 0,27		0,367	0,08	19,60	0,45	0,013		2,4	0,070
14.00-20, ОИ-25	0,63/ 0,32		0,358	0,05	24,50	0,32	0,017		4,9	0,030
14.00-20, ОИ-52	0,63/ 0,32		0,358	0,05	24,50	0,32	0,016		4,6	0,055
1220x400-533, ИП-184	0,60/ 0,34		0,348	0,05	25,58	0,32	0,016		3,7	0,070
425/85R21, Кама-1260	0,63/ 0,375		0,374	0,10	29,40	0,45	0,012		2,9	0,021
1200x500-508, ИД-П284	0,592/ 0,40		0,435	0,08	32,34	0,40	0,015		3,0	0,105
1300x530-533, ВИД-201	0,65/ 0,44		0,465	0,08	35,28	0,35	0,017		1,7	0,080

Введем допущения для рассматриваемой формы контакта деформируемого колеса с грунтом:

1) вне зоны контакта с опорной поверхностью колесо не испытывает деформации в радиальном направлении, поэтому в точке входа элемента колеса в контакт радиус колеса принимаем равным радиусу колеса в свободном состоянии го;

2) при выходе колеса из зоны контакта с опорной поверхностью оно не может мгновенно восстановить своей формы до состояния го, поэтому при в = 0₁ радиус-вектор колеса определяется зависимостью (3.2);

3) для упрощения вывода математического выражения линии контакта эластичного колеса с деформируемым грунтом примем, что вертикальная проекция центра колеса располагается в плоской зоне контакта. Тогда условный статический радиус колеса будет равняться:

r_ст = r₀ - h_z (3.15)

Уравнения (3.17) и (3.20) позволяют описать разные по форме контактные линии. Линия контакта деформируемого колеса с грунтом согласно исследованиям, приведенным в работе [1], в зависимости от сочетания нормальной нагрузки и дав­ления воздуха в шине, может принимать форму, близкую к окружности, либо фор­му с плоской нижней частью.

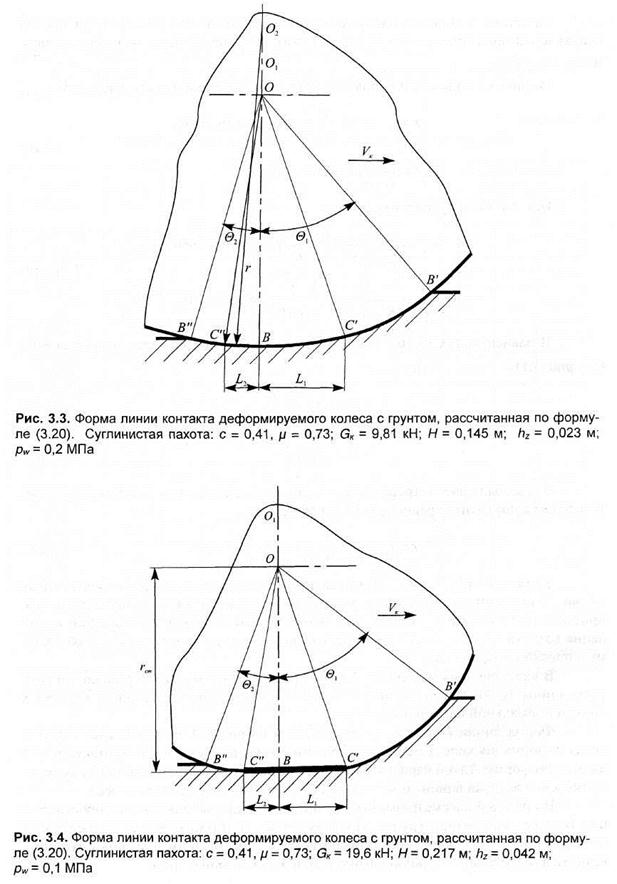
В качестве примера на рис. 3.3, 3.4 приведены расчетные формы линии кон­такта шины 16.00-20 при различных сочетаниях внутреннего давления воздуха в шине и нормальной нагрузки на колесо.

Форма линии контакта, представленная на рис. 3.3, соответствует случаю, когда деформация колеса меньше деформации грунта. Тогда линия контакта имеет выпуклую форму. Такой вариант формы контакта возможен при сочетании высоко­го давления воздуха в шине и небольших или средних нагрузках на колесо.

На рис. 3.4 рассматривается случай, когда деформация колеса сопоставима или больше деформации грунта. Поэтому линия контакта имеет в нижней части плоскую зону. Такая форма контакта соответствует небольшим значениям давления воздуха в шине и вертикальной нагрузке, близкой к номинальной.

Результаты расчетов хорошо соотносятся с формами линий контакта, при­водимыми в работах других авторов, и с наблюдаемыми при экспериментах. Таким образом, уравнения (3.17) и (3.20) позволяют учесть влияние внутреннего давления воздуха в шине и нормальной нагрузки на колесо на форму контакта при его взаи­модействии с грунтом.

Дата добавления: 2014-01-07