Связи и опорные устройства

Для соединения отдельных частей конструкции между собой и передачи внешней нагрузки на основание на нее накладываются связи, ограничивающие перемещения тех точек сооружения, к которым они приложены. Связи могут ограничивать либо повороты точек сооружения, либо их линейные смещения, либо и то и другое.

Основным видом связей в расчетной схеме является шарнирная связь.

Простой шарнир (рис. 1.2) накладывает две связи.

Рис. 1.2

В расчетную схему входит основание, т.е. тело, на котоpое опирается cистема в целом, считающееся неподвижной.

Неподвижность расчетной схемы относительно основания обеспечивается опорными связями (опорами).

Все опорные связи условно делятся на три основных типа:

- Подвижная шарнирная опора (рис.1.3, а). Такая опора не препятствует вращению конца бруса и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через ось катка (R).

- Неподвижная шарнирная опора (рис.1.3, б). Такая опора допускает вращение конца бруса, но устраняет поступательное движение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие, одна из которых направлена вдоль оси бруса (Н), другая - перпендикулярно к оси бруса (R).

- Жесткая заделка или защемление (рис.1.3, в). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре в общем случае может возникать реакция, которую обычно раскладывают на две составляющие (H и R) и момент защемления (М).

При рассмотрении реального объекта в число внешних сил включаются не только заданные нагрузки, но и реакции связей (опор), дополняющие систему сил до равновесного состояния.

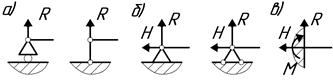
Рис. 1.3

Вопрос 2. Метод сечений.

Внутри любого материала имеются внутренние межатомные силы, наличие которых определяет способность тела воспринимать действующие на него внешние силы, сопротивляться разрушению, изменению формы и размеров. Приложение к телу внешней нагрузки вызывает изменение (увеличение или уменьшение) внутренних сил, т. е. появление дополнительных внутренних сил. В сопротивлении материалов изучаются дополнительные внутренние силы. Поэтому под внутренними силами (или внутренними усилиями) в сопротивлении материалов понимают силы взаимодействия между отдельными элементами сооружения или между отдельными частями элемента, возникающие под действием внешних сил.

Рассмотрим общий прием определения внутренних усилий, называемый методом сечений.

Рассечем стержень (рис. 2.3, а) плоскостью /, совпадающей с поперечным сечением стержня. В полученном поперечном сечении в общем случае действует шесть внутренних усилий: N, Q_Z, Q_Y, М_К, М_Z и Му (рис. 2.3, б,в).

Правая часть стержня (рис 2.3, в) находится в равновесии; значит, внешние силы Р₄ и Р₅, приложенные к ней, уравновешиваются внутренними усилиями, действующими на правую часть. Но те же внешние силы уравновешиваются и нагрузками, приложенными к левой части стержня (силами Р₁ , Р₂, Рз), так как весь стержень в целом (рис 2.3, а) также находится в равновесии. Следовательно, нагрузки, приложенные к левой части стержня (силы Р₁ , Р₂, Рз), и внутренние усилия, действующие на правую часть, статически эквивалентны друг другу.

Рис. 2.3

Таким образом, проекция на какую-либо ось внутренних усилий в сечении, действующих со стороны левой части стержня на правую, равна проекции на эту ось всех внешних сил, приложенных к левой части. Аналогично, момент относительно какой-либо оси внутренних усилий в сечении, действующих со стороны левой части стержня на правую, равен моменту всех внешних сил, приложенных к левой части относительно этой оси.

Из шести внутренних усилий, действующих в поперечном сечении стержня, проекции пяти усилий на каждую из осей х, у, и z равны нулю. Аналогично равны нулю и моменты пяти внутренних усилий относительно каждой из указанных осей. Это позволяет легко определять внутренние усилия в стержне, проецируя на ось х, или у, или z все внутренние усилия, действующие на правую часть стержня (рис. 2.3, в), и все внешние силы, приложенные к левой части (рис. 2.3, б), или определяя их моменты относительно одной из указанных осей.

Определим, например, величину продольной силы N в поперечном сечении I, показанном на рис. 2.3. Из рис. 2.3, в видно, что проекция на ось х всех внутренних усилий, действующих на правую часть стержня, равна +N, если для проекций положительным считать направление справа налево. Поэтому сила N равна сумме проекций на ось х всех внешних сил, действующих на левую часть стержня (т. е. сил Р₁ , Р₂, Рз – см. рис. 2.3, б). Аналогично значение, например, крутящего момента М_К в поперечном сечении стержня равно сумме моментов сил Р₁ , Р₂, Рз (рис. 2.3, б) относительно оси х, если положительными считать моменты, направленные по часовой стрелке (при взгляде с левого конца оси х на правый) и т. д.

Внутренние силы, действующие в сечении со стороны левой части на правую, можно определить по внешним силам, приложенным не к левой, а к правой части. В этом случае полученные направления проекций внешних сил на выбранные оси и моментов относительно этих осей необходимо изменять на противоположные.

Вопрос 3. Центральное растяжение-сжатие.

Центральным растяжением (или центральным сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние усилия (поперечные силы, изгибающие моменты и крутящий момент) равны нулю. Иногда центральное растяжение (или центральное сжатие) кратко называют растяжением (или сжатием).

На рис. 1.2, а изображен прямой брус, закрепленный одним концом и нагруженный на другом конце силой Р, направленной вдоль его оси.

Во всех поперечных сечениях этого бруса возникают только продольные растягивающие силу, и, следовательно, такой брус по всей длине является центрально растянутым. При противоположно направленной силе Р (рис, 1.2, б) брус по всей длине испытывает сжатие.

Растягивающие продольные силы принято считать положительными, а сжимающие – отрицательными.

Рис. 2.2

На рис. 2.2, а изображен брус, нагруженный силами Р₁ и Р₂, направленными вдоль его оси, двумя силами Р₃, параллельными оси и приложенными на равных расстояниях от нее в поперечном сечении с, а также двумя силами Р₄, направленными под углом а к оси бруса, и приложенными в поперечном сечении d на равных расстояниях от оси.

На рис. 2.2, б изображена расчетная схема, полученная путем замены бруса его осью и переноса внешних нагрузок к этой оси.

Силы Р₁ и Р₂ на расчетной схеме действуют вдоль оси бруса; силы Р₃ и силы Р₄, показанные на рис, 2.2, а, приводятся соответственно к силам 2Р₃ и 2P₄ cos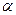, также направленным вдоль оси. Таким образом, на расчетной схеме (рис. 2.2, б) все внешние силы действуют вдоль оси бруса. Следовательно, в поперечных сечениях рассматриваемого бруса возникают только продольные силы. Определим в качестве примера продольную силу N, в сечении / — / (см. рис. 2.2, б). На рис. 2.2, в, г показаны продольные силы N, действующие на левую (по отношению к сечению / — /) и на правую части бруса. Направления этих сил приняты в предположении, что они являются растягивающими (т. е. положительными). Если в результате расчета значение N получится со знаком «минус», то это будет означать, что в действительности брус в сечении / — / сжат.

Для определения силы N воспользуемся методом сечений. Составим уравнение равновесия в виде суммы проекций на ось бруса всех сил, действующих на левую его часть (см. рис. 2.2, в):

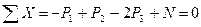
откуда

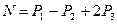
Этот же результат можно получить, и не составляя уравнения равновесия, а используя то положение, что на основании метода сечений проекция внутренних сил на ось бруса (т. е. продольная: сила), действующих со стороны левой его части на правую, равна сумме проекций на эту же ось всех внешних сил, прило­женных к левой части. Следовательно,

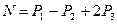
Силы Р₁ и 2Р₃ взяты со знаком «плюс», потому что их направление совпадает с положительным направлением силы N_/ действующей на правую часть бруса.

Аналогично найдем продольные силы в сечениях //—//, III—III, IV — IV (рис. 2.2, б), проецируя силы, приложенные слева от этих сечений, на ось бруса:

; ;

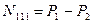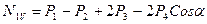
Очевидно, что на всем участке аЬ (между точками приложения сил Р₁ и Р₂) продольная сила постоянна и равна Р₁, аналогично и на других участках (между точками приложения внешних сил) продольные силы имеют постоянные значения.

Построим график, показывающий изменение продольных сил по длине оси бруса, называемый эпюрой продольных сил (эпюрой N). Для этого проведем ось эпюры ае, параллельную оси бруса (рис. 2.2, д), и перпендикулярно к ней отложим ординаты, изображающие в некотором масштабе величины продольных сил в поперечных сечениях бруса. Полученную таким путем эпюру принято штриховать (так же как и эпюры других внутренних усилий, рассматриваемые в последующих главах курса) прямыми линиями, перпендикулярными к ее оси. Каждая такая линия в принятом масштабе дает величину продольной силы в соответствующем поперечном сечении бруса.

В поперечном сечении, в котором к брусу приложена сосредоточенная сила, не перпендикулярная к его оси, значение продольной силы изменяется скачкообразно: слева от этого сечения, продольная сила имеет одно, а справа — другое значение, отличающееся на величину проекции (на ось бруса) указанной сосредоточенной силы. В соответствии с этим эпюра, изображенная на рис. 2.2, д, имеет скачки (уступы) в точках а, Ь, с, d, e, равные соответственно величинам Р₁ — Р ₂, 2Р₃, — 2P₄cosa и значению реакции опорного закрепления бруса.

Для построения эпюр внутренних усилий, возникающих в поперечных сечениях бруса, нет необходимости изображать и брус с действующими на него нагрузками и расчетную схему, а достаточно привести один из этих чертежей. Точно так же нет необходимости изображать отдельные части бруса, на которые он расчленяется поперечными сечениями.

Например, для решения рассмотренной задачи можно изобразить лишь брус (рис. 2.2, а) или его расчетную схему (рис. 2.2, б), а также эпюру продольных сил N (рис. 2.2, д) и мысленно представить остальные схемы, приведенные на рис. 2.2.

При действии на брус внешней распределенной осевой (т. е. направленной вдоль оси бруса) нагрузки продольные силы на участке, на котором такая нагрузка приложена, изменяются непрерывно.

Вопрос 4. Определение внутренних усилий.

Рассмотрим элемент конструкции, на который действует система внешних сил, находящихся в равновесии (рис. 2.1, а). (Напоминаем, что в число внешних сил входят как заданные активные силы, так и реакции связей.) Мысленно рассечем элемент плоскостью I.

Рис. 2.1

Силы воздействия отсеченной правой части элемента на его левую часть (на правый ее торец) являются по отношению к ней внешними; для всего же элемента в целом они являются внутренними силами. Этим силам (на основании известного закона механики: действие равно противодействию) равны по величине и противоположны по направлению внутренние силы воздействия левой части элемента на правую.

В общем случае пространственной задачи взаимодействие между левой и правой частями элемента можно представить некоторой силой R, приложенной в произвольно выбранной точке О сечения I, и моментом М относительно некоторой оси, проходящей через эту точку (рис. 2.1, б, в). Сила R является главным вектором, а момент М — главным моментом системы внутренних сил, действующих по проведенному сечению.

Определение внутренних сил, возникающих в брусе, обычно производится для сечений, перпендикулярных к его продольной оси; т. е. для поперечных сечений бруса. Точка О принимается расположенной на оси бруса, т. е. совпадающей с центром тяжести его поперечного сечения. Главный вектор R раскладывается на две составляющие силы: силу N, направленную вдоль оси бруса и называемую продольной силой, и силу Т действующую в плоскости поперечного сечения и называемую поперечной силой (рис. 2.2, а).

Рис. 2.2

Момент М раскладывается на два составляющих момента: момент М_К, действующий в плоскости поперечного сечения и называемый крутящим моментом, и момент М_И действующий в плоскости, перпендикулярной к поперечному сечению, и называемый изгибающим моментом (рис. 2.2, б).

Каждому из внутренних усилий N, Т, М_К и М_И соответствует определенный вид деформации бруса, Продольной силе. N соответствует растяжение (или, сжатие), поперечной силе Т – сдвиг, крутящему моменту М_К – кручение, а изгибающему моменту М_И – изгиб. Различные их сочетания, например, сжатие с изгибом, изгиб с кручением и т. п., представляют собой сложные сопротивления. Внутренние усилия N и М_К характеризуются каждое одним параметром – величиной усилия. Поперечная сила Т характеризуется двумя параметрами, например, величиной этой силы и ее направлением (в плоскости поперечного сечения бруса). Более удобно силу Т определять через составляющие ее поперечные силы Q_Z и Q_Y, параллельные двум взаимно перпендикулярным осям, расположенным в плоскости поперечного сечения бруса (см, рис. 2.2, а). Изгибающий момент М_И также характеризуется двумя параметрами; его обычно раскладывают на два составляющих изгибающих момента М_Z и М_Y относительно осей z и у. Таким образом, взаимодействие любых двух частей конструкции характеризуется тремя составляющими N, Q_Z и Q_Y главного вектора и тремя составляющими М_К, М_Z и М_Y главного момента внутренних сил, возникающих, в рассматриваемом поперечном сечении. Эти составляющие называются внутренними силовыми факторами, или внутренними усилиями.

Заключительная часть: напомнить тему, цели занятий, ответить на поставленные вопросы, дать задание на самостоятельную работу, самоподготовку; выдать план проведения всех видов занятий

Задание для самостоятельной работы

Изучить: конспект лекции.

Задание на самоподготовку

1. Подготовиться к практическому занятию.

Изучить:

1. Суть метода сечений.

2. Центральное растяжение- сжатие.

Вопросы для самоконтроля

1. Что называют прочностью, жесткостью, устойчивостью детали?

2. Что такое сосредоточенная сила, распределенная нагрузка и момент?

3. Перечислите внутренние силовые факторы.

Разработал __________________________________________

(подпись, должность, фамилия, звание)

«____»______________20___года

Дата добавления: 2014-01-07