Условие независимости криволинейного интеграла второго рода от пути интегрирования на плоскости

В общем случае криволинейный интеграл 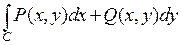, где кривая C соединяет точки A и B на плоскости XY, зависит от пути C. Выясним, каким условиям должны удовлетворять функци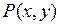и и 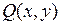в области 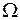, чтобы результат интегрирования по любой кривой, лежащей внутри 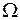, и соединяющей две фиксированные точки, был одинаковым.

Очевидно, что условие независимости результата интегрирования криволинейного интеграла по кривой, соединяющей две фиксированные точки области, от формы этой кривой равносильно условию равенства нулю интеграла по любой замкнутой кривой, лежащей в этой области. Действительно, обозначим через и 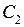две кривые, лежащие в 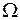, с общими начальной и конечной точками. Тогда кривая , где знак «-» означает, что соответствующая кривая проходится в противоположном направлении, будет замкнутой. Следовательно, соотношение

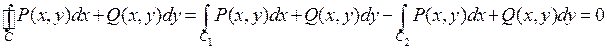
равносильно тому, что .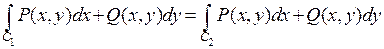

Итак, найдем условие на функци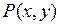и и 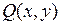, необходимое и достаточное для того, чтобы криволинейный интеграл 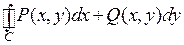, где C – произвольная замкнутая кривая, лежащая в 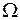, был равен нулю.

А. Докажем, что условие , выполняющееся всюду в 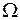для непрерывных функций 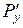и , является достаточным для того, чтобы криволинейный интеграл 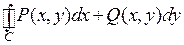по любой замкнутой кривой C, лежащей в 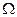, был нулем. Пусть C – замкнутая кривая без самопересечений. Тогда применим к интегралу 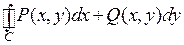формулу Грина и с использованием условия получим .

Пусть теперь C – самопересекающаяся кривая, Тогда, как показано на рисунке, кривая C разбивается точками самопересечения на конечное число фрагментов, которые

попарно соединяются в объединение нескольких замкнутых кривых без самопересечений. Применяя к интегралу по этим кривым формулу Грина, мы так же, как и выше, получим .

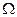Б. Докажем, что выполнение условия в для непрерывных функций 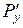и , является необходимым условием того, что для любой замкнутой лежащей в 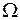кривой C. Предположим противное: пусть интеграл по любой замкнутой кривой равен нулю, но 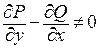в некоторой внутренней точке M области 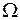. Допустим, в этой точке. В силу непрерывност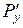и и существует окрестность точки M, лежащая в 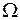, в которой также . Возьмем область D в этой окрестности с границей C. Согласно формуле Грина, примененной к кривой C и области D, 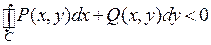, что противоречит предположению о том, что интеграл по любой замкнутой кривой в 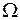равен нулю. Противоречие доказывает необходимость выполнения условия всюду в .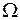

Дата добавления: 2014-01-07