
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способ вычисления поверхностного интеграла первого рода
|
|
|
|
Пусть требуется вычислить 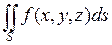 , когда функция
, когда функция  непрерывна на поверхности S. Поверхность S задана параметрически:
непрерывна на поверхности S. Поверхность S задана параметрически: 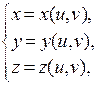
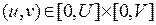 , где функции
, где функции 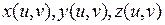 имеют непрерывные в прямоугольнике
имеют непрерывные в прямоугольнике  частные производные первого порядка. Разобьем прямоугольник значений параметров
частные производные первого порядка. Разобьем прямоугольник значений параметров  на прямоугольники
на прямоугольники 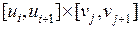 ,
,  . Соответственно такому разбиению прямоугольника параметров мы получим разбиение поверхности S на фрагменты
. Соответственно такому разбиению прямоугольника параметров мы получим разбиение поверхности S на фрагменты  . Как известно, площадь такого фрагмента может быть получена по формуле
. Как известно, площадь такого фрагмента может быть получена по формуле
 ,
,
и согласно интегральной теореме о среднем,
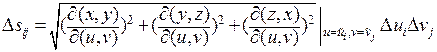
где 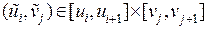 ,
,  ,
,  . Выберем теперь на поверхностном фрагменте
. Выберем теперь на поверхностном фрагменте  в качестве точки с координатами
в качестве точки с координатами 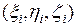 точку с координатами
точку с координатами 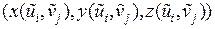 . Теперь так же, как в предыдущем параграфе, получим следующее выражение для поверхностного интеграла первого рода:
. Теперь так же, как в предыдущем параграфе, получим следующее выражение для поверхностного интеграла первого рода:
 .
.
Правая часть последнего выражения представляет собой интегральную сумму при интегрировании по прямоугольнику  , поэтому, переходя к пределу, получим
, поэтому, переходя к пределу, получим 
Заметим, что в плоскости изменения параметров может получиться не обязательно прямоугольник  , а другая, более сложная, область. В любом случае приведенная формула позволяет от интеграла по площади поверхности перейти к двойному интегралу по области значений параметров.
, а другая, более сложная, область. В любом случае приведенная формула позволяет от интеграла по площади поверхности перейти к двойному интегралу по области значений параметров.
П р и м е р ы.
1. Вычислить 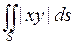 , где S – часть параболоида
, где S – часть параболоида  , отсекаемая плоскостью
, отсекаемая плоскостью  .
.
Р е ш е н и е. Прежде всего, заметим, что проекцией данной поверхности S на плоскость XOY является круг  . Параметризуем уравнение поверхности с помощью полярных координат:
. Параметризуем уравнение поверхности с помощью полярных координат:
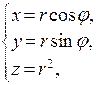
 .
.
Вычислим входящие в формулу якобианы:  .
.
Теперь получим представление исходного поверхностного интеграла через двойной интеграл по прямоугольнику значений параметров:
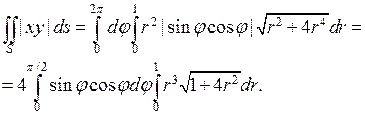
Таким образом, мы пришли к вычислению произведения двух интегралов по отрезкам.
2. Найти массу полусферы 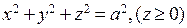 , плотность которой в каждой ее точке равна
, плотность которой в каждой ее точке равна  .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 416; Нарушение авторских прав?; Мы поможем в написании вашей работы!