Связь интеграла по замкнутой поверхности с тройным интегралом по телу, ограниченному этой поверхностью. Формула Гаусса-Остроградского

Пусть S – двусторонняя замкнутая поверхность, ограничивающая тело V. Предположим, что функции 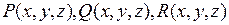имеют непрерывные частные производные в V и непрерывны на S. Докажем справедливость формулы Гаусса-Остроградского:

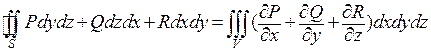, (ФГО)

где поверхностный интеграл взят по внешней стороне поверхности S.

Доказывать формулу Гаусса-Остроградского будем отдельно для каждого слагаемого в подынтегральном выражении.

Докажем, что .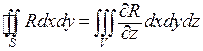

1. Сначала представим, что поверхность S либо пересекается любой прямой, параллельной оси OZ не более, чем в двух точках, либо отрезок этой прямой принадлежит S.

В этом случае поверхность S проецируется на область на плоскости XOY и можно параметризовать S следующим образом: 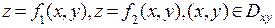, где 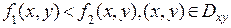. При этом та часть поверхности S, которая содержит отрезки прямых, параллельных оси OZ (обозначим ее 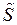), проецируется на граничные точки . Интеграл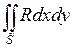по этой части поверхности равен нулю. Учитывая, что поверхностный интеграл взят по внешней стороне поверхности, получим 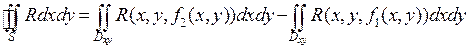, что дает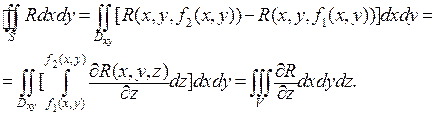

2. Для того, чтобы доказать формулу 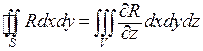в общем случае, разобьем тело V поверхностями, параллельными оси OZ, на конечное число тел 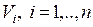, с граничными поверхностями 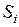, удовлетворяющими требованиям предыдущего пункта. Для каждого из полученных тел и соответствующих граничных поверхностей формула Гаусса-Остроградского справедлива. Поскольку интегралы по поверхностям, параллельным оси OZ и входящим в качестве слагаемых в интегралы по поверхностям 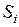, равны нулям, получим ,

что и требовалось доказать.

Соотношения 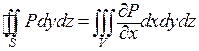и 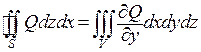доказываются аналогично. Таким образом, справедливость формулы Гаусса-Остроградского доказана.

Дата добавления: 2014-01-07