Алгоритм представления булевой функции полиномами Жегалкина

Приведённый выше алгоритм представления булевой функции полиномами Жегалкина является достаточно сложным и некомпактным, отнимающим большое время на осуществление данного представления булевой функции. При многочисленном построении КУ был найден более простой алгоритм представления булевой функции полиномами Жегалкина, позволяющий значительно снизить временные ресурсы на стадии проектирования. Суть данного метода состоит в последовательном применении двух простых действий:

1. Приводим заданную булеву функцию к совершенной конъюнктивной форме. Если булева функция задана в совершенной дизъюнктивной форме, то её следует привести к совершенной конъюнктивной форме путём использования правила Деморгана:

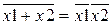
2. Заменяем все отрицания в совершенной конъюнктивной форме по формуле . Это справедливо, если обратиться к таблице:

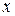
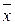
Пример. Представить полиномами Жегалкина булеву функцию:

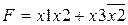
1. Приводим булеву функцию к совершенной конъюнктивной форме, используя правило Деморгана:

.

2. Заменяем все отрицания на :

Дата добавления: 2014-01-07