Зависимость проницаемости от пористости. Классификация проницаемых пород

Классификация проницаемых пород

По характеру проницаемости (классификация Теодоровича Г. И.) различают коллектора:

- равномерно проницаемые;

- неравномерно проницаемые;

- трещиноватые.

По величине проницаемости (мкм²) для нефти выделяют 5 классов коллекторов:

1. очень хорошо проницаемые (>1);

2. хорошо проницаемые (0,1 – 1);

3. средне проницаемые (0,01 – 0,1);

4. слабопроницаемые (0,001 – 0,01);

5. плохопроницаемые (<0,001).

Для классификации коллекторов газовых месторождений используют 1–4 классы коллекторов.

Теоретически, для хорошо отсортированного материала (песок мономиктовый) проницаемость не зависит от пористости.

Для реальных коллекторов в общем случае более пористые породы являются более проницаемыми.

Зависимость проницаемости от размера пор для фильтрации через капиллярные поры идеально пористой среды оценивается из соотношения уравнений Пуазейля и Дарси. В этом случае пористая среда представляется в виде системы прямых трубок одинакового сечения длиной L, равной длине пористой среды.

Уравнение Пуазейля описывает объёмную скорость течения жидкости через такую пористую среду:

, (1.22)

где r – радиус порового канала;

L – длина порового канала;

n – число пор, приходящихся на единицу площади фильтрации;

F – площадь фильтрации;

m – вязкость жидкости;

DР – перепад давлений.

Коэффициент пористости среды, через которую проходит фильтрация:

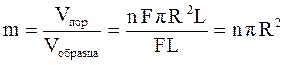. (1.23)

Следовательно, уравнение (1.22) можно переписать следующим образом:

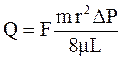. (1.24)

Из уравнения Дарси следует, что:

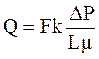. (1.25)

Приравняв правые части уравнений (1.24) и (1.25) получим взаимосвязь пористости и проницаемости:

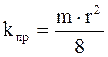. (1.26)

Из чего следует, что размер порового канала будет равен:

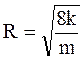. (1.27)

Если выразить проницаемость в мкм², то радиус поровых каналов (в мкм) будет равен:

. (1.28)

Оценка проницаемости для фильтрации через трещиноватые поры оценивается из соотношения уравнений Букингема и Дарси.

Потери давления при течении жидкости через щель очень малой высоты оцениваются уравнением Букингема:

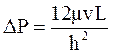, (1.29)

где h – высота трещины;

v – линейная скорость фильтрации.

Подставив это выражение в уравнение Дарси, получим:

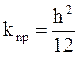. (1.30)

Соотношения (1.25) и (1.26) справедливы только для идеальной пористой среды (например, кварцевый песок).

Для реальных условий используется эмпирическое уравнение Котяхова:

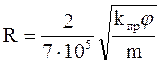, (1.31)

где R – радиус пор;

j – структурный коэффициент, описывающий извилистость порового пространства.

Значение j можно оценить путём измерения электросопротивления пород. Для керамических пористых сред при изменении пористости от 0,39 до 0,28, по экспериментальным данным, j изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно оценить по эмпирической формуле:

. (1.32)

Дата добавления: 2014-01-07