Ошибки полиномиальной интерполяции

End.

Begin

Begin

Begin

Var

Type

Const

Пример.

program PLagrang;

{вычисление полинома Лагранжа в n+1 узле интерполяции}

Uses Crt;

M=15;

RealType = Real;

Vec=Array[0..M] of RealType;

i, j, N: Integer;

p, L, x1: RealType;

x, y: Vec;

ch: Char;

ClrScr;

WriteLn ('Введите N - порядок многочлена Лагранжа');

Read (n);

WriteLn('Введите пары значений xi, yi; i= 0,...,N');

For i:= 0 to N do

Read (x[i],y[i]);

WriteLn;

end;

writeLn ('Введите x');

Read (x1);

L:= 0;

For i:= 0 to N do

p:= 1;

For j:= 0 to N do

If j<>i then p:= p*(x1-x[j])/(x[i]-x[j]);

L:= L + y[i]*p;

end;

WriteLn ('x = ', x1:8:4, ' L(x) = ',L:8:4);;

Repeat Until KeyPressed; {Ожидает нажатия любой клавиши, модуль Crt}

{Используется для задержки информации на экране}

ClrScr;{Очищает экран, модуль Crt}

Предположим, что величина 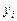представляет собой точные значения известной функции 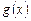в точках 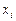. Пусть 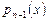- единственный полином 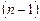-й степени, интерполирующий функцию по этим 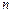точкам 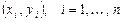. Предположим, что во всех 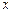функция имеет 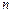непрерывных производных. Тогда можно доказать, что для любого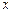

,

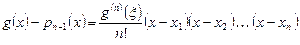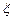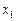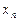где - некоторая неизвестная точка между и . Практическую пользу из этого выражения можно извлечь только в простых случаях, когда оно даёт границы ошибок.

Если интерполировать известную функцию 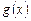в большем числе точек, то выражение для погрешности, состоящее из трёх разных частей, будет вести себя следующим образом:

· факториал и произведение разностей с увеличением 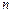уменьшают ошибку;

· порядок производной при этом растёт.

Для большинства функций величины производных увеличиваются быстрее, чем 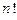. В результате полиномиальные интерполянты редко сходятся к обычной непрерывной функции.

Практический эффект выражается в том, что полиномиальный интерполянт высокой степени может вести себя очень плохо в точках 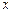, отличных от узловых 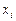. Поэтому используются интерполянты степени не выше 4 или 5.

Полиномиальная интерполяция высокой степени – плохая идея.

Дата добавления: 2014-01-07