Глоссарий

Астана

1. өлшемді евклидтік кеңістік – екі нүктенің ара қашықтығы 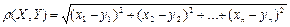формула бойынша анықталатын нүктелер жиыны.

2. 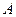нүктесінің 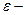маңайы - 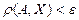теңсіздігін қанағаттандыратын 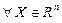нүктелер жиыны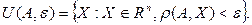

3. 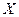нүктесі 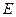жиынының ішкі нүктесі - 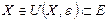кірістіруі, орындалатындай 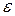оң саны табылады ()

4. Көп айнымалының функциясы -анықталу жиыны 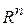-нің жиыншасы болатын функция.

5. 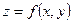функциясы 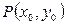нүктесінде үзіліссіз - .

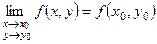6. Екі айнымал 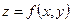функцияның өсімшелері – 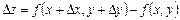толық өсімше, 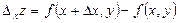- 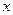аргументі бойынша дербес өсімше,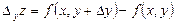 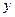аргументі бойынша дербес өсімше.

7. Екі айнымал 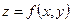функциясының 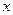айнымалы бойынша дербес туындысы .

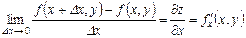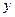айнымалы бойынша дербес туындысы .

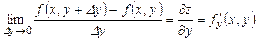8. 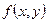функциясын 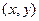нүктесінде дифференциалданады - егер 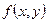функциясының 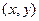нүктесіндегі толық өсімшесі

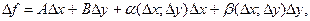(1)

түрінде өрнектелсе. Мұндағы, 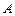, 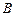коэффициенттері 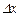, 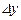өсімшелерінен тәуелсіз ал, α (Δ x; Δ y) және β (Δ x; Δ y) шексіз аз шамалар, егер Δ x →0, Δ y →0.

9. Толық дифференциал -(1) формуласымен анықталатын өсімшесінің сызықты бөлігі

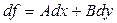
10. Сандық қатар - 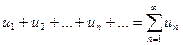ақырсыз қосынды.

11. Сандық қатардың дербес қосындылары –саны ақырлы мүшелерінің қосындысы:

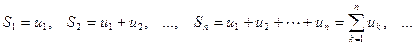
12. Жинақты қатар - егер 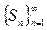сандық тізбегінің 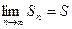нақты мәнді шегі бар болса.

13. Қатар жинақтылығының Даламбер белгісі -

а) 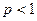болса, қатар жинақты; ә) 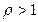болса, жинақсыз

14. Қатар жинақтылығының Коши белгісі -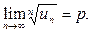

а) 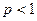болса, қатар жинақты; ә) 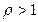болса, жинақсыз

15. Дәрежелік 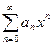қатарының жинақтылық радиусы – теріс емес 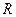нақты саны табылып, барлық 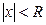нүктеде қатар жинақты, ал бар 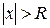нүктеде қатар жинақсыз.

16. Дифференциалдық теңдеу -ізделінетін функция бір немесм бірнеше айнымалыдан тәуелді және тәуелсіз айнымалылар бойынша алынған оның туындыларын байланыстыратын теңдеу

17. Жәй дифференциалдық теңдеу - дифференциалдық теңдеудегі ізделінетін функция тек қана бір айнымалыға тәуелді болса. .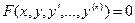

18. Дифференциалдық теңдеудің реті - теңдеудегі ізделінетін функция туындысының ең жоғарғы реті.

19. Дифференциалдық теңдеудің шешімі -дифференциалдық теңдеуді қанағаттандыратын кез келген функция.

Дәрістердің қысқаша мазмұны

1-дәріс. Функция. Сандар тізбегі

1. Жиындар. Логикалық символдар.

Белгілі бір ортақ қасиеттері бар элементтердің жиынтығын жиын деп атайды. Яғни, өзара бөлек заттар біріктіріліп, бір зат ретінде қарастырылады. Оның құрамындағы элементтердің (заттардың) әрқайсысын жиынның элементі деп атайды.

Жиынды үлкен әріптермен (А, В, С,...), ал оның элементтерін кіші әріптермен (а, b, с, ...) белгілеу қабылданған. Жиынды, көп жағдайда А ={ х } символымен белгілейді, мұндағы х жиын элементтерінің белгіленуі. Мысалы, А = { а, b, с,... }, .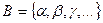

Егер А жиыны қандай да бір Р қасиетіне ие болатын элементтерден тұрса, онда ол 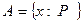арқылы жазылады. Мысалы, жазуы, 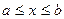теңсіздігін қанағаттандыратын х нақты сандар жиынын білдіреді. Бұл жиынды 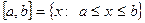түрінде жазуға да болады.

Бірдей элементтерден тұратын жиындарды тең жиындар деп атайды. Егер А және В жиындар тең болса, оны А = В арқылы белгілейді.

Егер В жиынының әрбір элементі А жиынының да элементі болса, онда В жиынын А жиынының жиыншасы деп атайды. Оны 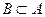символымен белгілейді. Әр уақытта 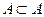болады.

Ешбір элементі жоқ жиынды бос жиын деп атап, 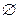символымен белгілейді. Бос жиын кез келген жиынның жиыншасы болып табылады. Сонымен, кез келген А жиынының әруақытта екі жиыншасы бар. Олар А және .

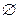Сандық жиындарды келесідей белгілейді:

N – барлық натурал сандар жиыны; Z - барлық бүтін сандар жиыны;

Q - барлық рационал сандар жиыны; R - барлық нақты сандар жиыны;

С - барлық комплекс сандар жиыны.

А және В жиындары берілсін. Егер А жиынының әрбір элементіне В жиынының белгілі бір элементі сәйкес қойылса, және керісінше, В жиынының әрбір элементіне А жиынының белгілі бір элементі сәйкес қойылса, онда А және В жиындарын эквивалентті деп атайды, оны А ~ В символымен белгілейді.

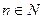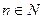Мысалы, барлық натурал сандар жиыны N және барлық жұп сандар жиыны М эквивалентті, яғни N ~ М. Шынында да, N және М жиындары арасында өзар бірмәнді сәйкестікті келесідей орнатуға болады: әрбір натурал санына саны, және керісінше әрбір санына натурал саны сәйкес қойылады.

Егер А ~ В және В ~ С болса, онда А ~ С екендігі айқын.

А жиынын ақырлы жиын деп атайды, егер n натурал саны табылып, А жиыны 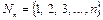жиынымен эквивалентті болса. Бұл жағдайда А жиынын n элементтті жиын деп те атайды.

Егер А жиыны ақырлы болмаса, онда оны ақырсыз не шектеусіз, шексіз жиын деп атайды. Яғни, әрбір n натурал саны үшін А жиынында бір-бірінен өзге болатын (n +1) элемент бар.

N – барлық натурал сандар жиыны, R - барлық нақты сандар жиыны ақырсыз жиын.

N – барлық натурал сандар жиынына эквивалентті жиынды саналатын деп атайды. Яғни, А жиыны саналатын жиын, егер ол ақырсыз және оның элементтерін нөмірлеп шығуға болатын боса.

Мысалы,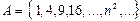, 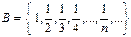саналатын жиындар.

А және В жиындарының қосындысы немесе бірігуі деп осы жиындардың кем дегенде біреуіне тиісті элементтерден тұратын жиынды атайды. Оны 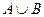арқылы белгілейді. Сонымен, егер қандай да бір элемент 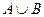жиынына тиісті болса, онда ол не тек қана А жиынына, не тек қана В жиынына, не осы екі жиынға да тиісті болады.

А және В жиындарының қиылысуы деп осы жиындардың екеуіне де тиісті элементтерден тұратын жиынды атайды. Оны 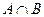арқылы белгілейді. Сонымен, егер қандай да бір элемент 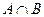жиынына тиісті болса, онда ол А жиынына да, В жиынына да тиісті болады.

А және В жиындарының айырымы деп А жинының В жиынына тиісті емес элементтерінен тұратын жиынды атайды. Оны 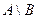арқылы белгілейді.

Егер 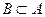болса, онда 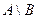айырымын В жиынының А жиынына дейінгі толықтаушысы деп атайды.

А және В жиындарының симметриялы айырымы деп 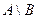және 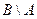жиындарының бірігуін атайды. Симметриялы айырымды 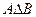символымен белгілейді.

Логикалық символдар. Кванторлар

Математикалық сөйлемдерде (анықтамаларда, теоремаларда, талдауларда) қандай да бір қасиетке ие «элемент табылады» және «кез келген элемент» үшін қандай да бір қасиет орындалады деген сияқты сөйлемшелер жиі кездеседі. Жиі кездесетін сөйлемшелерді квантор деп аталатын символдармен белгілеу ыңғайлы.

1) «кез келген», «барлық», «әрбір», «қандай да болмасын» сөйлемшелер математикада бір мағынада қолданылады да, 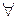(ағылшын тіліндегі Any- кез-келген сөзінің бірінші әрпінің төңкеріліп жазылуы) кванторымен;

2) «табылады», «белгілі бір» сөйлемшелер математикада бір мағынада қолданылады да, $ (ағылшын тіліндегі Existence- бар болу сөзінің бірінші әрпінің төңкеріліп жазылуы) кванторымен;

3) «шығады», «салдары» деген сөйлемшелер Þ кванторымен белгіленеді.

4) 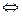символы, белгінің екі жағындағы тұжырымдардың тепе-теңдігін, яғни тең мағыналылығын білдірді;

5) def белгісі, айтылған тұжырымның анықтама бойынша дұрыстығын білдіреді.

Мысалы, «А жиынының әрбір х элементі үшін Р қасиеті орындалады» деген 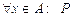түрінде, ал «В жиынынан Р қасиеті орындалатын 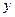элементі табылады» деген 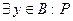түрінде жазылады.

Қарама-қарсы (кері) тұжырымдау ережесі.

Қарама-қарсы тұжырым құру үшін " және $ кванторлары қолданылып тұрған сөйлемшелерді өзгертпей, ал кванторларды өзара ауыстырып, (" орнына $, ал $ орнына " кванторын қою керек), ал қорытындысы болатын тұжырымды оған қарама-қарсы тұжырымға ауыстыру керек.

Мысалы, болса, онда оған қарама-қарсы анықтама 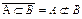кванторлар арқылы келесідей жазылады: 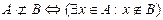. Яғни, В жиынында жатпайтын А - ның элементі бар.

Дата добавления: 2014-01-07