
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лейбниц формуласы
|
|
|
|
Егер 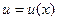 және
және  функцияларының
функцияларының 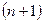 -ші ретке дейінгі туындылары бар болса, онда
-ші ретке дейінгі туындылары бар болса, онда
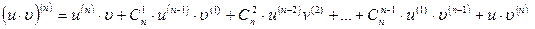 (4.14)
(4.14)
формуласы орынды болады. Мұнда 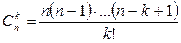 биномдық коэффициенттер. (14) формуланы Лейбниц формуласы деп атайды.
биномдық коэффициенттер. (14) формуланы Лейбниц формуласы деп атайды.
Егер көбейтіліп тұрған функциялардың біреуінің туындылары белгілі бір реттен бастап нөлге айналып, екіншісінің туындылары оңай табылса, онда Лейбниц формуласын қолдану нәтижелі болады.
Мысалы,  функциясының
функциясының 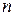 - ші ретті туындысын табайық.
- ші ретті туындысын табайық.
Шешуі. Егер 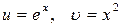 болса, онда
болса, онда 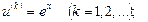
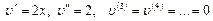 болады. Демек, (4.14) бойынша
болады. Демек, (4.14) бойынша
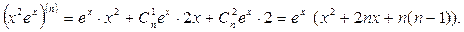
Параметр арқылы берілген функцияның жоғары ретті туындылары
Параметр арқылы берілген 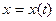 ,
, 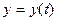 функцияны қарастырайық. Оның бірінші ретті туындысы
функцияны қарастырайық. Оның бірінші ретті туындысы  формуласымен анықталатындығы белгілі. Екінші ретті
формуласымен анықталатындығы белгілі. Екінші ретті 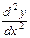 туындысын,
туындысын, 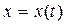 ,
, 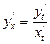 параметр арқылы берілген функцияның туындысы ретінде анықтау керек. Сонда, бірінші ретті туындыны анықтау формуласын және бөлшектің туындысын табу ережесін пайдалансақ, келесі формуланы аламыз:
параметр арқылы берілген функцияның туындысы ретінде анықтау керек. Сонда, бірінші ретті туындыны анықтау формуласын және бөлшектің туындысын табу ережесін пайдалансақ, келесі формуланы аламыз:
 .
.
Мысалы, 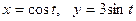 функциясының екінші ретті туындысын табайық.
функциясының екінші ретті туындысын табайық.
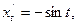
 болғандықтан
болғандықтан 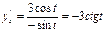 .
. 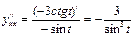 .
.
7. Дифференциалдық есептеудің негізгі теоремалары
Локальді экстремум. Егер 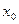 нүктесінің
нүктесінің 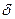 - маңайында функцияның қабылдаған мәндері сол нүктедегі мәнінен аспаса (кем болмаса), онда
- маңайында функцияның қабылдаған мәндері сол нүктедегі мәнінен аспаса (кем болмаса), онда 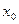 -ді сол функцияның локальді максимум (локальді минимум) нүктесі деп атайды. Сонымен
-ді сол функцияның локальді максимум (локальді минимум) нүктесі деп атайды. Сонымен 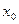 нүктесі
нүктесі  функциясының локальді максимум (локальді минимум) нүктесі болуы үшін
функциясының локальді максимум (локальді минимум) нүктесі болуы үшін  функциясы
функциясы 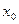 нүктесінің белгілі бір
нүктесінің белгілі бір 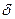 маңайында анықталып
маңайында анықталып
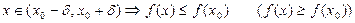 . (4.15)
. (4.15)
шарты орындалуы керек. Кейде (4.15) шарты
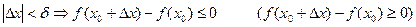 .
.
түрінде қолданылады.
Егер 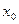 локальді максимум немесе локальді минимум нүктесі болса, онда оны локальді экстремум нүктесі деп атайды.
локальді максимум немесе локальді минимум нүктесі болса, онда оны локальді экстремум нүктесі деп атайды.
6-теорема (Ферма теоремасы). Егер  функциясы үшін х о локальді экстремум нүктесі болып, сол нүктеде
функциясы үшін х о локальді экстремум нүктесі болып, сол нүктеде  -тің ақырлы туындысы бар болса, онда сол туындының мәні нөлге тең болады.
-тің ақырлы туындысы бар болса, онда сол туындының мәні нөлге тең болады.
Ескертулер. 1. Экстремумның анықтамасындағы шарт  функциясының
функциясының 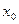 нүктесінің екі жақты маңайында орындалуы дифференциалдау теориясын пайдалану үшін қажет.
нүктесінің екі жақты маңайында орындалуы дифференциалдау теориясын пайдалану үшін қажет.
2. Кері тұжырым дұрыс емес, яғни 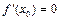 болса да,
болса да, 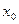 нүктесі экстремум нүктесі болмауы мүмкін.
нүктесі экстремум нүктесі болмауы мүмкін.
Мысалы, 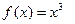 үшін
үшін 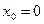 болғанда
болғанда 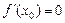 , бірақ
, бірақ 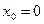 экстремум нүктесі емес
экстремум нүктесі емес
4.7-теорема (Ролль теоремасы).  функциясы
функциясы 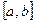 сегментінде анықталып, келесі шарттар орындалсын:
сегментінде анықталып, келесі шарттар орындалсын:
1) 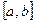 сегментінде үзіліссіз,
сегментінде үзіліссіз,
2)  интервалында дифференциалдансын,
интервалында дифференциалдансын,
3) 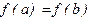 болсын.
болсын.
Онда  шартын қанағаттандыратын кемінде бір
шартын қанағаттандыратын кемінде бір  нүктесі табылады.
нүктесі табылады.
4.8-теорема (Лагранж теоремасы). Егер  функциясы
функциясы  сегментінде үзіліссіз болып,
сегментінде үзіліссіз болып, 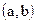 интервалында дифференциалданса, онда
интервалында дифференциалданса, онда
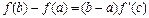 (4.16)
(4.16)
теңдігі орындалатын кемінде бір 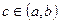 нүктесі табылады.
нүктесі табылады.
(4.16) - формуланы Лагранж формуласы немесе ақырлы өсімшелер формуласы деп те атайды.
4.9-теорема (Коши теоремасы). Егер  және
және 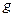 функциялары
функциялары 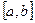 сегментінде үзіліссіз болып,
сегментінде үзіліссіз болып, 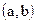 интервалында дифференциалданса, онда
интервалында дифференциалданса, онда
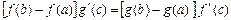 . (4.17)
. (4.17)
теңдігі орындалатын кемінде бір 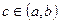 нүктесі бар болады.
нүктесі бар болады.
4-дәріс. Анықталмаған интеграл
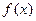 және
және 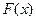 функциялары
функциялары 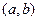 сан аралығында анықталған және үзіліссіз функция болсын.
сан аралығында анықталған және үзіліссіз функция болсын.
Анықтама. Егер 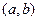 аралығында дифференциалданатын
аралығында дифференциалданатын 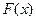 функциясы
функциясы
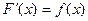 немесе
немесе 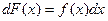 (1)
(1)
теңдіктерін барлық  үшін қанағаттандырса, онда осы аралықта үзіліссіз
үшін қанағаттандырса, онда осы аралықта үзіліссіз 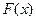 функциясы
функциясы 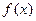 функциясының алғашқы функциясы деп аталады.
функциясының алғашқы функциясы деп аталады.
Мысалы, 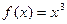 функциясының алғашқы функциясы
функциясының алғашқы функциясы 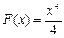 болады. Шынында да,
болады. Шынында да,  .
.
Бұл функцияның алғашқы функциясы бір мәнді болмайды, себебі 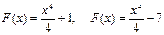 немесе жалпы
немесе жалпы 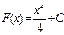 функциясы да С – ның кез келген мәнінде
функциясы да С – ның кез келген мәнінде 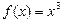 функциясының алғашқы функциясы болады, яғни
функциясының алғашқы функциясы болады, яғни  .
.
Қорыта айтқанда, егер берілген f (x) функциясының алғашқы функциясы F(x) болса, онда бұдан басқа алғашқы функциялардың түрі  болады.
болады.
Анықтама. 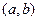 аралығындағы
аралығындағы  функциясының барлық алғашқы функцияларының жиыны осы функцияның анықталмаған интегралы деп аталады.
функциясының барлық алғашқы функцияларының жиыны осы функцияның анықталмаған интегралы деп аталады.
Оны 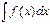 таңбасымен белгілейді.
таңбасымен белгілейді.
Алғашқы функциялардың бар болуы туралы негізгі теорема.
Теорема. Кез келген үзіліссіз функцияның шексіз көп алғашқы функциялары болады. Егер 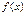 функциясының алғашқы функцияларының бірі
функциясының алғашқы функцияларының бірі 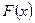 болса, кез келген басқасын
болса, кез келген басқасын 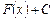 түрінде өрнектеуге болады:
түрінде өрнектеуге болады:
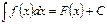 , (2)
, (2)
мұндағы 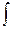 анықталмаған интеграл таңбасы,
анықталмаған интеграл таңбасы, 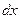 -
- 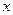 айнымалысының дифференциалы,
айнымалысының дифференциалы, 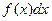 - интеграл астындағы өрнек, ал
- интеграл астындағы өрнек, ал 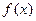 - интеграл астындығы функция,
- интеграл астындығы функция, 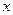 - интегралдау айнымалы; С –тұрақты.
- интегралдау айнымалы; С –тұрақты.
Берілген функцияның алғашқы функциясын табу интегралдау амалы деп аталады.
Теорема (анықталмаған интегралдың бар болу шарты). Егер 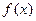 функциясы үзіліссіз болса, онда оның анықталмаған интегралы бар болады.
функциясы үзіліссіз болса, онда оның анықталмаған интегралы бар болады.
Мысалдар. 1.  , себебі
, себебі 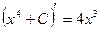 .
.
2. 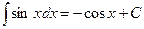 , себебі
, себебі 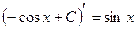 .
.
3. 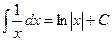 , себебі
, себебі 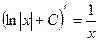 .
.
Анықталмаған интегралдың қасиеттері. Анықталмаған интегралдың анықтамасынан келесі қасиеттер шығады:
10. Анықталмаған интегралдан алынған туынды интеграл астындағы функцияға, ал анықталмаған интегралдан алынған дифференциал интеграл астындағы өрнекке тең:
 ,
, 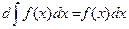 ;
;
20. Функция дифференциалынан алынған анықталмаған интеграл берілген функцияның өзі мен ерікті тұрақтының қосындысына тең:
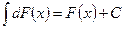 ;
;
30. Егер 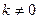 - тұрақты сан болса, онда тұрақты көбейткішті интеграл таңбасының алдына шығаруға болады:
- тұрақты сан болса, онда тұрақты көбейткішті интеграл таңбасының алдына шығаруға болады:
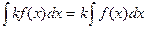 ;
;
40. Алгебралық қосындының анықталмаған интегралы жеке қосылғыштардан алынған интегралға тең:
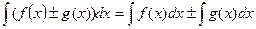 ;
;
50. Егер 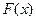 функциясы
функциясы 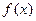 функциясы үшін алғашқы функция, яғни
функциясы үшін алғашқы функция, яғни 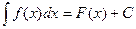 , болса, онда
, болса, онда
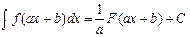 ,
,
мұндағы  және
және 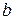 - тұрақты сандар.
- тұрақты сандар.
Анықталмаған интегралдардың негізгі кестесі.
1. 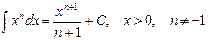 . 2.
. 2. 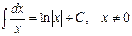 .
.
3.  . 4.
. 4.  .
.
5. 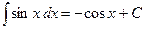 . 6.
. 6. 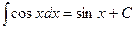 .
.
7. 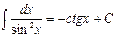 ,
, 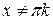 ,
, 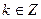 . 8.
. 8.  .
.
9. 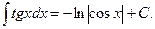 10.
10. 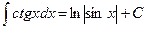 .
.
11. 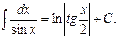 12.
12. 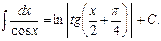
13. 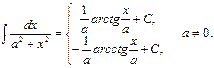
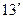 .
. 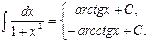
14.  =
=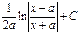 ,
, 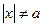 .
.
15. 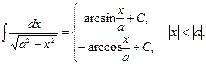
 .
. 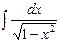
 =
=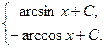
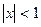 .
.
16. 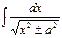 =
=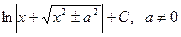 .
.
17. 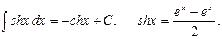 18.
18. 
19. 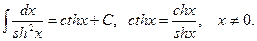 20.
20. 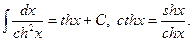
Мысалдар. 1. 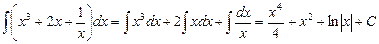 .
.
2. 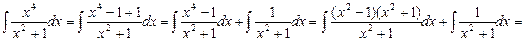
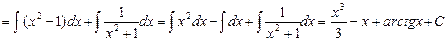 .
.
3.  .
.
1. Интегралдаудың негізгі әдістері
Интегралдаудың негізгі әдістері: тікелей интегралдау, айнымалыны алмастыру арқылы интегралдау, бөлiктеп интегралдау.
Тікелей интегралдау әдiсi
Интеграл астындағы функцияны түрлендіріп, анықталмаған интегралдың қасиеттері мен интегралдар кестесін қолданып интегралдауды тікелей интегралдау әдісі деп атайды.
Мысалдар. 1. 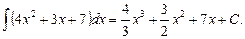
2. 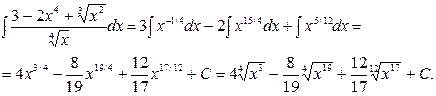
3. 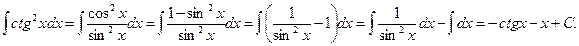
4. 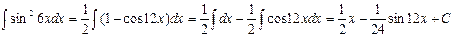 .
.
Айнымалыны ауыстыру әдісі
Интегралдағы х айнымалысының орнына жаңа t айнымалысын енгізіп, берілген 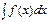 интегралын тікелей интегралданатын кестелік интегралдардың біріне келтіруге болады. Бұл интегралдау әдісін айнымалыны ауыстыру әдісі деп атайды. Бұл әдістің негізі күрделі функциялардың дифференциалдау формуласы болып табылады.
интегралын тікелей интегралданатын кестелік интегралдардың біріне келтіруге болады. Бұл интегралдау әдісін айнымалыны ауыстыру әдісі деп атайды. Бұл әдістің негізі күрделі функциялардың дифференциалдау формуласы болып табылады.
Теорема. Анықталмаған 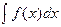 интегралындағы х айнымалысының орнына
интегралындағы х айнымалысының орнына 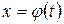 формуласы бойынша жаңа t айнымалысын енгізсек, берілген анықталмаған интеграл үшін
формуласы бойынша жаңа t айнымалысын енгізсек, берілген анықталмаған интеграл үшін
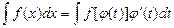 (3)
(3)
теңдігі орындалады.
Есеп шығарғанда интегралдың жауабын бастапқы айнымалы арқылы жазу керек.
Мысалдар. 1. 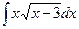
Шешуі. Квадрат түбірден құтылу үшін 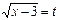 деп жаңа t айнымалы енгіземіз. Сонда
деп жаңа t айнымалы енгіземіз. Сонда 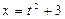 және
және 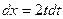 ауыстыруларын жасап, берілген интегралды кестелік интегралға келтіреміз:
ауыстыруларын жасап, берілген интегралды кестелік интегралға келтіреміз:

Интегралдың нәтижесін, 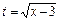 теңдігін ескеріп, бастапқы
теңдігін ескеріп, бастапқы  айнымалы арқылы жазамыз:
айнымалы арқылы жазамыз:
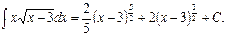
2. 
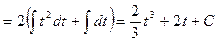 .
.
Интегралдың нәтижесін, 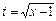 теңдігін ескеріп, бастапқы
теңдігін ескеріп, бастапқы  айнымалы арқылы жазамыз:
айнымалы арқылы жазамыз:
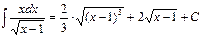 .
.
3. 
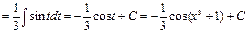 .
.
Салдар. Айталық, 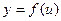 және
және  функциялары үзіліссіз болсын, онда
функциялары үзіліссіз болсын, онда
 . (5.4)
. (5.4)
Дифференциал таңбасы астында кез келген функцияның алғашқы функциясына тұрақтыны қосып немесе алып пайдаланғаннан дифференциалдың мәні өзгермейді, яғни 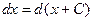 .
.
Дифференциал мен интегралдың қасиеттерін пайдаланып интегралдауды дифференциал таңбасы астына енгізу әдісі деп атайды.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2417; Нарушение авторских прав?; Мы поможем в написании вашей работы!