Мысалдар

Ньютон-Лейбниц формуласы

.

9⁰. Теорема (орташа мән туралы теорема). Егер 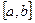аралығында х айнымалысы үшін 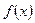функциясы үзіліссіз болса, онда

.

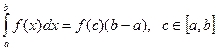10⁰. Анықталған интеграл үшін,

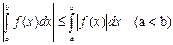
қатынасы орындалады.

Егер F (x) функциясы 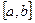аралығында интегралданатын 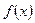функциясының алғашқы функциясы болса, онда

.

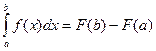1.. 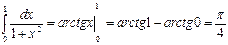. 2.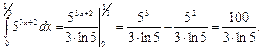

Анықталған интегралда айнымалыны ауыстыру.

Теорема. Егер 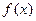функциясы 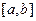кесіндісінде үзіліссіз, ал 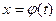функциясы 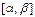кесіндісінде монотонды және үзіліссіз дифференциалданатын болса (мұндағы 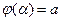, 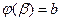), онда

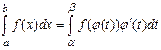
теңдігі орындалады. Бұл теңдік анықталған интегралда айнымалыны ауыстыру формуласы деп аталады.

Анықталған интегралды бөліктеп интегралдау.

Теорема. Егер u=u (x) және 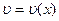функциялары 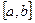кесіндісінде бірінші ретті туындыларымен бірге үзіліссіз болса, онда

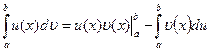
немесе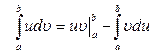

теңдігі орындалады. Бұл теңдік анықталған интегралды бөліктеп интегралдау формуласы деп аталады.

Мысалдар. Анықталған интегралдарды есептеңіз.

1.

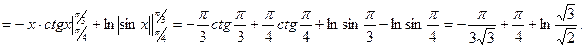
2.

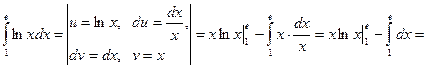
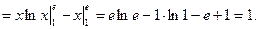
8. Анықталған интегралдың геометрияда қолданылуы

Тік бұрышты координаталардағы аудан

а) Егер 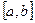кесіндісінде 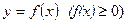болса, онда осы кесіндіде

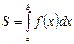
интегралы қисық сызықты трапецияның ауданын өрнектейді.

Ал, егер 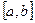кесіндісінде 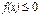болса, онда

.

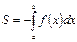б) Егер қисық сызықты трапециятөменнен және жоғарыдан сәйкес

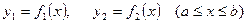функцияларының графиктерімен шектелген болса, онда ауданды мына формула бойынша есептейді:

.

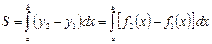в) 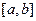кесіндісінде 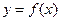функциясының графигі параметрлік функция түрінде берілсін: 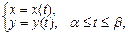мұнда 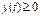үзіліссіз, ал 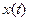функциясы 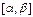кесіндісінде үзіліссіз дифференциалданатын функция, 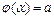, болса, онда ауданды мына формула бойынша есептейді:

.

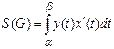г) Жазықтықта декарттық координаталар жүйесі берілсін. 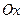оң жарты өсін полярлық өсі деп, ал нүктесін полюс деп атайды. 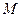нүктесі - жазықтықтағы кез келген нүкте болсын.

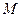нүктесінің декарттық және полярлық координаталарының арасындағы байланыс мына теңдіктің көмегімен анықталады:

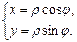
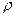және 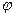сандарына мынадай шектеулер қолданылады:

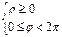(немесе ).

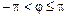Қисық сызықты сектордың ауданын мына формула бойынша есептейді:

.

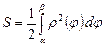Қисық доғасының ұзындығы

Егер 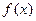функциясы өзінің туындысымен бірге 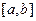кесіндісінде үзіліссіз болса, онда осы функция арқылы берілген АВ доғасының ұзындығын мына формула бойынша есептейді:

.

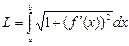б) Жазықтықта түзуленетін 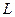қисығы параметрлік теңдеумен берілсін: 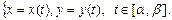Онда қисықтың ұзындығын мына формула бойынша есептейді:

.

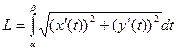в)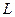 қисығы полярлық координаталар жүйесінде берілсін: .

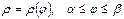Онда қисықтың ұзындығын мына формула бойынша есептейді:

.

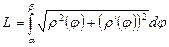7-дәріс. Көп айнымалының функциясы

Кеңістік пен жазықтықтағы жиындар.

Қарастырылатын екі айнымал функциялар 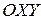декарттық координаталық жазықтығында, ал үш айнымалды функциялар үш өлшемді кеңістікте декарттық координаталар жүйесінде берілген деп есептейміз.

Мысалы, жазықтықта берілген нүктелер координаталары арқылы 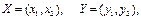ал кеңстіктегі нүктелер 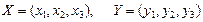түрінде жазылады.

Екі нүктенің ара қашықтығын 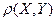арқылы белгілейміз. Екі нүктенің ара қашықтығы жазықтықта:

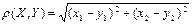
кеңістікте:

формулалары арқылы есептеледі.

Анықтама. 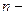өлшемді кеңістіктің 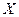нүктесі деп реттелген 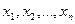нақты сандар жиынын атаймыз: 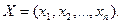Бұл жердегі 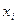сандары айнымалы 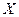нүктесінің 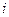- ші координаталары деп аталады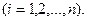

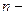өлшемді кеңістіктегі екі нүктенің ара-қашықтығы

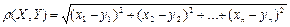(1)

формуласы арқылы есептеледі.

Анықтама. 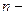өлшемді кеңістікте ара қашықтары (1) формула бойынша анықталатын нүктелер жиынын өлшемді евклидтік кеңістік немесе 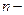өлшемді арифметикалық евклид кеңістігі деп атап, 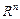арқылы белгіленеді.

Егер 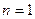болса, бір өлшемді кеңістік - түзу,

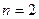болса, екі өлшемді кеңістік - жазықтық,

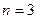болса, үш өлшемді кеңістік болатындығын элементар математикадан білеміз.

Анықтама. 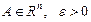болып, 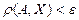теңсіздігін қанағаттандыратын 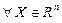жиыны - центрі 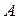нүктесі, радиусы 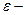ге тең шар немесе 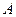нүктесінің 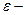маңайы деп аталады.

Сонымен,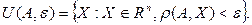

координаталық түрде жазсақ,

Егер 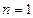болса, 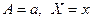болғандықтан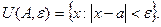

Егер 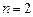болса,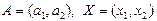

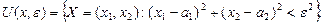
центрі – координатаның бас нүктесі, радиусы 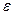болатын шеңбер.

Егер 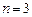болса,

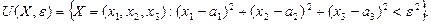
центрі 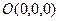– координатаның бас нүктесі, радиусы 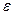болатын шар.

Көп айнымалы сандық функция

Мәндері қабылданатын жиын нақты сандар жиыны болатын функция сандық функция деп аталған еді. Анықталу жиыны жиыншасы болатын функция n айнымалылы функция деп аталады.

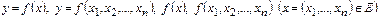
белгілеулері қолданылады.

Бірнеше тәуелсіз айнымалдардың 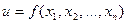немесе 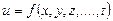функциясы осы әдіспен анықталады.

Функцияның анықталу жиыны

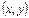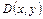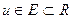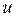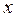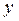Айталық, реттелген сандар жұбына облысында анықталған саны сәйкес келсін. Онда саны және айнымалдарының функциясы, 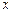, 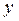– тәуелсіз айнымалдар немес аргументтер, – анықталу жиыны, ал функцияның барлық мәндерінің E жиыны оның мәндерінің жиыны деп аталады. Екі айнымал функцияның символдық жазылуы түрінде.

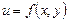функциясының анықталу жиыны қарапайым жағдайларда тұйық қисықпен шенелген жазықтықтың бөлігі ретінде беріледі. Анықталу жиынының шекарасы оған тиісті болуы да, болмауы да мүмкін.

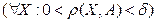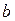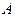Анықтама. Егер кез келген үшін қандай да бір саны табылып, үшін теңсіздігі орындалса, онда санын функциясының нүктесіндегі шегі деп атап, түрінде жазады.

Көп айнымал функцияның үзіліссіздігінің анықтамасы бір айнымал функцияның үзіліссіздігінің анықтамасы тәрізді функция шегімен тығыз байланысты.

Айталық, 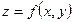функциясы 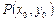нүктесінің маңайында анықталған болсын.

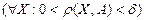Анықтама. Егер кез келген үшін қандай да бір саны табылып, үшін

теңсіздігі орындалса, онда 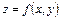функциясын 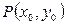нүктесінде үзіліссіз деп атайды.

Яғни,

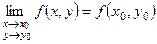(2)

теңдігі орындалатын болса.

, деп белгілесек, (2) теңдікті төмендегідей жазуға болады:

.

Дербес туындылар. Функцияның дифференциалы

Айталық, 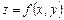функциясы нүктесінің қандай да бір маңайында анықталған болсын. нүктесінің 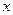айнымалысына қалауымызша алынған 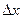өсімшесін беріп, ал y айнымалысын өзгеріссіз қалдырамыз, яғни жазықтықтың М (x; у) нүктесінен M₁ (x+ Δ x; у) нүктесіне көшеміз. Бұл жерде 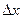-ті M₁ нүктесі М нүктесінің көрсетілген маңайында жататындай етіліп аламыз.

Анықтама. 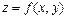функцияның 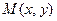нүктесіндегі x аргументі бойынша дербес өсімшесі деп айырмасын айтайды: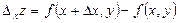

y аргументі бойынша дербес өсімшесі деп 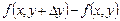айырмасын айтайды: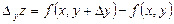

y және x аргументері бойынша толық өсімшесі деп 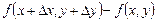айырмасын айтайды: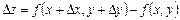

Анықтама. Қос айнымал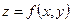функциясының x айнымалы бойынша алынған дербес туындысы деп,

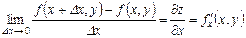
ақырлы шегін айтайды.

Ал y айнымалы бойынша алынған дербес туындысы деп,

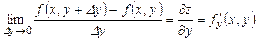
ақырлы шегін атайды.

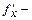табу кезінде турақты деп есептеледі, ал 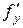тапқанда 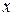- тұрақты деп есептеледі.

Анықтама. 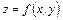функциясының дербес туындылары бар болса, онда оның дербес дифференциалдары деп

.

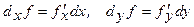өрнектерін атайды, мұндағы .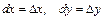

Екі айнымалы функцияның дербес дифференциалдары осы екі айнымалының біреуін тұрақты деп белгілеп алғандағы бір айнымалы функцияның дифференциалдары болып табылады.

Анықтама. Егер 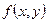функциясының 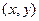нүктесіндегі толық өсімшесі

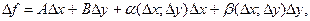(1)

түрінде өрнектелсе, онда 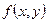функциясын 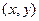нүктесінде дифференциалданады деп атайды. Мұндағы 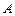, 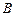коэффициенттері 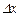, 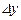өсімшелерінен тәуелсіз ал, α (Δ x; Δ y) және β (Δ x; Δ y) шексіз аз шамалар, егер Δ x →0, Δ y →0.

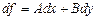
формуласымен анықталатын өсімшесінің сызықты бөлігін осы функцияның толық дифференциалы деп атайды.

Мұнда ,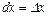

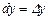
1-теорема. Егер 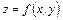функциясы 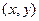нүктесінде дифференциалдатын болса, онда ол осы нүктеде үзіліссіз.

2-теорема. Егер 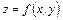функциясы 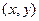нүктесінде дифференциалдатын болса, онда оның осы нүктед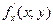е және дербес туындылары бар. Сонымен қатар 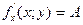, болады.

Онда функцияның толық дифференциалы келесідей өрнектеледі:

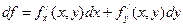(2)

Бірнеше айнымалы функцияның дифференциалдануы үшін дербес туындыларының бар болуы жеткіліксіз.

3-теорема. (Функция дифференциалдануының жеткілікті шарты). Егер 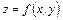функциясының 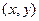нүктесінің қандай да бір δ маңайында дербес туындылары бар болып, олар 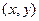нүктесінде үзіліссіз болса, онда функция 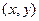нүктесінде дифференциалданады.

Күрделі функцияның туындысы

Анықтама. 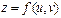, , 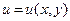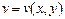функцияларынан құрылған күрделі функция деп екі 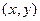айнымалыларынан тұратын 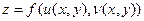функцияны айтамыз.

4-теорема. 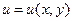, және 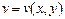функцияларының 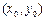нүктесінд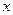е және 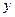бойынша дербес туындылары бар болсын, ал 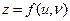функциясының 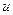мен 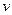бойынша дербес туындылары 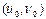нүктесінің маңайында үзіліссіз болсын, мұнда ,.

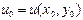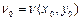Онда күрделі функцияның

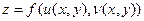(4)

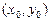нүктесінде дербес туындылары бар және мына формулалармен табылады:

(5)

Айталық 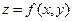екі айнымалының функциясы және 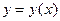бір айнымалының функциясы берілсін, сонда күрделі функциясының туындысын толық туынды деп атайды да былай белгілейді

.

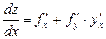Жоғары ретті туындылар

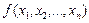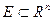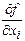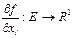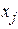
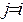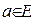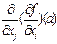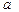сандық функциясы ашық жиынында анықталып, айнымалыларының бірі бойынша дербес туындысы бар болса, онда сол дербес туындының өзі түріндегі функция болып, белгілі бір болуы да мүмкін) айнымалысы бойынша нүктесінде дербес туындысы бар болуы мүмкін. Бұл санфункциясының нүктесінд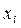е және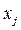айнымалылары бойынша алынған екінші ретті дербес туындысы деп аталады да, оны белгілеу үшін 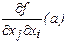, , 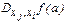, , 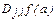, , 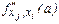, 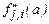т.б. символдар қолданылады. Мұнда i және 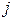индекстерінің жазылу реті дербес туынды әуелі бойынша, содан соң 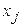бойынша алынғанын көрсетеді.

Дербес туынды алу амалын жалғастырып қолдана беруге болады: егер k -ретті 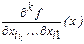дербес туындысы анықталған болса, онда -ші дербес туынды былай анықталады:.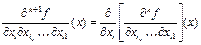

Сонымен, жоғары ретті дербес туындылар индуктивті әдіспен анықталады.

Аралас туындылар ұғымы көп айнымалылы функциялар жағдайында ғана мүмкүн. Келесі сұрақ өзінен-өзі айқын түрде туады: аралас туынды алу кезегі нәтижесіне әсер ете ме? Мәселен, әрқашанда 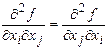теңдігі орындала бере ме?

Анықтама. 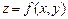функциясының 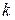ретті дербес туындысы деп оның 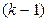ретті кезкелген туындысының дербес туындысын айтайды.

Бұл рекуренттік анықтама функцияның 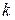ретті дербес туындысын бұл функцияның 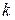дербес туындыларын бірінің артынан бірін табу жолымен табу мүмкіндігін береді. 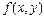функциясы нөлінші ретті туынды деп есептеледі.

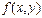ункциясының бірінші ретті 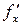және 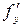туындыларынан 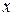,бойынша туындылар алып төрт екінші ретті туындылар аламыз:

.

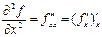
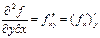
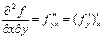
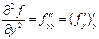Бұлардан 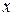,бойынша тағы да туындылар алып 3-і ретті 8 дербес туындыларды табамыз. 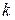ретті екі айнымалының 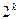туындысы бар.

Мысал. функциясының 2-ретті дербес туындыларын табайық.

, , ,

, , .

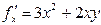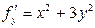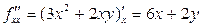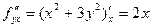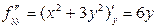Бұл мысалда 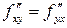және бұл кездейсоқ емес.

Екінші ретті дербес туындылар деп бірінші ретті дербес туындылардан алынған дербес туындыларды айтады:

.

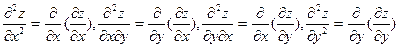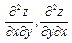дербес туындыларын аралас туындылар деп атайды.

7-теорема. Егер 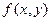функциясы 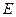ашық жиынында анықталып, әрбір 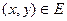нүктесінде 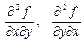дербес туындылары бар болсын. Егер осы екі функция 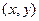нүктесінде үзіліссіз болса, онда сол нүктеде олардың мәндері өзара тең болады.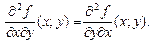

Салдар. 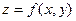функциясының 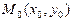нүктесінің маңайында 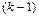–ге дейінгі барлық дербес туындылары, барлық 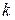ретті аралас туындылары үзіліссіз болсын. Онда бұл нүктеде оның 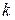ретті барлық аралас туындылары, тек дифференциалдау реті өзгеше, өз ара тең болады. Бұл салдар 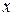бойынша 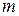, бойынша 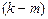дифференциалдары бар белгілеулер қолдануға болады:

.

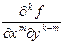Салдардың шарттары орындалғанда дифференциалдау реттері қортындыға әсер етпейді.

8-теорема. f және g сандық функциялары 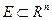ашық жиынында анықталып, 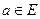нүктесінде дифференциалдаисын. Онда 1) кез келген 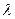және 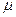, нақты сандары үшін 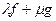сызықтық комбинациясы да а нүктесінде дифференциалданып, келесі теқдіктер орындалады:

1)

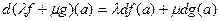
2) tg кебейтіндісі а нүктесінде дифференциалданып,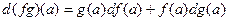

3) егер болса, оида 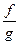бөліндісі а нүктесінде дифференциалданып,

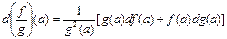
Анықтама. 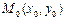нүктесінің маңайында 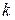ретке дейінгі барлық дербес туындылары бар және үзілісіз 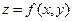функциясы осы нүктеде 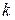рет дифференциаданатын функция деп аталады.

8- дәріс. Көп айнымалының функциясы

Айқындалмаған түрде берілген функцияны дифференциалдау

Егер бір айнымал функцияны қарастырсақ, у-пен аргумент х-тің арасындағы тәуелділікті әртүрлі әдістермен беруге болады. Егер у-ті айнымал х арқылы өрнектесек, яғни

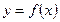(6)

түрінде жазсақ, онда функция айқындалған түрде берілген дейміз. Көптеген жағдайларда функцияны (1)-түрде өрнектей алмаймыз.

Егер у-пен аргумент х-тің арасындағы байланыс

(7)

теңдеуі түрінде берілсе және оның ең болмағанда бір шешімі бар болса, онда функция айқындалмаған түрде берілген деп аталады.

Мысалы, 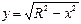функциясының графигі радиусы 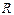- ге тең жоғарғы жарты шеңбер болып табылады. Осы функцияны мына айқын емес 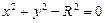, түрде жазуға болады. Ал, бұл функция сонымен қатар 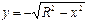функциясын анықтайды.

Ескерту. Кез келген айқындалған түрде берілген функцияны айқындалмаған түрде жазуға болады. Керісінше, айтылған тұжырым дұрыс болмайды. Мысалы,

функциялық теңдеуінде 1-ді теңдеудің сол жағына көшірсек,

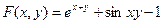
функциясы 1–ші теореманың шарттарын қанағаттандырады, яғни 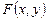функциясы және оның дербес туындылары айнымалдардың кез келген мәндерінде үзіліссіз болады. 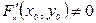болғандықтан, берілген теңдеуі бір мәнді айқындалмаған функцияны анықтайды.

Берілген функцияны айқындалған түрде жаза алмаймыз.

5-теорема 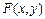функциясы

1) 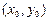нүктесінің маңайында үзіліссіз және 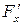, 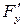үзіліссіз дербес туындылары бар,

2) ,

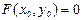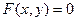3) болса, онда теңдеуі 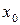нүктесінің маңайында дифференциалданатын 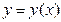функциясын анықтайды және

(8)

6-теорема. 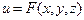функциясы

1) 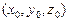нүктесінің маңайында үзіліссіз және оның 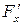, , 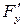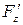үзіліссіз дербес туындылары бар болсын,

2) ,

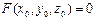3) 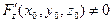болса, онда

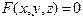теңдеуі 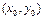нүктесінің маңайында дифференциалданатын 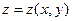функциясын анықтайды және оның дербес туындылары келесідей анықталады:

Екі айнымалы функцияның экстремумы

Айталық, 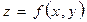қос анымалы функциясы G облысында берілсін, ол 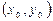- осы облыстың ішкі нүктесі болсын.

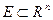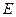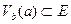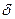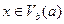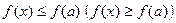Анықтама. сандық функциясы жиынында анықталсын. Егер, біріншіден, нүктесі жиынының ішкі нүктесі болса, екіншіден, кірістіруі орындалатындай қайсыбір оң саны мен әрбір үшін теңсіздігі орындалса, онда нүктесін 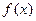функциясы локальді максимум (локальді минимум)мәнін қабылдайтын нүкте, не қысқаша - локальді максимум (локальді минимум) нүктесі деп атайды.

Егер 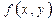функциясы үшін 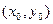нүктесінің маңайының барлық нүктесінде

_,

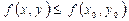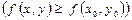
теңсіздігі орындалатын болса, онда 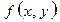функциясы 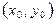нүктесінде максимумға (минимумға) ие болады деп атаймыз.

Максимум және минимум ұғымдары нүктелік (локальдық) ұғымдар.

Локальді максимум мен локальді минимум локальді экстремум деп аталады.

8-теорема (экстремумның қажетті шарты)

функциясы үшін эксремум нүктесі болсын.

Егер, сонымен қатар, 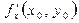және 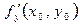бар және ақырлы болса, онда

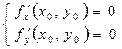
Салдар. Көп айнымал функциялардыңэкстремумдары әр аргумент бойынша алынған дербес туындылары бір кезде нөлге айналатын нүктелерде «(ғана емес, сонымен қатар,

1) бірінші ретті дербес туындыларының ең кемінде біреуі ақырсыздыққа айналатын нүктелерде

2) бірінші ретті дербес туындыларының ең кемінде біреуі анықталмаған нүктелерде болуы мүмкін.

Егер 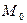нүктесінде 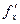, нольге тең болса, не анықталмаса, онда 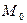нүктесі 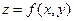функциясының күдікті (кризистік) нүктесі деп аталады.

Кез-келген кризистік нүктенің экстремум нүктесі болуы шарт емес.

Экстремумның бар болуының жеткілікті шарттары

9-теорема. Екі айнымалылы сандық 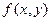функциясы 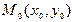нүктесінің қайсыбір 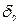–маңайында анықталып, сол маңайда

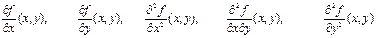
дербес туындылары бар және үзіліссіз болып, сол нүктенің өзінде локальді экстремумның қажетті шарты орындалсын: . Мынадай белгілеулер енгізейік:

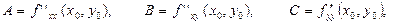
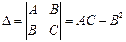
Онда:

1) егер 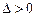болса, онда 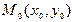локальді экстремум нүктесі болып, 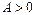болғанда локальді қатаң минимум, 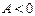болған да локальді қатаң максимум нүктесі болады;

2) егер 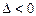болса, онда 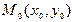нүктесі локальді экстремум нүктесі емес;

3) егер 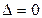болса, онда 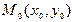нүктесі туралы нақтылы ештеңе айтуға болмайды: ол локальді экстремум нүктесі болуы да, болмауы да мүмкін.

9 - дәріс. Дифференциалдық теңдеулер

Анықтама. Тәуелсіз х айнымалы, ізделінетін функция және тәуелсіз айнымалы бойынша алынған оның туындыларын байланыстыратын

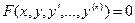(1)

теңдігі дифференциалдық теңдеу деп аталады.

Теңдеуге кіретін туындылардың ең жоғарғы реті теңдеудің реті деп аталады.

Егер (9.1) дифференциалдық теңдеуді ең жоғарғы туындысы арқылы шешіп,

(2)

түрінде жазсақ, ол қалыпты түрдегі дифференциалдық теңдеу деп аталады.

Егер дифференциалдық теңдеудегі ізделінетін функция тек қана бір айнымалыға тәуелді болса, онда ол жәй дифференциалдық теңдеу, ал бірнеше айнымалылардан тәуелді болса, онда дербес туындылы дифференциалдық теңдеу деп аталады.

Дифференциялдық теңдеуді қанағаттандыратын кез-келген функция осы теңдеудің шешімі немесе интегралы деп аталады.

Ерікті тұрақтылардың саны теңдеудің ретіне тең болатын дифференциялдық теңдеудің шешімі (егер ол бар болса) берілген дифференциялдық теңдеудің жалпы шешімі деп аталады.

Мысалы, 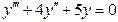- үшінші ретті жәй дифференциалдық теңдеу, - бірінші ретті, 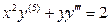- бесінші ретті; ал 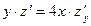- бірінші ретті дербес туындылы дифференциалдық теңдеу болып табылады.

Дербес шешім бір айнымалы функция болғандықтан, оның графигі дифференциялдық теңдеудің интегралдық қисығы деп аталады. Жалпы шешімге барлық интегралдық қисықтардың жалпы жиыны сәйкес келеді. Ол жалпы дифференциялдық теңдеудің интегралдық қисықтар жиынтығы деп аталады. Ал дифференциалдық теңдеудің шешімін анықтау жолы, осы теңдеуді интегралдау деп аталады.

Бірінші ретті дифференциалдық теңдеулер

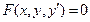(3)

түріндегі теңдеу бірінші ретті дифференциалдық теңдеу деп аталады.

(4)

түріндегі теңдеу бірінші ретті туындысы бойынша анықталған қалыпты түрдегі дифференциалдық теңдеу деп аталады.

Бірінші ретті туындысы бойынша анықталған қалыпты түрдегідифференциалдық теңдеудің дифференциалдық түрде жазылуы:

,

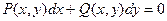мұндағы 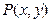және 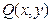анықталған берілген функциялар.

Дифференциалдық теңдеулерге мысалдар келтірейік:

, , , .

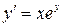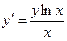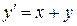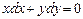Анықтама. Бірінші ретті жәй дифференциалдық теңдеудің шешімі деп,

1) 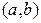аралығында үзіліссіз диффренциалданатын 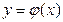функциясы түрінде;

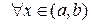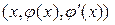2) үшін нүктесі F функциясының анықталу аймағы болатын 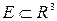жиынында жататын;

3) үшін 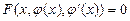тепе-теңдігі орындалатын, 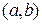аралығында анықталған функцияны айтады.

Көбінесе «шешім деп, (4) теңдеуді қанағаттандыратын, яғни тепе-теңдікке айналдыратын функцияны айтамыз» дей береді.

Ал, шешімдерінің ішінен тек біреуін таңдап алу үшін қосымша шарттар қою арқылы, Коши есебін шешеміз: 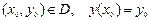- бастапқы шарт немесе Коши шарты. (9.4) дифференциалдық теңдеудің бастапқы шартты қанағаттандыратын шешімі дербес шешім, ал есеп – Коши есебі деп аталады.

(4) бірінші ретті дифференциалдық теңдеудің жалпы шешімі деп,

1) кез келген С демеуші мәндері үшін функциясы (4) теңдеудің шешімі болып табылатын;

2) кез келген 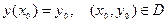бастапқы шарт үшін, С ₀ демеуші тауып, 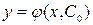функциясы 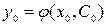шартын қанағаттандыратындай С демеушісінен тәуелді біріне-бірі ұқсас функциялар жиынтығын айтады.

Ал, бұл теңдеулердің дербес шешімі деп, С демеушісінің белгілі бір мәніне сәйкес жалпы шешімнен бөлініп алынған шешімді айтамыз. Ендеше, дербес шешім Коши есебінің шешімі болып табылады.

Теорема (Коши есебі шешімінің бар және оның жалғыздығы жөнінде). Егер 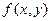функциясы D облысында анықталған, үзіліссіз және оның дербес туындысы 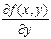болса, онда 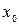нүктесінің 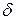- маңайы, яғни 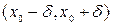табылып, осы маңайда (4) дифференциалдық теңдеудің бастапқы шартты қанағаттандыратын шешімі бар және ол жалғыз болады.

(4) бірінші ретті дифференциалдық теңдеудің әрбір нүктесіндегі шешімнің жалғыздығы бұзылатын, яғни 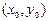нүктесі арқылы басқа да (4) теңдеуінің шешімдері басып өтетін болса, онда ол ерекше шешім деп аталады.

Бірінші ретті дифференциалдық теңдеулерді шешу.

а) Айнымалылары ажыратылған дифференциалдық теңдеулер. 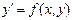дифференциалдық теңдеудің оң жағындағы 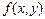функциясы біреуі у – тен тәуелсіз, екіншісі х –тен тәуелсіз екі функцияның көбейтіндісінен, яғни 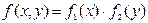тұрса, онда

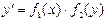(5)

теңдеу айнымалылары ажыратылған дифференциалдық теңдеу деп аталады. Айнымалылары ажыратылған дифференциалдық теңдеу мына түрде жазылады:

.

Бір жағында х, екіншісінде у болатындай теңдеуді екі бөлікке бөлеміз: 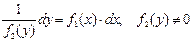. Сонда теңдеудің екі бөлігі екі функцияның дифференциалын береді, ендеше екі жағын жеке интегралдаймыз:

.

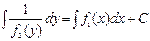Бұл бірінші ретті дифференциалдық теңдеудің жалпы шешімі (интегралы).

б) Айнымалылары ажыратылатын дифференциалдық теңдеулер.

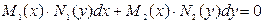. (6)

теңдеу айнымалылары ажыратылатын дифференциалдық теңдеу деп аталады. Онда 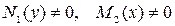деп болжап, осы теңдеуді 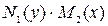- ке бөліп, айнымалылары ажыратылған дифференциалдық теңдеу аламыз:

.

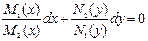Теңдеудің екі жағын да интегралдасақ,

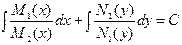
берілген дифференциалдық теңдеудің жалпы шешімін аламыз.

в) Біртекті дифференциалдық теңдеулер.

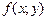функциясы берілсін. Егер кез келген 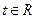нақты саны үшін

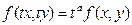
теңдігі орындалатын болса, онда 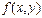функциясы 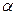- шы ретті біртекті функция деп аталады.

Егер 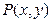және функциялары бірдей ретті біртекті функциялар болса, онда

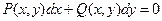(7)

біртекті дифференциалдық теңдеу деп аталады.

Анықтама. 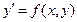түріндегі теңдеудің оң жағындағы 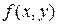функциясы нөлдік ретті біртекті функция бол

Дата добавления: 2014-01-07