
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системи лінійних алгебраїчних рівнянь
|
|
|
|
Вправи
Лінійна залежність і лінійна незалежність
Додавання рядків однієї довжини це додавання відповідних елементів. Множення рядка на число це множення всіх елементів рядка на це число.
Означення 1. Рядки (однієї довжини) називаються лінійно залежними, якщо один з них можна виразити через інші з допомогою додавання і множення на число. Аналогічно лінійно залежними можуть бути стовпчики, вектори, функції, рівняння.
Рядки називаються лінійно незалежними, якщо жоден з них не виражається через інші.
Зауваження. Якщо серед рядків є нульовий рядок, то очевидно, що він виражається через інші (взяти нульові коефіцієнти), тобто така сукупність є лінійно залежною. Тому один нульовий рядок теж називають лінійно залежним.
Означення 2. Рядки p1, p2,…, pn називаються лінійно залежними, якщо існують числа 𝜆1, 𝜆2,…, 𝜆n, не всі рівні нулю, що виконується рівність:
𝜆1×p1 +𝜆2×p2+…+𝜆n×pn = 0. (0 – нульовий рядок)
Ліва частина цієї рівності називається лінійною комбінацією рядків з коефіцієнтами 𝜆1, 𝜆2,…, 𝜆n.
Якщо лінійна комбінація рядків дорівнює нульовому рядку тільки при всіх нульових коефіцієнтах, то рядки називаються лінійно незалежними.
Теорема. Означення 1 і означення 2 еквівалентні.
Доведення. Нехай p1, p2,…, pn лінійно залежні рядки за означенням 1, тобто
наприклад, pn лінійно виражається через інші pn = с1×p1+с2× p2+…+сn-1×pn-1 .
Перенесемо всі доданки в праву частину: с1×p1+с2× p2+…+сn-1×pn-1 - pn =0.
Коефіцієнт біля pn дорівнює -1 (¹0). Тому також є лінійна залежність за означ.2.
Навпаки, якщо p1, p2,…, pn лінійно залежні за означенням 2:
𝜆1×p1 +𝜆2×p2+…+𝜆n×pn = 0, і наприклад 𝜆n¹0. То можна виразити рядок рn через інші:
рn = (-𝜆1 / 𝜆n)×p1 +(-𝜆2 / 𝜆n)×p2+…+(-𝜆n-1 / 𝜆n)×pn-1, тобто рядки лінійно залежні за означ.1.
1. Якщо серед рядків є нульовий, то вони лінійно залежні.
2. Якщо серед рядків є однакові рядки, або пропорційні, то вони також лінійно залежні.
3. Якщо до лінійно залежних рядків добавити деяку кількість рядків, то нова сукупність рядків залишиться лінійно залежною.
Властивість визначників 11. Визначник дорівнює нулю тоді і тільки тоді, коли його рядки (стовпці) лінійно залежні.
Доведення. Достатність. Нехай рядки p1, p2,…, pn визначника лін. залежні, тобто
𝜆1×p1 +𝜆2×p2+…+𝜆n×pn = 0, і наприклад 𝜆n¹0. Поділимо рівність на 𝜆n:
(𝜆1 / 𝜆n)×p1 +(𝜆2 / 𝜆n)×p2+…+(𝜆n-1 / 𝜆n)×pn-1, +рn = 0. Отже, якщо ми до рядка рn додамо попередні, помножені на числа (𝜆і / 𝜆n), то визначник не зміниться, але на місці рядка рn отримаємо нульовий рядок, тобто визначник дорівнює нулю.
Необхідність. Нехай визначник D =0. Якщо в нього є нульовий рядок, то рядки вже лінійно залежні. Припустимо, що немає нульового рядка. Отже, в першому рядку є ненульовий елемент а1і. З допомогою додавання помноженого його на числа до інших рядків в і-тому стовпці під а1і можна зробити всі нулі. При цьому будь-який (не перший) рядок стане лінійною комбінацією його самого з коефіцієнтом 1 і першого рядка. Якщо після цієї операції появиться нульовий рядок, то це означає, що початкові рядки теж були лінійно залежними. Знайдемо в другому рядку ненульовий елемент а2j в деякому j-тому стовпці (j¹i) і, додаючи помножений другий рядок до інших рядків, зробимо всі нулі в даному j-тому стовпці, крім а2j. (При цьому і-тий стовпець не зміниться.) Якщо ще не буде нульового рядка, то повторюючи цю операцію n разів, ми прийдемо до визначника, в якому в кожному рядку і стовпці буде по одному ненульовому елементу, тобто цей визначник дорівнює добутку цих ненульових елементів із деяким знаком. Тому D ¹0. Протиріччя. Отже, на деякому кроці ми все ж таки отримаємо нульовий рядок, що й означатиме, що рядки лінійно залежні.
Системою лінійних алгебраїчних рівнянь називається система вигляду:
 a11x1+a12x2+…+a1nxn=b1 xi - невідомі
a11x1+a12x2+…+a1nxn=b1 xi - невідомі
a21x1+a22x2+…+a2nxn=b2 aij – коефіцієнти – відомі числа
… bi – вільні члени – відомі числа
am1x1+am2x2+…+amnxn=bm
Невідомі можна позначати x, y, z,... Алгебраїчна, бо зустрічаються тільки дії додавання і множення, Лінійна, бо невідомі входять не більш як в першому степені.
Розмір системи (m x n), де m – кількість рівнянь, n – кількість невідомих.
 Пр. 2x+y=-1 Система лінійних алгебраїчних рівнянь (2х2).
Пр. 2x+y=-1 Система лінійних алгебраїчних рівнянь (2х2).
x – 2y=7
Система називається однорідною, якщо всі вільні члени дорівнюють нулю.
Якщо хоча б один вільний член не нуль, то система неоднорідна.
Розв’язок системи – це сукупність значень невідомих, при підстановці яких в систему отримаємо всі правильні рівності.
Несумісна система - це система, яка не має розв’язків. (Відповідь. Ø)
Однорідна система не може бути несумісною, бо завжди має нульовий розв’язок (0; 0;...;0).
Еквівалентні системи – це системи, в яких однакові розв’язки.
Теорема. Система лінійних алгебраїчних рівнянь може мати один розв’язок, жодного розв’язку або безліч розв’язків.
Доведення. Якщо є два різні розв’язки (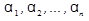 ) і (
) і (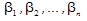 ), то можна побудувати ще один новий розв’язок – їх середнє арифметичне
), то можна побудувати ще один новий розв’язок – їх середнє арифметичне
( ), і аналогічно потім ще і ще.
), і аналогічно потім ще і ще.
Вам відомі такі методи розв’язування систем: виключення змінних шляхом підстановки або додавання рівнянь та для систем (2х2) графічний метод. Розглянемо метод розв’язування систем з допомогою визначників – метод Крамера.
Якщо в системі кількість рівнянь дорівнює кількості невідомих, то система називається квадратною.
Теорема Крамера. Якщо головний визначник квадратної системи не дорівнює нулю, тоді система має єдиний розв’язок, який можна знайти за формулами Крамера:
 х1=
х1=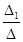 ; х2=
; х2= ; …;хn=
; …;хn= , де
, де
 - це допоміжні визначники, отримані з головного визначника заміною відповідного стовпчика на вільні члени:
- це допоміжні визначники, отримані з головного визначника заміною відповідного стовпчика на вільні члени:
 ,
, і т.д.
і т.д.
Доведення. Домножимо рівняння системи на відповідні алгебраїчні доповнення до елементів першого стовпця і додамо.
 A11 · a11x1+a12x2=b1
A11 · a11x1+a12x2=b1
A21 · a21x1+a22x2=b2 
x1(a11A11+a21A21)=x1Δ; x2(a12A11+a22A21)=0;
x1(a11A11+a21A21)+ x2(a12A11+a22A21)=b1A11+b2A21; b1A11+b2A21=Δ1, за властивістю Лапласа для першого стовпця
x1Δ=Δ1; Δ 0; х1=
0; х1=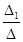 ; аналогічно для х2,…,хn
; аналогічно для х2,…,хn
Отже, розв’язок може бути тільки один. Ще треба перевірити чи ця пара чисел справді є розв’язком. Підставимо її в перше рівняння початкової системи: a11Δ1/Δ+ a12Δ2/Δ=b1 | · Δ a11Δ1+ a12Δ2=b1 Δ
a11(b1A11 +b2A21)+ a12(b1A12 +b2A22)= b1 (a11A11+a12A12)
 Підкреслені вирази в лівій і правій частині співпадають після розкривання дужок, а те що залишається в лівій частині: b2 (a11A21+a12A22)=0 за останньою властивістю визначників.
Підкреслені вирази в лівій і правій частині співпадають після розкривання дужок, а те що залишається в лівій частині: b2 (a11A21+a12A22)=0 за останньою властивістю визначників.
Пр. 2x+y=-1 Квадратна система лінійних алгебраїчних рівнянь (2х2).
x – 2y=7
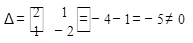 -- можна використати метод Крамера.
-- можна використати метод Крамера.
 ,
,
х=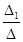 =-5/(-5)=1; y=
=-5/(-5)=1; y= =15/(-5)=-3; Перевірка: 2·1+(-3)=-1, 1-2·(-3)=7 вірно.
=15/(-5)=-3; Перевірка: 2·1+(-3)=-1, 1-2·(-3)=7 вірно.
Відповідь. {(1;-3)}.
Теорема про несумісну систему. Якщо в квадратній системі головний визначник дорівнює нулю, а хоча б один з допоміжних визначників Δі не дорівнює нулю, то система несумісна.
Доведення. Аналогічно як в доведенні теореми Крамера, отримаємо рівняння
xіΔ=Δі, яке очевидно не має розв’язків.
 Пр. 3х-4y+5z=-2 Квадратна система лінійних алгебраїчних рівнянь (3х3).
Пр. 3х-4y+5z=-2 Квадратна система лінійних алгебраїчних рівнянь (3х3).
2x+3y-z=1 Можна дослідити з допомогою визначників.
x-7y+6z=1
|

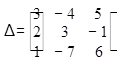 =
= (однакові рядки).
(однакові рядки).
Не можна використати метод Крамера.


|
 =
= =
=
=1(-1)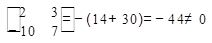 -- система не має розв’язків.
-- система не має розв’язків.
Відповідь. Ø.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1075; Нарушение авторских прав?; Мы поможем в написании вашей работы!