Взаємозв'язки індексів

Розглянуті зведені індекси узагальнюють динаміку складних
сукупностей. Не менш важливою в статистичному аналізі є друга функція індексів — аналітична, яка спирається на взаємозв’язок індексів. Практично кожний індекс є складовою певної індексної системи, а його зв’язки з іншими індексами цієї системи відбивають зв’язки між відповідними показниками. Так, товароборот залежить від фізичного обсягу проданого товару 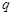і цін , відповідно індекс товарообороту 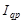можна подати як добуток індексів фізичного обсягу і цін:

Аналогічно грошові витрати на виробництво можна подати як функцію фізичного обсягу виробництва 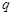і собівартості 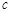, отже, обсяг виробництва — як функцію трудових затрат q та продуктивності праці , тобто і т. ін.

Отже, у будь-якій системі індекс добутку спряжених величин дорівнює добутку індексів цих величин. У рамках такої індексної системи на основі двох індексів можна визначити третій. Наприклад, якщо грошові витрати на виробництво зросли на 7,1%, а фізичний обсяг виробленої продукції — на 5%, то собівартість одиниці продукції зросла в середньому на 2%:

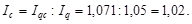
Взаємопов’язані також індекси прямих і обернених показників, наприклад, споживчих цін і купівельної спроможності грошової одиниці, продуктивності праці й трудомісткості продукції тощо. Якщо споживчі ціни зросли на 4,8%, то купівельна спроможність грошової одиниці зменшилася на 4,6%:

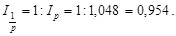
Показники-співмножники індексної системи є факторами показника-результату, а динаміка їх визначає динаміку останнього. Отже, у межах індексної системи можна визначити роль кожного окремого фактора, оцінити його вплив на динаміку результату. Така оцінка ґрунтується на методі абстракції. Аби виявити вплив одного фактора, необхідно абстрагуватись від впливу іншого, зафіксувати його на постійному рівні. Проте постає питання: на
рівні якого періоду — базисного чи поточного? Теоретично можливі два варіанти.

Перший: коли обидва індекси-співмножники базисно-зважені, кожний з них оцінює окремий вплив, оцінки впливу порівнянні. Проте цей варіант не забезпечує пов’язування індексів у систему:

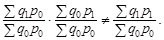
У другому варіанті індекси-співмножники різнозважені: ваги одного з них фіксуються на рівні базисного періоду, іншого — на рівні поточного. Через різнозваженість індексів оцінки впливу факторів непорівнянні, але саме такий порядок абстрагування впливу факторів забезпечує взаємозв’язок індексної системи:

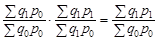
або

У розглянутому прикладі (див. табл. 9.2) результативний показник індексної системи — біржовий оборот. Його індекс обчислюється як відношення фактичних вартостей поточного періоду 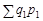= 27415 і базисного 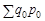= 23550:

,

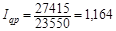тобто біржовий оборот зріс на 16,4%. Цей індекс можна записати як добуток індексів фізичного обсягу продажу і цін

1,164 = 1,181 × 0,986.

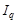Отже, зведені індекси цін і товарної маси , маючи самостійне значення, водночас виконують аналітичну функцію — оцінюють вплив відповідного фактора на динаміку біржового обороту. Ступінь впливу факторів на результат характеризують темпи приросту факторів. У розглянутому прикладі за рахунок збільшення товарної маси біржовий оборот зріс на 18%, зниження цін призвело до зменшення біржового обороту на 1,4%.

У межах індексної системи можна визначити також абсолютний вплив факторів на приріст результату. Абсолютний приріст біржового обороту

У нашому прикладі

= 27415 – 23550 = 3865 тис. грн.

Він спричинений обома факторами, тобто товарною масою і цінами :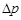

Абсолютний вплив кожного фактора окремо визначається як різниця між чисельником і знаменником відповідного індексу:

,

.

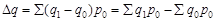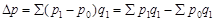Згідно з даними табл. 9.2, тис. грн.:

,

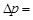27415 – 27800 = – 385.

Разом: 3865.

Якщо абсолютний вплив факторів односпрямований, можна визначити питому вагу кожного фактора. При різноспрямованих впливах такі розрахунки не мають сенсу.

Коли факторів три і більше, передусім необхідно визначити їх послідовність, ураховуючи суть кожного з них, порядок розрахунку, взаємозв’язок у системі. Наприклад, y = abc. Припустимо, що результативний показник у — відносна величина. Тоді першим фактором-співмножником буде той, чисельник розрахункової формули якого є чисельником результативного показника; у наступного фактора-співмножника чисельник розрахункової фор­мули є знаменником першого фактора і т. д.

Наприклад, y — прибутковість власного капіталу фірми, a — при­бутковість поточних активів, b — коефіцієнт поточної ліквідності, c — частка поточних пасивів у власному капіталі. Згідно з розрахунковими формулами послідовність факторів у системі така:

Отже, Ваги в індексах-співмножниках фіксуються за схемою: в індексі першого фактора — на рівні базисного періоду, в індексі другого фактора — ті, що праворуч від індексованої величини, на рівні базисного періоду, ті, що ліворуч, — на рівні поточного періоду, в індексі третього фактора — усі ваги фіксуються на рівні поточного періоду (вони розміщені ліворуч від індексованої величини).

У символах система зважування факторів має такий вигляд:

.

Як і у двофакторній індексній системі, абсолютний вплив зміни будь-якого фактора на динаміку результату визначається як різниця між чисельником і знаменником відповідного індексу. Тотожні оцінки абсолютного впливу факторів дає ланцюговий метод, який ґрунтується на умовних значеннях результативного показника. Замінимо 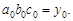Тоді 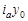— значення результативного показника за умови, що на динаміку останнього впливає лише фактор . Різниця характеризує абсолютний приріст 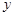за рахунок фактора . Аналогічно визначається абсолютний вплив інших факторів:

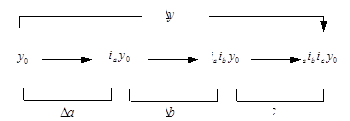
Очевидно, що

Наприклад, прибутковість власного капіталу зменшилась з 32% у базисному періоді до 24% у поточному, тобто на 8 п. п. Індекс прибутковості становить І_у = 24: 32 = 0,75. За той же період прибутковість активів зменшилась на 10%, поточна ліквідність — на 15%, частка поточних пасивів у власному капіталі — на 2%.

Індексна система має вигляд:

0,90 · 0,85 · 0,98 = 0,75.

Розрахунок абсолютного впливу факторів на динаміку прибутковості капіталу подано в табл. 9.5.

Таблиця 9.5

АБСОЛЮТНИЙ ВПЛИВ ФАКТОРІВ НА ЗМЕНШЕННЯ
ПРИБУТКОВОСТІ ВЛАСНОГО КАПІТАЛУ

Фактор	Індекс	Розрахункова величина	Абсолютний вплив фактора, п.п.
а	0,90	32,0 · 0,90 = 28,8	28,8 – 32,0 = –3,2
b	0,85	28,8 · 0,85 = 24,5	24,5 – 28,8 = –4,3
с	0,98	24,5 · 0,98 = 24,0	24,0 – 24,5 = –0,5
Разом	´	´	–8,0

За даними таблиці найвагоміший вплив на зменшення прибутковості капіталу виявив фактор b — поточна ліквідність.

5. Індекси середніх величин

Поряд зі зведеними, агрегатними індексами в статистичній практиці широко використовують індекси середніх величин (індекси середньої заробітної плати, середньої врожайності тощо). Як відомо, рівень середньої залежить від значень ознаки х_j і структури сукупності:

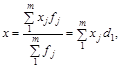
де f_j — частота; d_j — частка j- ї складової сукупності.

Очевидно, що й динаміка середньої визначається цими факторами: а) зміною значень ознаки x_j і б) структурними зрушеннями. Вплив кожного з них на динаміку середньої оцінюється за допомогою системи індексів середніх величин: змінного й фіксованого складу, а також структурних зрушень. У наведених формулах індексів ідентифікація складових сукупності відсутня.

Індексом змінного складу називають індекс середньоївеличини, він відбиває не лише зміни значень ознаки х, а й зміни в структурі сукупності:

.

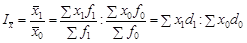В індексі фіксованого складу 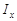ваги постійні, тобто усувається вплив на динаміку середньої структурних зрушень. Величина 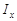показує, як у середньому змінилися значення ознаки при незмінній, фіксованій структурі:

Індекс структурних зрушень I_d, навпаки, показує, як змінилася середня за рахунок структурних зрушень; значення ознаки x фіксуються на постійному рівні:

У кожній конкретній індексній системі I_d оцінює вплив на динаміку середньої того структурного фактора, який є основою поділу сукупності на складові.

Формули індексів фіксованого складу і структурних зрушень різнозважені: в I_x ваги фіксуються на рівні поточного періоду, в I_d — значення ознаки x — на рівні базисного періоду. Саме такий варіант зважування забезпечує пов’язування цих індексів у систему:

Розглянемо побудову індексів середніх величин на прикладі трудомісткості продукції одного виду, яка виготовляється за різними технологіями (табл. 9.6).

Таблиця 9.6

ДО РОЗРАХУНКУ ІНДЕКСІВ СЕРЕДНІХ ВЕЛИЧИН

Технологія	Виробництво продукції, шт.	Затрати праці на один виріб, людино-год	ix	Розрахункові величини
Базисний пріод f 0	Поточний період f 1	Базисний період x 0	Поточний період x 1	x 0 f 0	x 0 f 1	x 1 f 1
А			2,0	1,8	0,900
Б			2,8	2,5	0,893
Разом			´	´	´

За поточний період затрати праці на виготовлення одного виробу зменшилися: за технологією А — на 10% (= 0,900), за технологією Б — на 10,7% (i_x = 0,893). Водночас змінилася структура виробництва: на 20 п. п. зросла частка виробництва за менш трудомісткою технологією А, на стільки ж пунктів зменшилася частка виробництва за технологією Б. Середні затрати праці на один виріб у базисному періоді людино-год, у поточному 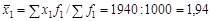людино-год, тобто змен­шилися на 16,4%:

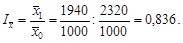
Індекс змінного складу значно менший за індивідуальні індекси затрат праці. Такий парадоксальний результат пояснюється тим, що на динаміку середньої вплинула не лише динаміка трудомісткості виробу по окремих технологіях, а й структурні зрушення в обсягах виробництва.

Зафіксувавши структуру виробництва на одному й тому самому рівні (поточному), визначимо, як у середньому змінилася трудомісткість продукції. Індекс фіксованого складу

тобто в середньому затрати праці на виробництво одного виробу зменшилися на 10,2%.

Індекс фіксованого складу I_x тотожний середньозваженому гармонічному індексу з індивідуальних індексів затрат праці з поточними вагами:

За рахунок структурних зрушень, а саме збільшення обсягів виробництва за менш трудомістською технологією А, середня трудомісткість виробництва зменшилася на 6,9%:

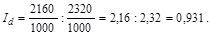
Система індексів середніх величин має вигляд:

.

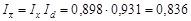У рамках індексної системи можна визначити абсолютні прирости середньої за рахунок кожного фактора: =
= 1,94 – 2,32 = – 0,38 людино-год, у тому числі за рахунок трудомісткості окремих технологій 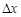= 1,94 – 2,16 = – 0,22, за рахунок структурних зрушень = 2,16 – 2,32 = – 0,16.

Методологічною особливістю побудови системи індексів середніх величин є порівнянність складових сукупності в часі. Проте більшість реальних сукупностей за своїм складом динаміч­ні: одні частини сукупності зникають, інші (нові) — з’являються. Так, оновлюється асортимент продукції, на ринку цінних паперів з’яв­ляються нові емітенти, у видобувній промисловості вводяться в експлуатацію нові родовища і т. ін.

Щоб оцінити вплив на динаміку середньої такого роду змін, в індексну систему вводять три індекси структурних зрушень: — для оцінювання впливу змін у структурі порівнянного кола складових сукупності; 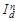— для оцінювання впливу новоутворених складових, — для оцінювання впливу вибулих складових. Індексна система має вигляд

.

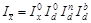Індекс фіксованого складу обчислюється для порівнянного кола складових. Вагами всіх індексів є відносні величини структури — частки .

Отже,

;

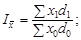
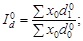
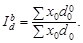
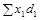Наприклад, на ринку пального діють чотири постачальники високооктанового автобензину: A, B, C, D. У березні постачальниками A, B, C поставлено 250 тис. т бензину, у квітні постачальниками A, B, D — 300 тис. т. Ціни на автобензин у постачальників різні (табл. 9.7). Середня ціна 1 тонни автобензину в березні становила = 324,5 грн., у квітні — = 314,6, що на 3% менше:

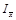= = 314,6: 324,5 = 0,970.

Постійними на ринку були постачальники A і B. У квітні вони знизили ціну на автобензин у середньому на 2,1%, індекс фіксованого складу

Таблиця 9.7

ДО РОЗРАХУНКУ СИСТЕМИ ІНДЕКСІВ СТРУКТУРНИХ ЗРУШЕНЬ

Постачальники	Ціна 1 т, грн.	Обсяг поставок, тис.т	Частка поставки
Березень	Квітень	Березень	Квітень	у загальному обсязі	по порівнянному колу
х 0	х 1	f 0	f 1	d 0	d 1
А					0,48	0,47	0,60	0,70
В					0,32	0,20	0,40	0,30
С		—		—	0,20	—	—	—
D	—		—		—	0,33	—	—
разом	´	´			1,0	1,0	1,0	1,0

За рахунок структурних зрушень в обсягах поставки постійних постачальників середня ціна автобензину зменшилася на 0,2%:

.

Вихід з ринку автобензину постачальника C з відносно низькою ціною призвів до збільшення середньої ціни на 0,6%:

.

Поява на ринку нового постачальника D з найнижчою ціною спричинила зниження середньої ціни на 1,3%:

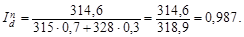
Очевидний взаємозв’язок індексів

Отже, динаміка середньої ціни на автобензин формувалася за рахунок як динаміки цін в окремих постачальників, так і різно-
спрямованої дії структурних факторів.

Дата добавления: 2014-01-07