Кількісне вимірювання інформації. Ентропія повідомлення

ПМС ТЕЗ 200 р. протокол №.

Методична розробка обговорена на засіданні

Редагування систематичного каталогу

Для того, щоб систематичний каталог відповідав названим вимогам, у бібліотеках має постійно проводитись робота щодо його удосконалення, враховуючи нові досягнення науки і техніки, зміни, що відбуваються у суспільно-політичному і культурному житті тощо. З цією метою здійснюють редагування систематичного каталогу. Головними напрямками при цьому є редагування змісту, структури і оформлення каталогу. У процесі редагування змісту перевіряють відповідність вміщених у розділі видань його змісту, виявляють застарілі видання, виправляють помилки, допущені у процесі систематизації. Редагуючи структуру систематичного каталогу, бібліотекар створює нові розділи для актуальних питань. Може бути прийняте рішення про використання більш дрібних ділень, особливо, коли за окремими розділовими картками збирається велика кількість карток, у процесі редагування перевіряють також оформлення розділових карток та його зовнішнє оформлення. Усі зміни і доповнення, що вносять до систематичного каталогу, мають знайти відтворення в АПП, а також у робочих таблицях класифікації.

Мета заняття: вивчити основи кількісного вимірювання інформації в каналах дискретних та неперервних повідомлень.

Час: 2 години.

Місце заняття: навчальна аудиторія.

Навчальні питання заняття:

1. Кількісне вимірювання інформації. Ентропія повідомлення.

2. Поняття про надлишковість повідомлень.

Матеріальне забезпечення:

Плакат: Ймовірності літер української мови.

Література:

1. Бабич В. Д., Кувшинов О. В., Лівенцев С. П. Основи теорії інформації. 2000. с. 4-15.

ЗМІСТ ЛЕКЦІЇ

Основним функціональним призначенням будь-якої системи передачі є передача каналами цієї системи інформації за допомогою електричних сигналів. У процесі передачі каналами електрозв'язку сигнали піддаються численним перетворенням, які істотно змінюють їх фізичні характеристики. При цьому втрачається частина переданої каналом інформації. Для порівняння між собою різноманітних джерел повідомлень, каналів електрозв'язку і систем передачі необхідно ввести кількісну міру інформації.

Будь-яке повідомлення, що підлягає передачі, має свій зміст і визначену цінність для одержувача. Проте, усе це несуттєво для зв'язку і тому не враховується при кількісному визначенні інформації.

При вимірюванні кількості інформації враховуються лише статистичні характеристики переданих повідомлень. Важливою властивістю інформації є те, що кожне повідомлення завжди вибирається з деякої множини (ансамблю) можливих повідомлень. Наприклад, кількість інформації в телеграмі визначається не тільки кількістю слів, які містяться у ній, але і тим, з якого набору можливих слів вона складена. Нехай відправник має у своєму розпорядженні вибір зі слів «А» і «В». У цьому випадку відправник може скласти усього лише чотири телеграми з двома словами: АА, АВ, ВА, ВВ. Якщо мати три можливих слова А, В, С, можна скласти дев'ять телеграм з двома словами: АА, СС, АВ, АС, ВА, СА і т.д. У загальному випадку з m можливих слів можна скласти mⁿ телеграм з n слів у кожній.

Крім цього, при оцінці кількості інформації в телеграмі варто врахувати, що деякі слова при передачі використовуються рідше, деякі - частіше, тобто ймовірність вибору різних слів різноманітна. Так, якщо джерело є дискретним, то повідомлення є результатом вибору з m можливих для даного джерела елементів. Якщо усі вибори рівноймовірні, то кількість можливих повідомлень для такого джерела буде дорівнювати

. (10.1)

Процес приймання інформації можна розглядати як процес вибору даного повідомлення з множини М. Чим більше М, тим більше інформації ми одержуємо при передачі кожного повідомлення. Але саме число М ще не є зручною мірою кількості інформації, тому що не задовольняє природної вимоги адитивності, відповідно до якої кількість інформації повинна бути лінійною функцією n.

Відповідно до цієї вимоги в k разів більш «довге» повідомлення за інших рівних умов, повинно містити в k разів більшу кількість інформації.

Суворі методи кількісного визначення інформації були запропоновані К. Шенноном [37] у 1948 р. і призвели до побудови теорії інформації, яка є математичною основою теорії зв'язку, кібернетики і ряду інших наук.

Нехай деяке джерело дискретних повідомлень посилає одне конкретне повідомлення a £ A з деякого ансамблю A. Спробуємо знайти визначення кількості інформації, що міститься в цьому повідомленні, виходячи з таких природних вимог:

1. Кількість інформації повинна бути адитивною мірою, тобто кількість інформації в двох незалежних повідомленнях повинна дорівнювати сумі кількостей інформації в кожному з них.

2. Кількість інформації в повідомленні про достовірну подію дорівнює нулю.

3. Кількість інформації не повинна залежати від якісного змісту повідомлення, зокрема, від ступеня його важливості для адресата, від можливих наслідків його передачі, від емоційного забарвлення тощо.

Перша вимога настільки природна, що не потребує додаткових обгрунтувань. Зауважимо лише, що мова йде про незалежні повідомлення, коли одержання одного з них ніяк не впливає на сприйняття іншого.

Другу вимогу також легко зрозуміти, оскільки повідомлення про достовірну подію не може нічого змінити в наших знаннях.

Третя вимога не здається настільки очевидною. Проте, вона обгрунтована необхідністю абстрагуватися від різноманітних несуттєвих деталей для того, щоб побудувати достатньо загальну теорію.

Наприклад, не можна було б побудувати наукову механіку, якщо по-різному визначати масу тіл, які складаються з різноманітних речовин.

Отже, для визначення кількості інформації в повідомленні необхідно спиратися тільки на такий параметр, який в самому загальному виді характеризує повідомлення a з ансамблю A. Важливою властивістю інформації є те, що кожне повідомлення завжди вибирається з деякої множини (ансамблю) можливих повідомлень. Причому ймовірність вибору різноманітних повідомлень у загальному випадку різноманітна.

Якщо передане повідомлення заздалегідь цілком точно відомо, то в звичайному значенні слова воно не несе ніякої інформації. Якщо деяка подія відома “майже напевно”, тобто ймовірність її близька до одиниці, то одержання повідомлення, яке підтверджує цю подію, приносить лише невелику інформацію. Навпаки, повідомлення про подію, що вважалася малоймовірною, є “сенсацією”, тобто воно несе багато інформації.

Із сказаного випливає: міру кількості інформації доцільно вибирати таким чином, щоб вона відображала ступінь новизни, оригінальності, неочікуваності даного повідомлення. Таким чином міра кількості інформації повинна визначатися не конкретним змістом повідомлення, а тією кількістю невизначеностей, які вирішуються при прийманні даного повідомлення. Виходячи з того, що перераховані властивості пов'язані тільки з ймовірністю появи повідомлення, можна вважати, що кількість інформації I (a), яка міститься в повідомленні “ a ”, повинна бути функцією його ймовірності P (a)

I (a) = I (P (a)). (10.2)

Нехай a ₁, a ₂ - два незалежних повідомлення. Ймовірність того, що джерело відправить обидва ці повідомлення (одне за іншим), дорівнює P (a ₁, a ₂) = P (a ₁) P (a ₂), а інформація, яка міститься в них, повинна задовольняти умові адитивності, тобто

I (a ₁, a ₂) = I (a ₁) + I (a ₂). (10.3)

Отже, необхідно знайти функцію від ймовірності P, яка володіє такою властивістю, що при перемноженні двох аргументів значення функції складаються.

У 1928 р. Хартлі запропонував застосувати логарифмічну функцію М як кількісну міру інформації.

Якщо М - число можливих повідомлень, то кількість інформації, що міститься в повідомленні, буде дорівнювати

. (10.4)

Ця функція найбільш зручна і ближче до наших інтуїтивних уявлень про кількісну міру. Вона більш зручна і з математичної точки зору.

Найпростішим випадком є вибір з двох рівноймовірних можливостей: «так» або «ні». Кількість інформації, що передається в цьому випадку, зручно прийняти за одиницю інформації. Тут М = 2 (m = 2, n = 1) і якщо основа логарифма також дорівнює 2, то одержимо величину . Цю одиницю прийнято називати «біт» або «двійковою одиницею». Така одиниця на практиці є найбільш зручною внаслідок широкого використання двійкових кодів в обчислювальній техніці і зв'язку. У теоретичних дослідженнях іноді застосовують натуральний логарифм (нат) або десятковий (діт).

Надалі позначення log буде означати двійковий логарифм.

Отже кількість інформації в повідомленні тим більша, чим менш воно ймовірно, тобто чим воно більш неочікуване.

Кількість інформації в одному елементі повідомлення, визначається як

. (10.5)

Відповідно до прийнятого вище означення, обчислення кількість інформації знаходиться як логарифм числа можливих виборів (повідомлень). При цьому вважають, що усі вибори рівноймовірні і незалежні. Ймовірність передачі кожного можливого повідомлення а в цьому випадку буде ,

а кількість інформації

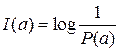. (10.6)

З формули (10.6) випливає, що повідомлення має тим більшу кількість інформації, чим менша його апріорна ймовірність. Це положення узгоджується з нашими звичайними уявленнями про інформацію. До передачі повідомлення а про якусь подію має місце невизначена ситуація, що характеризується ймовірністю можливих наслідків Р (а). З одержанням повідомлення ця невизначеність знімається. Очевидно, чим більша невизначеність мала місце до передачі повідомлення, тим більшу кількість інформації ми одержуємо при її знятті. Можна сказати, що кількість інформації вимірюється ступенем невизначеності сукупності можливих повідомлень.

Взагалі, при передачі повідомлення невизначеність знімається не повністю. Так, при передачі каналом із завадами (шумами) можливі помилки. Після одержання інформації залишається деяка невизначеність, але вона менша від тієї невизначеності, що була до передачі повідомлення.

Отже, кількість інформації, що міститься в даному повідомленні, вимірюється ступенем зменшення невизначеності при передачі останнього. Виходячи з цього, формулу (10.6) варто переписати в більш загальному вигляді

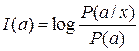, (10.7)

де Р (а / х) - апостеріорна ймовірність повідомлення, що характеризує невизначеність ситуації після одержання повідомлення,

Р (а) - апріорна ймовірність, що характеризує невизначеність ситуації до передачі повідомлення.

При розв’язуванні більшості практичних задач необхідно знати середню кількість інформації, що приходиться на одне повідомлення (на один символ повідомлення).

У тому випадку, якщо джерело повідомлення видає рівноймовірні і статистично незалежні символи, маємо

, (10.8)

де Н - змістовність або ентропія джерела повідомлень.

Нехай дискретне джерело видає послідовності символів довжиною n з алфавітом обсягом m. Тоді кількість можливих послідовностей довжиною n дорівнює . Нехай задані ймовірності появи цих послідовностей . Кількість інформації, яка міститься в послідовності довжини n дорівнює 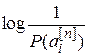і є випадковою величиною.

Припустимо, що всі повідомлення незалежні і несумісні, крім цього 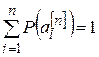. Останнє означає, що завжди передається одне з цих повідомлень. У випадку, коли в каналі шуми відсутні, приймач завжди приймає повідомлення безпомилково (Р (а / х) = 1) і відповідно до виразу (10.7) кількість інформації, що несе повідомлення а_i, дорівнює

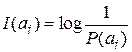. (10.9)

З формули (10.9) випливає, що в скінченному ансамблі А різноманітні повідомлення несуть різну кількість інформації. Менш ймовірні повідомлення несуть велику кількість інформації і, навпаки.

У цьому випадку відповідно до правил теорії імовірностей середня кількість інформації, що міститься в одному символі, дорівнює математичному очікуванню величини I (a_i), тобто

або, з урахуванням (10.9),

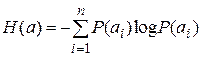. (10.10)

Величина H (а) називається ентропією джерела повідомлень, що характеризує міру невизначеності сукупності повідомлень даного джерела.

Легко помітити, що вираз (10.8) є окремим випадком формули (10.10) при .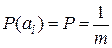

Розглянемо ансамбль двох повідомлень а ₁ і а ₂ з апріорними ймовірностями і . У цьому випадку

. (10.11)

На рис. 10.1 наведено графік залежності Н (а) від р. З цього графіка випливає, що Н (а) має максимальне значення при 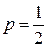, тобто коли ситуація є найбільш невизначеною. При р = 1 і р = 0 ентропія Н (а) дорівнює нулю.

У цих випадках невизначеність відсутня: при р = 1 передається повідомлення а ₁ і при р = 0 передається повідомлення а ₂.

Відповідно до виразу (10.11), H (a) = 0 лише в тому випадку, коли всі ймовірності , крім однієї, дорівнюють нулю, а ця єдина ймовірність дорівнює одиниці. При заданому n функція H (a) максимальна і дорівнює 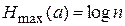тоді, коли всі повідомлення рівноймовірні, тобто

,

що відповідає найбільшій невизначеності.

Досі ми оцінювали статистичні властивості джерела повідомлень, з огляду тільки на розподіл ймовірностей окремих повідомлень (елементів повідомлення), вважаючи, що ці ймовірності незалежні.

Таким чином, ентропія - це середня кількість інформації, що міститься в одному символі послідовності джерела при необмеженому збільшенні довжини цієї послідовності.

.

Якщо повідомлення джерела нерівноймовірні і залежні, то з формули (10.13) можна одержати

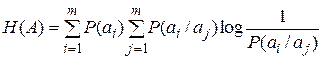, (10.14)

де P (a_i / a_j) - умовна ймовірність появи символу (повідомлення) a_i, якщо попереднім символом був a_j;

P (a_j) - безумовна ймовірність появи символу a_j.

З виразів (10.8, 10.10, 10.14) випливає, що чим більша ентропія джерела, тим більший у середньому ступінь неочікуваності переданих їм повідомлень, тобто тим більш невизначеним є очікуване повідомлення.

Таким чином можна сформулювати основні властивості ентропії.

1. Ентропія - величина невід’ємна. Вона дорівнює нулю тільки для ансамблю, коли одне повідомлення передається з ймовірністю 1, а інші - з ймовірністю 0.

2. Ентропія адитивна.

3. Якщо ансамбль містить N = mⁿ різноманітних повідомлень, то H (A) £ log N, причому максимальна ентропія H _max(A) = log N, має місце тільки тоді, коли всі повідомлення передаються рівноймовірно і незалежно.

Дата добавления: 2014-01-07