
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Колебания и волны
|
|
|
|
Лекция №1
- Гармонический осциллятор. Колебательные системы в биологии и медицине.
- Механические волны, их уравнение. Вектор Умова. Ультразвук, его применение в медицине.
- Эффект Доплера, его медицинские приложения
Колебания гармонического осциллятора являются очень важным примером периодического движения. К числу классических систем, аналогичных гармоническому осциллятору, относятся любые системы, которые, будучи слегка выведены из положения равновесия, совершают устойчивые колебания. К ним относятся:
- Математический маятник в пределах малых углов отклонения.
- Масса на пружине в пределах малых амплитуд колебаний
- Колебательный контур, состоящий из конденсатора и катушки
Частота колебаний осциллятора не зависит от амплитуды.
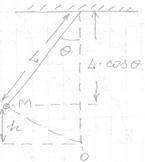
Математический маятник состоит из материальной (.) массой m, расположенной на нижнем конце невесомого стержня длиной L, свободно вращающегося вокруг оси, проходящей через верхний конец.
Выведем уравнение колебаний маятника. Проще всего записать уравнение F=ma, однако поучительнее будет решить поставленную задачу через закон сохранения энергии. Отклонение маятника определяется углом  , который стержень образует с вертикалью.
, который стержень образует с вертикалью.
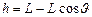 (1)
(1)
Потенциальная энергия маятника
U(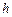 )=Mgh (2)
)=Mgh (2)
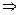
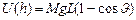 (3)
(3)
Кинетическая энергия маятника равна
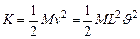 (4)
(4)
Полная энергия маятника равна 
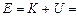
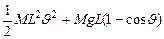 (5)
(5)
Принимая во внимание, что 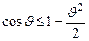 (6),
(6),
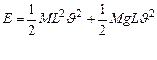 (7)
(7)
Решая это уравнение относительно  находим
находим
 (8)
(8)
При 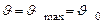
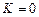 . Тогда из (7) получим с учетом того, что
. Тогда из (7) получим с учетом того, что  :
:
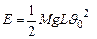 ,
, 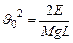 (9)
(9)
Тогда (8) перепишется в виде:
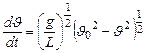 (10)
(10)
Или 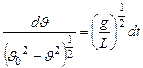 (11)
(11)
Этот вид удобен для интегрирования. Если начальные условия Иаковы, что при 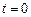
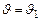 , то
, то
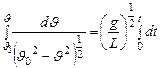 (12)
(12)
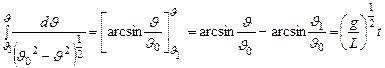 (13)
(13)
Так как 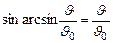 , то (13) запишется
, то (13) запишется 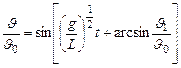 (14)
(14)
Или 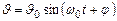 (15)
(15)
Где 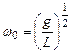 -круговая частота
-круговая частота
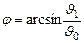 -фаза
-фаза
Период колебаний математического маятника 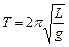
пружинного 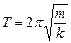
колебательного контура 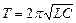
Примеры решения задач
Материальная точка массой 5 г. колеблется согласно уравнению 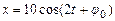 . Найти максимальную силу, действующую на точку и полную энергию.
. Найти максимальную силу, действующую на точку и полную энергию.
Решение
Сила, действующая на матер. точку, равна 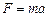 . Ускорение
. Ускорение 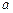 может быть найдено как вторая производная смещения
может быть найдено как вторая производная смещения 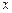 по времени. Первая производная
по времени. Первая производная 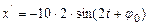 . Вторая производная
. Вторая производная 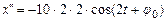 . Максимальное значение косинуса -1,
. Максимальное значение косинуса -1, 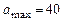 и
и 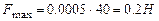

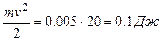
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 286; Нарушение авторских прав?; Мы поможем в написании вашей работы!