
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Волновые свойства света
|
|
|
|
1. Интерференция света.
2. Дифракция света. Разрешающая способность оптических приборов.
3. Дифракция от одной щели. Дифракционные спектры. Дифракционная решетка.
1. Под интерференцией света называют такое наложение световых волн от когерентных источников, в результате которого образуется устойчивая картина их взаимного усиления или ослабления.
Когерентные источники света – это такие источники, которые излучают с постоянной разностью фаз.
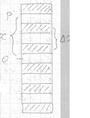
Естественных когерентных источников света в природе не существует, поскольку свет, исходящий от светящегося тела, представляет собой совокупность множества электромагнитных волн, излучаемых отдельными частицами (атомами и молекулами тела), условия излучения которых непрерывно и беспорядочно изменяются. Поэтому для получения когерентных источников прибегают к искусственному приему: «раздваивают» свет, исходящий от источника, например, посредством экрана с двумя малыми отверстиями.
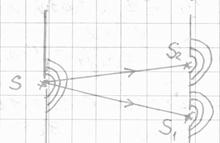
В соответствии с принципом Гюйгенса-Френеля источник света S создает в отверстиях экрана вторичные источники света S1 и S2, которые являются когерентными.
Другой способ получения когерентных источников основан на отражении света от двух плоских зеркал (зеркал Френеля), установленных под углом 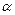 , близким к 180 º. Когерентными источниками служат изображения S1 и S2 основного источника света S.
, близким к 180 º. Когерентными источниками служат изображения S1 и S2 основного источника света S.
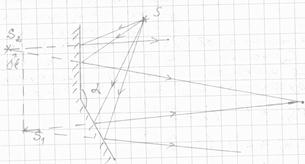
Результат интерференции двух волн в некоторой точке Р зависит от величины разности хода лучей. Интерференционные max и min наблюдаются при следующих условиях.
Если разность хода лучей 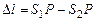 укладывается целое число волн (четное число полуволн), т.е.
укладывается целое число волн (четное число полуволн), т.е. 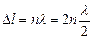 (1).
(1).
То в точке Р будет максимум света (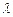 -длина волны, n=0. 1. 2. 3). Если же в разности хода лучей укладывается нечетное число полуволн, т.е. если
-длина волны, n=0. 1. 2. 3). Если же в разности хода лучей укладывается нечетное число полуволн, т.е. если  (2),
(2),
То в точке Р будет минимум света (темнота)
Выясним, как выглядит интерференционная картина, создаваемая на экране двумя когерентными источниками монохроматического света S1 и S2. Пусть расстояние между этими источниками d, а расстояние от источников до экрана L, причем d<<L. Определим расстояние х от точки О (одинаково удаленной от S1 и S2) до тех точек Р, в которых будут наблюдаться интерференционные макимумы.
Из прямоугольных треугольников PCS1 и PBS2 находим:
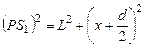
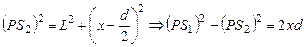 или
или
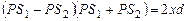 но
но 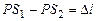 , а
, а 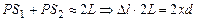 и
и
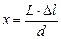 (3)
(3)
Учитывая формулы (1) и (2), получим, что максимумы света располгаются на расстоянии
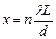 (4)
(4)
А минимумы на расстоянии 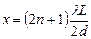 (5)
(5)
Эти максимумы и минимумы имеют соответственно вид светлых и темных полос, параллельных друг другу. Центральный максимум соответствующий n=0, проходит через точку О. Расстояние между соседними максимумами (или минимумами), очевидно, равно
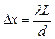 (6)
(6)
Таким образом, интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос.
На основании формулы (6) можно экспериментально определить длину световой волны по измеренным значениям d, L и 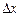 .
.
2. Явление прямолинейного распространения света вблизи преграды (огибание световым лучом преграды) называется дифракцией света. При использовании белого света дифракционная картина приобретает радужную окраску.
Дифракцией света обусловлена разрешающая сила (способность) оптических приборов, т.е. способность этих приборов давать раздельное изображение мелких, близко расположенных друг к другу деталей (точек) предмета.
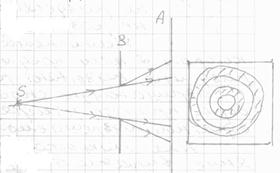
Объектив всякого оптического прибора обязательно имеет входное отверстие. Дифракция света на входном отверстии объектива неизбежно ведет к тому, что изображения отдельных точек наблюдаемого предмета оказываются уже не точками, а светлыми дисками, окаймленными темными и светлыми кольцами. Если рассматриваемые точки (детали) предмета находятся близко друг от друга, то их дифракционные изображения (в фокальной плоскости объектива) могут более или менее перекрываться.
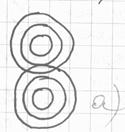
Две близкие точки предмета можно еще видеть раздельно, если световые диски их дифракционных изображений взаимно перекрываются не более чем на величину радиуса диска.(а)
Если же диски перекрываются более чем на радиус (б), то раздельное видение точек становиться невозможным; прибор уже не разделяет, или, как говорят, не разрешает, таких точек.

Наименьшее расстояние 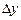 , при котором две точки предмета еще можно видеть раздельно, называют разрешающим расстоянием.
, при котором две точки предмета еще можно видеть раздельно, называют разрешающим расстоянием.
Разрешающую способность оптического прибора принято измерять величиной 1/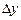 , обратной разрешаемому расстоянию.
, обратной разрешаемому расстоянию.
Для микроскопа разрешаемое расстояние выражается формулой
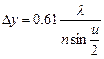 (7)
(7)
Где 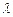 -длина волны света, n –показатель преломления среды, находящейся между предметом и объективом, u- апертурный угол, т.е. угол, образованный крайними лучами светового пучка, попадающего в объектив.
-длина волны света, n –показатель преломления среды, находящейся между предметом и объективом, u- апертурный угол, т.е. угол, образованный крайними лучами светового пучка, попадающего в объектив.
Произведение 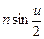 называется числовой апертурой.
называется числовой апертурой.
Согласно (7), разрешающая способность микроскопа 1/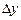 пропорциональна числовой апертуре и обратно пропорциональна длине волны света. Следовательно, для повышения разрешающей способности микроскопа необходимо увеличить его числовую апертуру, так как
пропорциональна числовой апертуре и обратно пропорциональна длине волны света. Следовательно, для повышения разрешающей способности микроскопа необходимо увеличить его числовую апертуру, так как 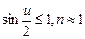 , то числовую апертуру можно несколько увеличить, если предмет поместить в иммерсионную жидкость, например, в глицерин (n=1.47) или кедровое масло (n=1,52).
, то числовую апертуру можно несколько увеличить, если предмет поместить в иммерсионную жидкость, например, в глицерин (n=1.47) или кедровое масло (n=1,52).
Т.о., числовая апертура микроскопа ~1, а из (7) следует, что 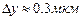 (если полагать, что
(если полагать, что  =0,5мкм). Это означает, что в оптический микроскоп нельзя рассматривать предметы, размер которых меньше 0,3мкм.
=0,5мкм). Это означает, что в оптический микроскоп нельзя рассматривать предметы, размер которых меньше 0,3мкм.
Разрешающая способность ставит предел полезному увеличению микроскопа. При увеличении порядка 103 разрешающему расстоянию(0,3мкм) соответствует достаточно крупное изображение (0,3мм). Добиваться большего увеличения не имеет смысла.
Одним из способов уменьшения предела разрешения микроскопа –использование света с меньшей длиной волны. В вязи с этим применяют ульрафиолетовый микроскоп, в котором микрообъекты исследуются в ультрафиолетовых лучах. Так как глаз непосредственно не воспринимает этого излучения, то употребляются фотопластинки, люминесцентные экраны или электронно-оптические преобразователи.
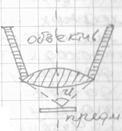
3. В лабораторной практике дифракционную картину получают обычно от узких светящихся щелей.
Пучок параллельных монохроматичесих лучей, проходя через линзу фокусируется в точке О, давая светлую полосу.
Учтем теперь, что благодаря дифракции лучи от щели пойдут не только в первоначальном направлении, но и под различными углами  к этому направлению (
к этому направлению ( -угол дифракции)
-угол дифракции)
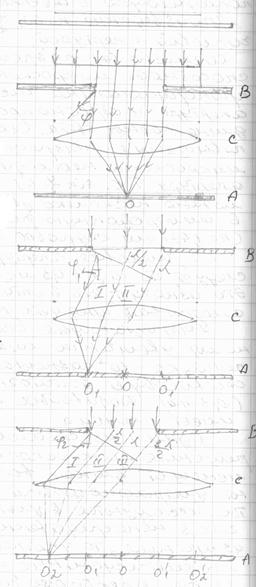
Рассмотрим пучок лучей, дифрагирующих от щели под таким углом 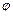 =
=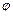 1, что разность хода
1, что разность хода 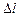 между крайними лучами пучка будет равна длине световой волны
между крайними лучами пучка будет равна длине световой волны 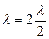
Тогда весь пучок можно разделить на такие 2 равные зоны 1 и 2, называемые зонами Френеля, для которых разность хода между каждым лучом первой зоны и соответствующим лучом второй зоны окажется равной 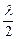
Будучи собраны линзой на линии, проходящей через точку О1, эти лучи проинтерферируют и взаимно погасятся. В результате через О1 пройдет темная полоса-дифракционный минимум. Такой же дифракционный минимум пройдет через О’1, симметричную О1.
Рассмотрим другой пучок лучей, дифрагирующих под таким углом 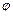 =
=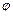 2, что разность хода
2, что разность хода 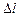 между крайними лучами пучка равна 3
между крайними лучами пучка равна 3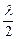 . Тогда весь пучок можно разделить на три зоны Френеля:1,2 и 3. Соседние зоны погасят друг друга (1и2), так как разность хода между лучами этих зон равна
. Тогда весь пучок можно разделить на три зоны Френеля:1,2 и 3. Соседние зоны погасят друг друга (1и2), так как разность хода между лучами этих зон равна 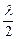 ), а третья зона останется непогашенной и даст дифракционный максимум на линии проходящей через О2. Такой же максимум появится на линии, проходящей через точку О’2.
), а третья зона останется непогашенной и даст дифракционный максимум на линии проходящей через О2. Такой же максимум появится на линии, проходящей через точку О’2.
Таким образом, пучки лучей, дифрагирующих под углами, соответствующими нечетному числу зон Френеля, создают на экране дифракционные максимумы, а пучки лучей, дифрагирующих под углами, соответствующими четному числу зон Френеля, создают дифракционные минимумы. Освещенность максимумов уменьшатся при увеличении участка дифракции лучей, создающих эти максимумы.
Таким образом, дифракционная картина, получаемая от одной из щелей, представляет собой чередующиеся темные и светлые полосы, симметрично расположенные по обе стороны от центрального максимума.
Освещенность светлых полос быстро убывает при увеличении ула дифракции лучей.
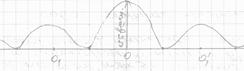
Дифракционные максимумы получаются при разности хода лучей
 . А дифракционные минимумы при
. А дифракционные минимумы при 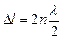 , Поскольку
, Поскольку , где а-ширина щели, то дифракционные максимумы наблюдаются под углами, для которых
, где а-ширина щели, то дифракционные максимумы наблюдаются под углами, для которых
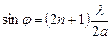 , а дифракционные минимумы под углами, для которых
, а дифракционные минимумы под углами, для которых
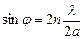
При использовании белого света каждый максимум (кроме центрального) приобретает радужную окраску. Дифракционные максимумы называют дифракционными спектрами, а число n –порядком спектра.
Совокупность большого числа узких параллельных щелей, расположенных близко друг от друга, называется дифракционной решеткой, а расстояние d между соседними щелями – периодом решетки.

Посредством дифракционной решетки проводятся очень точные измерения длины световых волн. Для этого пользуются дифракционным спектром.
Примеры решения задач
1. В опыте с зеркалами Френеля расстояние между мнимыми изображениями источника света равно d=0,5мкм, расстояние до экрана L=5м. В зеленом свете на экране получились интерференционные полосы на расстоянии 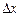 =5мм друг от друга. Найти длину волны
=5мм друг от друга. Найти длину волны 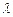 зеленого света.
зеленого света.
Решение:
Расстояние между соседними интерференционными полосами 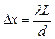 . Тогда
. Тогда 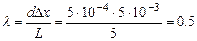 мкм.
мкм.
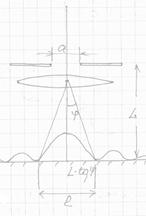
2. На щель шириной 0,1мм нормально падает параллельный пучок света от монохроматического источника (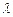 =0,6мкм). Определить ширину центрального максимума в дифракционной картине, проектируемой при помощи линзы, находящейся непосредственно за щелью, на экране, отстоящий от линзы на расстоянии L=1м.
=0,6мкм). Определить ширину центрального максимума в дифракционной картине, проектируемой при помощи линзы, находящейся непосредственно за щелью, на экране, отстоящий от линзы на расстоянии L=1м.
Решение: Максимумы интенсивности света при дифракции от одной щели наблюдаются под углами 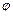 , определяемыми условиями
, определяемыми условиями 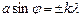 (1)
(1)
Расстояние между двумя минимумами 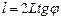
Так как при малых углах 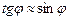
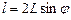 (2)
(2)
Выразим 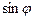 из (1) и подставим в (2), получим
из (1) и подставим в (2), получим
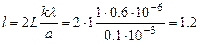 см
см
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 528; Нарушение авторских прав?; Мы поможем в написании вашей работы!