Коротші путі в графі

У реальних задачах на графах часто потрібно брати до уваги додаткову

інформацію — фактичну віддаль між окремими пунктами, вартість проїзду, час проїзду тощо. Для цього використовують поняття зваженого графа.

Зваженим називають простий граф, кожному ребру є якого приписано дійсне число w(e). Це число називають вагою ребра е. Аналогічно означають зважений орієнтований граф: це такий орієнтований граф, кожній дузі е якого приписано дійсне число w(e), називане вагою дуги.

Розглянемо три способи зберігання зваженого графа G = (V, Е) в пам'яті комп'ютера. Нехай , .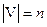

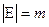Перший — подання графа матрицею ваг W, яка являє собою аналог матриці суміжності, її елемент 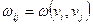, якщо ребро {v_i, v_j}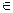Е (у разі орієнтованого графа — дуга 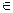Е). Якщо ж ребро {v_i, v_j}Е, то чи 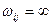залежно від розв'язуваної задачі.

Другий спосіб — подання графа списком ребер. Для зваженого графа під кожний елемент списку Е можна відвести три комірки — дві для ребра й одну для його ваги, тобто всього потрібно З m комірок.

Третій спосіб — подання графа списками суміжності. Для зваженого графа кожний список Adj [ u ] містить окрім покажчиків на всі вершини v; множини Г(u) ще й числа (u, v).

Довжиною шляху в зваженому графі називають суму ваг ребер (дуг), які утворюють цей шлях. Якщо граф не зважений, то вагу кожного ребра (кожної дуги) уважають рівною 1 й отримують раніше введене поняття довжини шляху як кількості ребер (дуг) у ньому.

Задача про найкоротший шлях полягає в знаходженні найкоротшого шляху від заданої початкової вершини а до заданої вершини z. Наступні дві задачі — безпосередні узагальнення сформульованої задачі про найкоротший шлях.

1. Для заданої початкової вершини а знайти найкоротші шляхи від а до всіх інших вершин.

2. Знайти найкоротші шляхи між усіма парами вершин.

Виявляється, що майже всі методи розв'язання задачі про найкоротший шлях від заданої початкової вершини а до заданої вершини z також дають змогу знайти й найкоротші шляхи від вершини а до всіх інших вершин графа. Отже, за їх допомогою можна розв'язати задачу 1 із невеликими додатковими обчислювальними витратами. З іншого боку, задачу 2 можна розв'язати або п разів застосувавши алгоритм задачі 1 із різними початковими вершинами, або один раз застосувавши спеціальний алгоритм.

Розглянемо два алгоритми: перший алгоритм призначений для розв'язування задачі 1, другий — для задачі 2.

Найефективніший алгоритм визначення довжини найкоротшого шляху від фіксованої вершини до будь-якої іншої запропонував 1959 р. датський математик Е. Дейкстра. Цей алгоритм застосовний лише тоді, коли вага кожного ребра (дуги) додатна. Опишемо докладно цей алгоритм для орієнтованого графа.

Нехай G = (V,E) — зважений орієнтований граф, — вага дуги . Почавши з вершини а, знаходимо віддаль від а до кожної із суміжних із нею вершин. Вибираємо вершину, віддаль від якої до вершини а найменша; нехай це буде вершина v. Далі знаходимо віддалі від вершини а до кожної вершини суміжної з v вздовж шляху, який проходить через вершину v*. Якщо для якоїсь із таких вершин ця віддаль менша від поточної, то заміняємо нею поточну віддаль. Знову вибираємо вершину, найближчу до а й не вибрану раніше; повторюємо процес.

Описаний процес зручно виконувати за допомогою присвоювання вершинам міток. Є мітки двох типів — тимчасові та постійні. Вершини з постійними мітками групують у множину М, яку називають множиною позначених вершин. Решта вершин має тимчасові мітки, і множину таких вершин позначимо як Т, Т=V\M. Позначатимемо мітку (тимчасову чи постійну) вершини v як l(v). Значення постійної мітки l (d) дорівнює довжині найкоротшого шляху від вершини a до вершини v, тимчасової — довжині найкоротшого шляху, який проходить лише через вершини з постійними мітками.

Фіксованою початковою вершиною вважаємо вершину а; довжину найкоротшого шляху шукаємо до вершини z (або до всіх вершин графа).

Алгоритм Дейкстри

Крок 1. Присвоювання початкових значень. Виконати l (a):=0 та вважати цю мітку постійною. Виконати l (d):=для всіх v а й уважати ці мітки тимчасовими. Виконати х:= а, М:={ а }.

Крок 2. Оновлення міток. Для кожної вершини v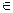Г(х)\М замінити мітки: l (d):=mm{ l (v); l (x) + 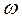(x, v)}, тобто оновлювати тимчасові мітки вершин, у які з вершини х іде дуга.

Крок 3. Перетворення мітки в постійну. Серед усіх вершин із тимчасовими мітками знайти вершину з мінімальною міткою, тобто знайти вершину v* з умови l (v*)=min{ l (v*)}, v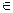Т, де Т=V\M.

Крок 4. Уважати мітку вершини v* постійною й виконати M:=M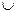{v*}; x:=v* (вершину v включено в множину М).

Крок 5. а) Для пошуку шляху від а до z: якщо x =z, то l (z) — довжина найкоротшого шляху від а до z, зупинитись; якщо xz, то перейти до кроку 2.

б) Для пошуку шляхів від а до всіх інших вершин: якщо всі вершини отримали постійні мітки (включені в множину М), то ці мітки дорівнюють довжинам найкоротших шляхів, зупинитись; якщо деякі вершини мають тимчасові мітки, то перейти до кроку 2.

Якщо граф подано матрицею суміжності, складність алгоритму Дейкстри становить 0{ п ²}. Коли кількість дуг m значно менша., ніж п ², то найкраще подавати орієнтований граф списками суміжності. Тоді алгоритм можна реалізувати зі складністю 0(m log n), що в цьому разі істотно менше, ніж 0(п²).

Ми розглянули задачу відшукання в графі найкоротшого шляху від якоїсь виділеної (початкової) вершини до будь-якої іншої. Розглянемо задач;' пошуку в графі найкоротшого шляху між кожною парою вершин. Звичайно, цю загальнішу задачу можна розв'язати багатократним застосуванням алгоритму Дейкстри з послідовним вибором кожної вершини графа як початкової. Проте є й прямий спосіб розв'язання цієї задачі за допомогою алгоритму Флойда. У ньому довжини дуг можуть бути від'ємними, проте не може бути циклів із від'ємною довжиною.

Нехай G= (V. Г) — орієнтований граф. Нагадаємо, що внутрішні вершини шляху а, х₁, х₂,..., х_т-1, b в графі G — х₁, х₂,..., х_{т- 1}. Наприклад, внутрішні вершини шляху а, с, d, a, f, b — с, d, a, f. Пронумеруємо вершини графа цілими числами від 1 до п. Позначимо як довжину найкоротшого шляху з вершиш і у вершину j, у якому як внутрішні можуть бути лише перші k вершин графа G. Якщо між вершинами і та j не існує жодного такого шляху, то умовно вважатимемо, що 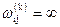. Зі сказаного випливає, що — це вага дуги (і,j), а якщо такої дуги немає, то . Для довільної вершини і вважатимемо 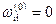. Отже 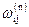дорівнює довжині наикоротшого шляху з вершини і у вершину j. Позначимо як 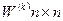матрицю (i,j)-й елемент якої дорівнює . Якщо в заданому орієнтованому графі G відома вага кожної дуги, то, виходячи з попередніх міркувань, можна сформувати матрицю 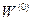. Тепер потрібно визначити матрицю 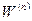, елементи якої дорівнюють довжинам найкоротших шляхів між усіма парами вершин графа G.

В алгоритмі Флойда як початкову беруть матрицю 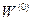. Спочатку за нею обчислюють матрицю , потім — 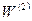, і процес повторюють доти, доки за матрицею не буде обчислено матрицю 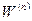. Розглянемо ідею, на якій грунтується алгоритм Флойда. Припустимо, що відомі.

1. Найкорогший шлях із вершини і у вершину k, у якому як внутрішні використано лише перші (k-1) вершин.

2. Найкоротший шлях із вершини k у вершину j, у якому як внутрішні використано лише перші (k-1) вершин.

3. Найкоротший шлях із вершини і у вершину j, у якому як внутрішні використано лише перші (k - 1) вершин.

Оскільки за припущенням граф G не містить циклів із від'ємною довжиною, то один із двох шляхів — шлях із п. З чи об'єднання шляхів із пп. 1 і 2 — найкоротший шлях із вершини і у вершину j, у якому як внутрішні використано лише перші (k-1) вершин. Отже,

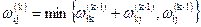(1)

Зі співвідношення видно, що для обчислення елементів матриці потрібні тільки елементи матриці 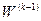. Тепер ми можемо формально описати алгоритм Флойда для знаходження в графі найкоротших шляхів між усіма парами вершин.

Алгоритм Флойда

Крок 1. Присвоювання початкових значень. Пронумерувати вершини графа G цілими числами від 1 до п. Побудувати матрицю 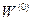=W. задавши кожний її (і, j)-елемєнт такий, що дорівнює вазі дуги. котра з'єднує вершину і з вершиною j. Якщо в графі G ці вершини не з'єднано дутою, то виконати . Крім того, для всіх і виконати .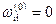

Крок 2. Цикл. Для k, що послідовно набуває значення 1, 2,..., п, визначити за елементами матриці 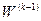елементи матриці , використовуючи рекурентне співвідношення (1).

Після закінчення цієї процедури (і, j)-елемент матриці 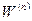дорівнює довжині найкоротшого шляху з вершини і у вершину j.

Якщо під час роботи алгоритму для якихось k й і виявиться, що, 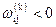, то в графі G існує цикл із від'ємною довжиною, який містить вершину і. Тоді роботу алгоритму потрібно припинити.

Якщо заздалегідь відомо, що в графі G немає циклів із від'ємною довжиною, то обсяг обчислень можна дещо зменшити. У цьому разі для всіх і та всіх k має бути 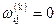. Тому не потрібно обчислювати діагональні елементи матриць , , 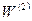…,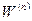. Окрім того, для всіх і=1,2, …п справджуються співвідношення 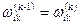, , які випливають із того, що коли немає циклів із від'ємною довжиною, вершина k не може бути внутрішньою в будь-яких найкоротших шляхах, котрі починаються чи закінчуються в самій вершині к. Отже, обчислюючи матрицю , немає потреби переобчислювати елементи k-то рядка й k-го стовпця матриці 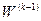. Отже, у матриці за формулою (1) потрібно обчислювати лише п²-Зп+2 елементи. Очевидно, що складність алгоритму Флойда становить 0(п³).

Дата добавления: 2014-01-07