Визначення графа

3. Способи завдання графів

4. Матриця інцидентності

5. Поняття маршруту і шляху

6. Зв'язність і компоненти

Елементи теорії графів

Останніми роками теорія графів отримала статус вельми актуальної галузі науки. З її допомогою представляється можливим вирішення великої кількості завдань з області економіки, техніки і безлічі інших сфер людської діяльності. Графи по суті є основними об'єктами, на яких будується сучасна теорія алгоритмів. Особливо важливий взаємозв'язок існує між теорією графів і теоретичною кібернетикою (особливо теорією автоматів, дослідженням операцій, теорією кодування, теорією ігор). Широко використовується теорія графів при вирішенні різних завдань на обчислювальних машинах. Достовірно і те, що теорія графів служить математичною моделлю для всякої системи, що містить бінарне відношення.

Визначення: Графом називається двоосновна модель <V, E; R >, де R – бінарне відношення множин V і E, таке, що кожен елемент e E знаходиться відносно R або рівно з одним, або рівно з двома елементами множини V. При цьому елементи множини V називаються вершинами графа, елементи безлічі E називаються ребрами графа, а відношення R – відношенням інцидентності. Вершини, інцидентні одному і тому ж ребру, називаються суміжними.

У деяких завданнях інцидентні ребру вершини неравноправни, вони розглядаються в певному порядку. Тоді кожному ребру можна приписати напрям від першої з інцидентних вершин до другої. Направлені ребра часто називають дугами, а граф, що містить їх, - орієнтованим або орграфом ( граф, визначений раніше, називається неорієнтованим). Перша по порядку вершина, інцидентна ребру орієнтованого графа, називається його початком, друга - його кінцем. Говорять ще, що ребро орієнтованого графа виходить з початку і входить в кінець.

Перша робота по теорії графів належить Леонарду Ейлерові (1736 рік), хоча термін «граф» вперше ввів в 1936 році угорського математика Денеш Кеніг.

Графи зазвичай зображаються у вигляді геометричних фігур, так що вершини графа зображаються крапками, а ребра – лініями, що сполучають ті крапки, відповідним вершинам яких ребра інцидентні, зазвичай граф позначають як G(V, E).

Пара вершин може бути сполучена двома або більш ребрами або дугами, такі ребра (або дуги) називаються кратними, а граф -мультіграфом. Дуга може починатися і закінчуватися в одній і тій же вершині, в цьому випадку відповідна дуга називається петлею.

Зупинимося докладніше на способах завдання графів. Це є важливим для їх уявлення при реалізації на ЕОМ алгоритмів, що застосовують графи як об'єкти програмування.

Задати граф - означає описати безліч його вершин і ребер, а також відношення інцидентності. Коли граф G - кінцевий, для опису його вершин і ребер досить їх занумерувати. Хай v1, v2..., vn - вершини графаg; e1, e2..., em - його ребра. Відношення інцидентності можна визначити матрицею ||ij ||, що має m рядків і n стовпців. Стовпці відповідають вершинам графа, рядки - ребрам. Якщо ребро ei інцидентно вершині Vj, то ij = 1, інакше ij = 0. Це так звана матриця інцидентності неорієнтованого графа G, яка є одним із способів його визначення (для неорієнтованого графа вона дана в табл. a).

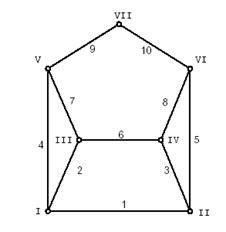
Мал. 1. Неорієнтований граф.

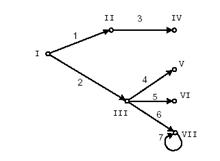
Мал. 2. Орієнтований граф.

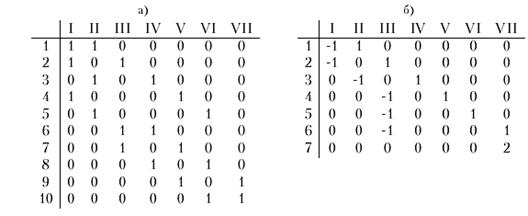У матриці інцидентності ||_ij || орієнтованого графа G, якщо вершина vj - начало ребра ai, то ij = -1; якщо vj - кінець ai, то ij = 1; якщо ai - петливши, а vj - інцидентна нею вершина, то ij = а, де а - будь-яке число, відмінне від 1, 0 і -1, у решті випадків ij = 0 (табл. б).

У кожному рядку матриці інцидентності для неорієнтованого або орієнтованого графа тільки два елементи відмінні від 0 (або один, якщо ребро є петлею). Тому такий спосіб завдання графа виявляється недостатньо економним. Відношення інцидентності можна ще задати списком ребер графа. Кожен рядок цього списку відповідає ребру, в ній записані номери вершин, інцидентних йому. Для неорієнтованого графа порядок цих вершин в рядку довільний, для орієнтованого першим коштує номер або інше найменування почала ребра, а другим - його кінця. У табл. у) і г) приводяться списки ребер для графів, зображених вище. За списком ребер графа легко побудувати його матрицю інцидентності. Дійсно, кожен рядок цього списку відповідає рядку матриці з тим же номером. Для неорієнтованого графа в рядку списку вказані номери елементів рядка матриці інцидентності, рівні 1, і для орієнтованого графа в цьому рядку першим коштує номер елементу рядка матриці, рівного -1, а другим - номер елементу, рівного +1.

Ще одним способом завдання графа є матриця суміжності - це квадратна матриця ||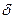_ij ||, стовпцям і рядкам якої відповідають вершини графа. Якщо існує ребро що зв'язує вершини vi і vj, то 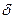_ij =1, інакше 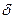_ij =0.

Матриці суміжності, розглянутих вище графів приведені в табл. д) і е)

д) е)

Матриця суміжності однозначно визначає структуру графа. Відзначимо, що петливши в матриці суміжності орієнтованого графа представляється відповідним одиничним діагональним елементом, а матриця суміжності неорієнтованого графа симетрична щодо головної діагоналі.

Ступінь вершини – число інцидентних цій вершині ребер, S(х).

Граф повний – граф G=(V, E), в якому будь-яка пара вершин інцидентна єдиному ребру. Позначається Kp, де р=|V|, при цьому | E |= p (p-1) /2.

Число ребер в графі обчислюється за формулою: n=p(p-1) /2, де р – кількість вершин.

Довжина маршруту

Важливими поняттями теорії графів є поняття маршруту і шляху, які асоціюються з послідовним переміщенням від вершини до вершини по ребрах, що сполучають їх, або дугах. Маршрут довжини визначається як послідовність ребер графа таких, що граничні вершини двох сусідніх ребер співпадають. Маршрут проходить і через всі вершини, інцидентні вхідним в нього ребрам. Замкнутий маршрут приводить в ту ж вершину, з якої він починався. Маршрут, всі ребра якого різні, називається ланцюгом, а маршрут, для якого різні всі вершини, називається простій ланцюгом. Замкнутий ланцюг називається циклом, а простий замкнутий ланцюг - простим циклом. Для маршруту з n вершинами: вершини, vn називаються зв'язаними даним маршрутом (або просто зв'язаними). Вершину називають початком, а vn - кінцем маршруту. Число n називається довжиною маршруту.

Дві вершини графа називаються зв'язними, якщо існує маршрут, що сполучає ці вершини. Граф, будь-яка пара вершин якого зв'язна, називається зв'язним графом. Очевидно, що в зв'язному графові між будь-якими двома його вершинами існує простий ланцюг, оскільки з маршруту, що зв'язує їх, завжди можна видалити циклічну ділянку, що проходить через деяку вершину більше одного разу

Шлях - це маршрут, в якому всі ребра різні. Шлях називається простим, якщо і всі вершини в нім різні.

Цикл - це замкнутий шлях. Цикл 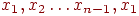називається простим, якщо всі вершини 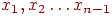попарно різні.

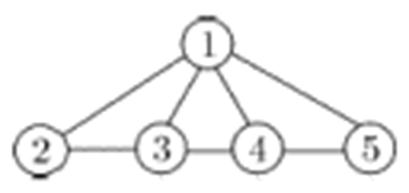
У графі на рис 3 послідовність вершин

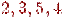· - не маршрут;

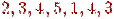· - маршрут, але не шлях;

· - шлях, але не простій;

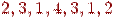· - замкнутий маршрут, але не цикл;

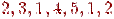· - цикл, але не простій;

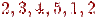· - простій цикл.

Дата добавления: 2014-01-07