Повторення дій, починаючи з п.3

Випадки:

1) Якщо отримали оптимальний план ЗЛП і в нульовому рядку останньої симплекс-таблиці вільній невідомій рівний нулю, то це свідчить про те, що існує неєдиний розв’язок задачі.

2) Якщо при переході від однієї симплекс-таблиці до іншої в ключовому стовпчику немає додатних чисел, тобто не можна жодну з базисних невідомих вивести з базису, то це означає, що цільова функція задачі лінійного програмування необмежена і оптимальних розв’язків не існує.

Приклад 2. Для виготовлення двох видів продукції П1 та П2 використовуються три види сировини S 1, S 2 та S 3. Запаси сировини, норми витрат сировини на виготовлення одиниці продукції кожного виду та дохід від одиниці продукції кожного виду наведені в таблиці:

Вид сировини	Запаси сировини	Витрати сировини на виготовлення одиниці продукції
S 1
S 2
S 3
Дохід від одиниці продукції

Необхідно знайти такий план виробництва, який забезпечить найбільший сумарний дохід.

Розв’язання:

Побудуємо математичну модель задачі.

Нехай x 1 та х 2 – загальна кількість відповідно продукції П1 та П2;

Z – сумарний дохід, який отримаємо від реалізації виробленої продукції.

Тоді математична модель задачі матиме вигляд:

,

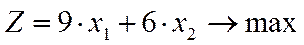за умов

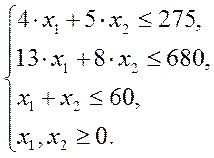
Приведемо задачу до канонічного виду:

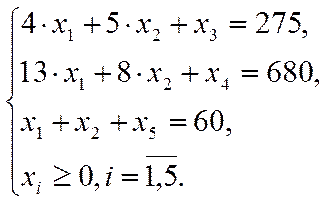
Заповнимо початкову таблицю:

№ таблиці	№ рядка	Базис	Опорний план	Коефіцієнти при невідомих
х 1	х 2	х 3	х 4	х 5
		Z
	х 3
	х 4
	х 5

№ таблиці	№ рядка	Базис	Опорний план	Коефіцієнти при невідомих
х 1	х 2	х 3	х 4	х 5
		Z
	х 3
	х 4
	х 5

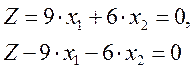
Отримали:

№ таблиці	№ рядка	Базис	Опорний план	Коефіцієнти при невідомих
х 1	х 2	х 3	х 4	х 5
		Z		-9	-6
	х 3
	х 4
	х 5

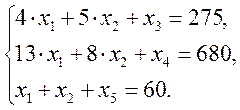
№ таблиці	№ рядка	Базис	Опорний план	Коефіцієнти при невідомих
х 1	х 2	х 3	х 4	х 5
		Z		-9	-6
	х 3
	х 4
	х 5

Отже, початковий опорний план:

х_опорн.= (0; 0; 275; 680; 60).

ЦФ: Z (х_опорн.) = 9·0+6·0=0.

- в нульовому рядку є два від’ємних числа ((-9) та (-6)), значить досліджуваний опорний план не є оптимальним.

№ таблиці	№ рядка	Базис	Опорний план	Коефіцієнти при невідомих
х 1	х 2	х 3	х 4	х 5
		Z		-9	-6
	х 3
	х 4
	х 5

№ таблиці	№ рядка	Базис	Опорний план	Коефіцієнти при невідомих
х 1↓	х 2	х 3	х 4	х 5
		Z		-9	-6
	х 3
	х 4
	х 5

- визначимо, яку з невідомих потрібно вивести з базису:

№ таблиці	№ рядка	Базис	Опорний план	Коефіцієнти при невідомих
х 1↓	х 2	х 3	х 4	х 5
		Z		-9	-6
	х 3
	х 4 ←
	х 5

275: 4 = 68,75;

680:13 = 52,3; (min) – ключовим

60:l=60.

№ таблиці	№ рядка	Базис	Опорний план	Коефіцієнти при невідомих
х 1↓	х 2	х 3	х 4	х 5
		Z		-9	-6
	х 3
	х 4 ←
	х 5

Переходимо до другої симплекс-таблиці.

Замість невідомої х 4 в базис вводимо невідому x 1.

№ таблиці	№ рядка	Базис	Опорний план	Коефіцієнти при невідомих
х 1	х 2	х 3	х 4	х 5
		Z		-9	-6
	х 3
	х 1	680/13	13/13	8/13		1/13
	х 5

№ таблиці	№ рядка	Базис	Опорний план	Коефіцієнти при невідомих
х 1	х 2	х 3	х 4	х 5
		Z		-9	-6
	х 3
	х 1	680/13		8/13		1/13		(9)
	х 5

№ табл.	№ рядка	Б	ОП	Коефіцієнти при невідомих
х 1	х 2	х 3	х 4	х 5
		Z	0+9*680/13= =6120/13	-9+9=0	-6 + 72/13= =(-78+72)/13= =- 6/13		9/13
	х 3
	х 1	680/13		8/13		1/13		(-4)
	х 5

№ табл.	№ рядка	Б	ОП	Коефіцієнти при невідомих
х 1	х 2	х 3	х 4	х 5
		Z	6120/13		–6/13		9/13
	х 3	855/13		5 – 32/13=33/13		-4/13
	х 1	680/13		8/13		1/13
	х 5

№ табл.	№ рядка	Б	ОП	Коефіцієнти при невідомих
х 1	х 2	х 3	х 4	х 5
		Z	6120/13		–6/13		9/13
	х 3	855/13		33/13		-4/13
	х 1	680/13		8/13		1/13		(-1)
	х 5

№ табл.	№ рядка	Б	ОП	Коефіцієнти при невідомих
х 1	х 2	х 3	х 4	х 5
		Z	6120/13		–6/13		9/13
	х 3	855/13		33/13		-4/13
	х 1	680/13		8/13		1/13
	х 5	100/13		5/13		-1/13

Новий опорний план:

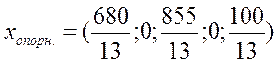
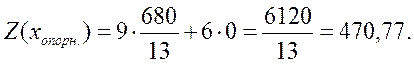
Але, в нульовому рядку є ще від’ємне число (), значить вищезгаданий опорний план не є оптимальним.

- невідому (x 2) вводимо в базис:

№ табл.	№ рядка	Б	ОП	Коефіцієнти при невідомих
х 1	х 2 ↓	х 3	х 4	х 5
		Z	6120/13		–6/13		9/13
	х 3	855/13		33/13		-4/13
	х 1	680/13		8/13		1/13
	х 5 ←	100/13		5/13		-1/13

855/13: 33/13 = 25,9;

680/13: 8/13 = 85;

100/13: 5/13 = 20 (min).

Отже, замість невідомої х 5 в базис вводимо невідому х 2.

№ табл.	№ рядка	Б	ОП	Коефіцієнти при невідомих
х 1	х 2 ↓	х 3	х 4	х 5
		Z	6120/13		–6/13		9/13
	х 3	855/13		33/13		-4/13
	х 1	680/13		8/13		1/13
	х2	100/13		5/13		-1/13		:5/13

№ табл.	№ рядка	Б	ОП	Коефіцієнти при невідомих
х 1	х 2 ↓	х 3	х 4	х 5
		Z	6120/13		–6/13		9/13
	х 3	855/13		33/13		-4/13
	х 1	680/13		8/13		1/13
	х2					-1/5	13/5	6/13

№ табл.	№ рядка	Б	ОП	Коефіцієнти при невідомих
х 1	х 2 ↓	х 3	х 4	х 5
		Z					3/5	6/5
	х 3	855/13		33/13		-4/13
	х 1	680/13		8/13		1/13
	х2					-1/5	13/5	-33/13

№ табл.	№ рядка	Б	ОП	Коефіцієнти при невідомих
х 1	х 2 ↓	х 3	х 4	х 5
		Z					3/5	6/5
	х 3					1/5	-33/5
	х 1	680/13		8/13		1/13
	х2					-1/5	13/5	(-8/13)

№ табл.	№ рядка	Б	ОП	Коефіцієнти при невідомих
х 1	х 2 ↓	х 3	х 4	х 5
		Z					3/5	6/5
	х 3					1/5	-33/5
	х 1					1/5	-8/5
	х2					-1/5	13/5

Отже, нульовому рядку останньої таблиці немає від’ємних чисел, тому оптимальний розв’язок:

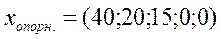
Невідомі х 4=0 та х 5=0, а це означає, що сировина S 2 та S 3 використана повністю, х 3=l5, значить сировина S 1 є в залишку (недовикористана) 15 одиниць.

Дата добавления: 2014-01-07