Статистическая обработка результатов моделирования

Оцінювання кореляційного моменту

Для обчислення оцінки кореляційного моменту можна використовувати формулу

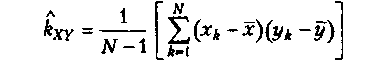
або, більш зручну для обчислень,

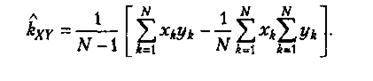
При обчисленнях за цією формулою теж доцільно змінити послідовність дій.

В ходе статистического моделирования формируются выборочные данные, описывающие процесс и результаты функционирования системы. Выборочные данные являются исходным статистическим материалом для нахождения приближенных значений (оценок) показателей эффективности функционирования изучаемой системы.

Оцінка статистичних характеристик. За результатами імітаційного моделювання розраховують наступні основні статистичні характеристики показників ефективності системи:

оцінка математичного очікування (вибіркове середнє);

вибіркова медіана;

вибіркова мода;

оцінка дисперсії;

оцінка среднеквадратического відхилення;

вибіркові мінімальне і максимальне значення;

вибірковий розмах;

коефіцієнт варіації.

Оценка статистических характеристик. По результатам имитационного моделирования рассчитывают следующие основные статистические характеристики показателей эффективности системы:

оценка математического ожидания (выборочное среднее);

выборочная медиана;

выборочная мода;

оценка дисперсии;

оценка среднеквадратического отклонения;

выборочные минимальное и максимальное значения;

выборочный размах;

коэффициент вариации.

Нехай -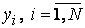 вибіркові дані (спостереження), отримані в результаті проведення 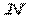експериментів з імітаційною моделлю системи.

Наприклад, в якості 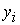можуть виступати: час перебування заявки в системі; час знаходження заявки в черзі на обслуговування; час обробки заявки і ряд інших характеристик.

В термінах математичної статистики показник 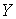- випадкова величина, а 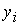- вибіркові значення ВВ, отримані в результаті спостережень (вимірів) ВВ.

Теоретичне математичне очікування неперервної ВВ Y, можливі значення якої належать усій числовій осі, визначається по формулі:

,

(3.26)

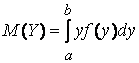
де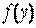- функція щільності розподілу імовірності ВВ.

Якщо можливі значення ВВ належать інтервалу (a, b), то теоретичне математичне очікування знаходиться по формулі:

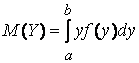(3.27)

Математичне очікування - це, мабуть, основна і найбільш вживана характеристика центру групування ВВ.

Оцінку математичного очікування (вибіркове середнє) отримують як середнє арифметичне значення :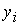

.

(3.28)

Медіана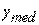 визначається як середньоімовірністне значення ВВ, тобто імовірність того, що аналізована ВВ виявиться більше медіани, дорівнює імовірності того, що аналізована ВВ виявиться менше медіани і рівна 0.5. Медіана також як і математичне очікування відноситься до характеристик групування.

Вибірковий аналог медіани 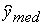визначається як середнє (по місцю розташування) значення ранжируваного (варіаційного), тобто розташованого в порядку зростання ряду спостережень.

Якщо кількість спостережень N непарно, то

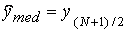, (3.29)

якщо N парно, то

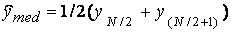. (3.30)

Вибіркова мода 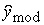є найбільш значенням, що часто зустрічається у вибіркових спостереженнях, тобто значення яке є "модним". Мода відноситься до характеристик центру групування.

Теоретична дисперсія неперервної ВВ Y, можливі значення якої належать інтервалу (a, b), обчислюється за формулою:

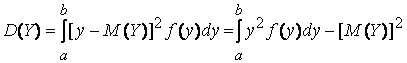. (3.31)

Оцінку дисперсії можна знайти по формулі:

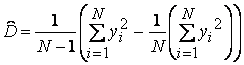(3.32)

Дисперсія відноситься до характеристик міри розсіяння значень досліджуваною ВВ відносно центру групування. Значення дисперсії дає уявлення про те, як сильно можуть відхилятися від середнього значення вибіркові дослідження

Вибіркове середньоквадратичне відхилення (СКО):

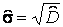(3.33)

СКВ використовується разом з вибірковою дисперсією для характеристики міри відхилення спостережуваних значень від середнього значення і виявляється у ряді випадків зручнішим і природнішим, оскільки СКВ має ту ж розмірність, що і аналізований показник і відповідно вибіркові середнє, медіана, мода.

Ще одна характеристика розкиду (розсіяння) цих спостережень - вибірковий розмах:

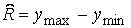(3.34)

де - максимальне вибіркове значення;

- мінімальне вибіркове значення.

Вибірковий коефіцієнт варіації використовується в тих випадках, коли міру розсіяння природно описувати деякою відносною характеристикою відповідно до середнього:

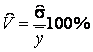(3.35)

Вибірковий коефіцієнт варіації вимірюється у відсотках. За значенням коефіцієнта варіації можна висунути гіпотезу про тип закону розподілу ВВ Y.

Наприклад, для експоненціального розподілу =100%; для гамма розподілу і розподілу Вейбулла може бути <100%, =100%, >100%, коли параметр форми розподілів відповідно до <1, =1, >1.

Приклад. Обчислювальна система складається з двох комп'ютерів, інтервали часу між двома послідовними вступами завдань підкоряються рівномірному закону розподілу в інтервалі (10,16). Перед кожним комп'ютером допустима черга завдань, довжина якої не обмежена. Час виконання завдань також рівномірно розподілений в інтервалі (20,30).

В результаті імітаційного моделювання обчислювальної системи засобами GPSS отримані вибіркові дані часу перебування завдань в системі за результатами 100 експериментів (приведена частина даних):

17,272; 22,138; 22,516; 23,741; 21,409; 24,217; 24,306; 23,724, 24,974; 24,507; 23,251; 25,086; 25,416; 25,276; 24,993; 25,888; 26,204; 26,296; 25,549.

Необхідно розрахувати статистичні характеристики Необхідно розрахувати статистичні характеристики показника "час перебування завдання в системі" і зробити висновки про ефективність функціонування системи за цим критерієм.

Отримані наступні результати.

Середній час перебування завдання в системі складає: 26,18 секунд.

Середньоімовірностний час знаходження завдання в системі дорівнює 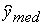=26,67 секунд. Іншими словами 50% завдань знаходяться в обчислювальній системі менше 26,67 секунд і 50% більше цього часу.

Для даних прикладу мода множинна, у вибіркових даних немає значень що повторюються, оскільки точність обчислення три знаки після коми. Проте, можна сказати, що найбільш імовірний час перебування завдання в системі лежить в інтервалі (26; 27), в цей інтервал потрапляють 73 вибіркові спостереження з 100.

Вибіркова дисперсія приблизно дорівнює 1,99. Міра відхилення часу знаходження завдання в системі від середнього значення (26,18 сек.) складає 1,99 сек.².

Середньоквадратичне відхилення приблизно складає 1,4 секунд. Міра відхилення часу перебування завдання в системі від середнього часу (26,18 секунд) складає 1,4 секунд.

Мінімальний час перебування завдання в обчислювальній системі: 17,27 сек. за результатами 100 експериментів; максимальний час перебування завдання в системі: 27,2 сек. Для даних прикладу розмах складає 9,93 секунд. Отже, різниця між мінімальним і максимальним часом знаходження завдання в системі складає 9,93 секунд.

Аналіз статистичних характеристик показника "час перебування завдання в системі" дозволяє зробити наступні висновки про ефективність функціонування обчислювальної системи:

· середній час перебування завдання в системі 26,18 сек. порівнянно з часом обробки завдання комп'ютером (20-30 секунд), отже, час очікування завдання в черзі на обробку – незначний.

· розкид часу перебування завдання в системі відносно середнього також не значний: СКВ складає 1,4 секунд; 73 значення з 100 потрапляють у вузький інтервал (26-27 секунд).

Таким чином, за критерієм "час знаходження завдання в системі" обчислювальна система функціонує ефективно

Визначення об'єму вибірки. Об'єм вибірки - це кількість реалізацій, яка потрібна при імітаційному моделюванні, щоб забезпечити стохастичну точність результату.

При обчисленні оцінки математичного очікування із заданою точністю і достовірністю об'єм вибірки можна вичислити по формулі:

, (3.36)

де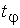 - квантиль нормального розподілу рівня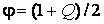; - рівень довірчої імовірності; 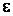- точність оцінки математичного очікування.

Кількість реалізацій для отримання оцінки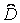 із заданою точністю 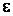обчислюється за формулою:

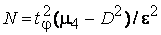(3.37)

де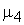 - центральний момент четвертого порядку ВВ.

Для практичного використання формул (3.36, 3.37) необхідно знати теоретичн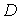і і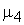, які, як правило, бувають невідомими. В цьому випадку використовують оцінки 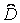і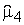, отримувані заздалегідь, при деякому N. Якщо при цьому задана точність 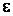не досягнута, то N збільшують, після чого проводиться уточнення оцінок. Цей процес повторюється до тих пір, поки не буде забезпечена задана точність.

Перевірка гіпотези про тип закону розподілу ВВ.

При обробці результатів машинного експерименту з моделлю системи часто виникає завдання визначення емпіричного закону розподілу ВВ. Для цього будують гістограму (емпіричну оцінку функції щільності розподілу імовірності ВВ, і на основі її аналізу висувають гіпотезу про тип закону розподілу ВВ. Перевірка гіпотези реалізується за допомогою критеріїв згоди (Колмогорова - Смирнова, Пірсону, Крамера - Мизеса - Смирнова і інших).

Загальна схема рішення цієї задачі зводиться до наступного:

· будують по результатам імітаційного експерименту гістограму;

· висувають гіпотезу про згоду емпіричного закону з будь-яким теоретичним розподілом;

· перевіряють гіпотезу з допомогою одного з статистичних критеріїв згоди (хі-квадрат Персона, Колмогорова –Смірнова та інших)

Для побудови гістограми інтервал виміру ВВ розбивають на рівні відрізки завдовжки, кожному з них зіставляють лічильник, де накопичують 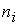- кількість попадань значень ВВ в i -й відрізок. На кожному відрізку будується прямокутник з висотою 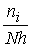. На отриману гістограму накладають неперервну криву функції щільності передбачуваного теоретичного розподілу.

Критерій згоди Пірсона. В якості критичної статистики в критерії згоди Пірсона використовують величину, яка характеризує міру розбіжності емпіричного і теоретичного закону розподілу:

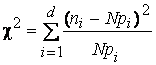(3.38)

де 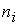- кількість значень ВВ, що потрапили в i - ий інтервал;

- теоретична вірогідність попадання ВВ в i - ий інтервал;

d - кількість інтервалів групування;

N - об'єм спостережень.

Критична статистика розподілена за законом хі квадрат

із 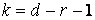ступенями свободи, де 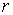- число параметрів теоретичного закону розподілу.

Перевірка гіпотези про згоду емпіричного і теоретичного законів розподілу за допомогою критерію згоди Пірсона здійснюється в наступній послідовності.

· Результати спостережень групують в інтервальний варіаційний ряд. Об'єм спостережень має бути досить великим (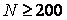). Якщо частота, що відповідає якому-небудь інтервалу, виявиться менше 5, то інтервал об'єднують з сусіднім.

· Висувають гіпотезу про вид розподілу ВВ на основі візуального аналізу гістограми. Задають рівень значущості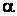

· Визначають теоретичну імовірність 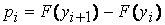попадання ВВ в кожний з інтервалів.

· Обчислюють критичну статистику

· Знаходять нижню і верхню критичні межі по таблиці розподілу (квантилі відповідно рівнів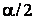 і):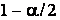

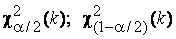
· Перевіряють виконання нерівності: 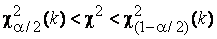. Якщо нерівність виконується, то гіпотеза про згоду теоретичного і емпіричного розподілів ВВ не відкидається при рівні значущості .

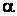Дата добавления: 2014-01-07