Характеристики случайных сигналов

Случайной называется функция некоторой независимой переменной, значение которой при каждом данном значении независимой переменной является случайной величиной. Если независимая переменная - время, то случайная функция называется случайным (стохастическим или вероятностным) процессом.

Случайный процесс, в отличие от детерминированного, нельзя описать какой-либо определенной функцией времени 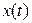. Случайный процесс представляет собой множество функций 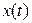, обладающие некоторыми общими вероятностными свойствами.

Реализацией случайного процесса называется конкретная функция 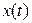, которая получена в результате экспериментального наблюдения. Случайные процессы подразделяются на стационарные и нестационарные.

Стационарный случайный процесс - это процесс, статистические характеристики которого не изменяются во времени.

Нестационарный случайный процесс имеет статистические характеристики, которые с течением времени меняются.

Реальные системы, как правило, характеризуются стационарным случайным процессом.

Математический аппарат анализа стационарных случайных процессов основан на гипотезе эргодичности. Согласно гипотезе эргодичности статистические характеристики большого числа произвольно выбранных реализаций случайного стационарного процесса совпадают со статистическими характеристиками одной реализации достаточно большой длины. Это означает, что усреднение по множеству реализаций стационарного случайного процесса можно заменить усреднением по времени одной достаточно большой реализации. Тем самым существенно облегчается экспериментальное определение статистических характеристик стационарного случайного процесса и упрощается расчет систем при случайных воздействиях.

Дата добавления: 2014-01-07