
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция n8
|
|
|
|
.
Допустим, что годовой модуль стока реки аналога в 1919 г.
Ма=10.0 л/ (с км2). Из уравнения (11) находим годовой модуль стока в изучаемом бассейне в 1919 г.
М1919= 10.72+0.98  л/(с км2)
л/(с км2)
в 1920 г. Ма = 6.8 л/(с км2), тогда
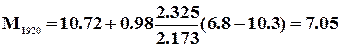 л/ (с км2)
л/ (с км2)
Аналогично определяем значение годового стока изучаемого бассейна для всех последующих лет за которые имеются наблюдения в аналоге.
По удлиненному ряду находим норму стока, как среднее арифметическое

| 1(12) |
3. Определение нормы стока по графику связи. Исходные данные: годовые модули стока в изучаемом бассейне за период n=10 лет.
В данной работе бассейн-аналог указан и приведены данные наблюдений в нем за многолетний период (n=25 лет).
Данные одновременных наблюдений (за период n лет) наносятся на координатную сетку, откладывая по оси ординат годовые модули стока в изучаемом бассейне (М), по оси абсцисс - модули стока в бассейне- аналоге (Ма). По этим точкам проводим линию связи таким образом, чтобы она удовлетворяла равномерному расположению точек по обе стороны. Масштаб построения графика связи выбирают так, чтобы линия связи проходила примерно под углом 450.Для построения удовлетворительной прямолинейной связи годовых значений стока необходимо иметь одновременные наблюдения в изучаемом и аналогичном бассейне не менее 6 лет (n ³ 6 лет). Отклонение большей части точек от линии связи не должно превышать 15%.
Вычислив норму стока в бассейне аналоге непосредственно по длинному ряду наблюдений (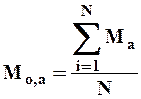 ), откладываем ее значения на оси абсцисс и по графику связи находим норму стока в изучаемом бассейне.
), откладываем ее значения на оси абсцисс и по графику связи находим норму стока в изучаемом бассейне.
На рис. 1 приведен график связи между годовыми модулями стока р.Камы у пр. Дворянской и р. Камы у г. Перми за 1909 - 1918 гг. По норме стока аналога Мо,а=10.26 л/(с км2) графически определяем соответствующее ей значение нормы в расчетном створе (р.Кама у пр. Дворянская) Мо=10.7 л/(с.км2).
 Mn,a
Mn,a
Рис.1. График связи между годовыми модулями стока р. Камы у пр. Добрянская (М) и р. Камы у г. Пермь (М0).
3. Определение нормы стока по приближенной формуле. Норму стока по приближенной формуле определяют при очень коротком периоде наблюдений (n< 6 лет). Этот способ исходит из предположения, что линия связи стока в двух бассейнах проходит через начало координат и соотношение стока за различные периоды остается постоянным, а именно
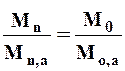
| (13) |
где Мn , Mn,a - среднее значение стока в изучаемом и аналогичном бассейне за одновременный короткий период наблюдений;
Мо, Мо,а - норма стока в изучаемом и аналогичном бассейне. Отсюда норма стока в изучаемом бассейне (с коротким периодом наблюдений) равна
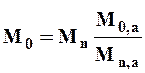
| (14) |
Формула (14) может быть использована в случае, когда отношение  находится в пределах 0.8-1.4, а отношение коэффициентов вариации стока в изучаемом и аналогичном бассейне
находится в пределах 0.8-1.4, а отношение коэффициентов вариации стока в изучаемом и аналогичном бассейне 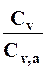 в пределах 0.8 - 1.2. Расчет по формуле (14) производим по тем же исходным данным, что и в предыдущем параграфе.
в пределах 0.8 - 1.2. Расчет по формуле (14) производим по тем же исходным данным, что и в предыдущем параграфе.
4. Определение нормы стока при отсутствии гидрометрических данных. При отсутствии наблюдений над стоком норму стока для какой-либо неизученной реки можно приближенно определить по картам изолиний среднего годового стока. Такая карта для всего Советского Союза составлена в 1946 г. Б.Д. Зайковым.
В 1962 г. опубликована уточненная карта К.П. Воскресенским по большому количеству пунктов наблюдений и по более длинным рядам стока.
Как это было показано на рис.2, для определения нормы стока какой-либо неизученной реки на карте изолиний стока проводится водораздельная линия бассейна реки до замыкающего створа А и определяется М - центр тяжести бассейна; значение модуля стока для центра тяжести М определяется путем интерполяциии между соседними изолиниями, в рассматриваемом примере - между изо-линиями 5 и 6 л/сек с 1 км2, и получается равным 5.3 л/(с км2). Это значение и принимается в качестве нормы стока для бассейна реки до замыкающего створа А.
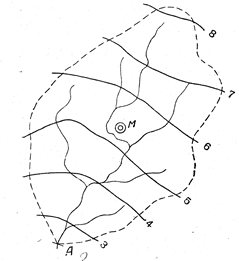
Рис.2. Определение среднего многолетнего стока по карте изолиний модулей стока (л/сек с 1 км2).
Определив норму стока в виде модуля, можно вычислить значение среднего годового многолетнего расхода по формуле
 м3/сек, м3/сек,
| (15) |
где М0 - модуль стока, определенный по карте для центра тяжести бассейна, в л /сек с км2; F - площадь бассейна до данного замыкающего створа в км2.
Для очень больших речных водосборов и при различии в нормах стока на отдельных составляющих водосбора следует определять по карте изолиний средневзвешенный модуль стока по следующей формуле
 л /сек с км2 л /сек с км2
| (16) |
где М1, М2,..., Мn - средние арифметические значения модулей стока соседних изолиний, ограничивающих отдельные бассейна, f1, f2,..., fn - площади бассена между соседними изолиниями стока, определяемые планиметрированием.
Определение нормы стока по картам изолиний на Европейской территории России для больших бассейнов может быть сделано с точностью до 3-5 %; для малых бассейнов точность определения нормы стока рек значительно снижается.
Распределение нормы стока рек по территории РФ имеет ясно выраженную широтную зональность.
В заключении первой части настоящей расчетно-графической работы следует произвести сопоставление результатов расчета нормы годового стока различными способами, принимая в качестве основного способа - определение нормы стока по многолетним гидрометрическим данным.
Для рассмотренного примера результаты расчета нормы годового стока приведены в таблице 4.
Таблица 4
| Много-летний ряд | Метод корреляции --------------------------- | График связи | Приближенная формула | Карта изолиний | ||
| Уравнение регоессии | Удлиненныйряд | |||||
| М л/с.км2 | ||||||
| % отклоне-ния | - |
Содержание: Изменчивость характеристики стока. Кривые распределения и кривые обеспеченности стока. Параметры кривых. Применение эмпирических и аналитических кривых (трехпараметрического гамма распределения и биноминальной кривой) к расчетам стока.
1.Изменчивость характеристики стока. Величины годового стока непрерывно колеблются под влиянием климатических (осадков и испарения) и физико-географических факторов. Длительными наблюдениями установлено, что колебания годового стока носят циклический характер, выражающийся в последовательной смене многоводных и маловодных лет. Установлено, что появление в том или ином календарном году того или иного годового стока из числа возможных является случайным. Также являются случайными календарные последовательности значений годового стока. Кроме того, как показали исследования, между величинами стока за смежные годы имеется лишь незначительная корреляционная связь, что дает возможность в большинстве случаев пренебрегать ею. Следовательно величины годового стока являются случайными, а ряд образованный ими, вариационным рядом.
При определении расчетных гидрологических характеристик, широко применяются различные теоретические функции распределения. Среди многочисленных кривых распределения наибольший практический интерес представляют функции гамма распределения, распределение Пирсона III типа и трехпараметрическое гамма-распределение С.Н. Крицкого и М.Ф. Менкеля (1946 г.).
Гамма распределение занимает особое положение при описании существенно положительных случайных величин, варьирующих в интервале
¥ >Х >0. Величины речного стока не могут принимать значений меньше нуля, поэтому гамма распределение широко применяется в гидрологии.
С помощью гаммак распределения удовлетворительно описываются колебания величин годового стока, максимальных расходов воды весеннего половодья и других гидрологических характеристик.\В гидрологии гамма-распределение иногда называют кривой биноминального типа и совпадают с типом III кривых Пирсона.
Уравнение плотности вероятностей гамма-распределения имеет вид:
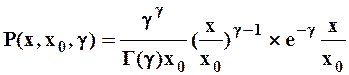
| ((1) |
где Х0 - центр (среднее) распределения; g - параметр, связанный с коэффициентом изменчивости простым соотношением:
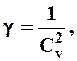
| ((2) |
Г(g) - cимвол гамма-функции (интеграла Эйлера II рода);
Г(g)
| ((3) |
Гамма распределение содержит два параметра, характеризующих центр распределения и его рассеяние. Это распределение имеет положительную асимметрию, коэффициент асимметрии Сs функциональной связи с коэффициентом изменчивости Сv соотношением Сs = 2 Сv.
Распределение Пирсона III типа. Распределение вероятностей многих гидрологических величин (ливневые осадки, максимумы дождевых паводков в малых реках и т.п.) характеризуются значительной асимметрией, иногда в несколько раз превышающий асимметрию гамма-распределения. В связи с этим возникает необходимость в более гибком - трехпараметрическом распределении вероятностей. До сравнительно недавнего времени в качестве такого распределения применялись почти исключительно кривые Пирсона III типа.
Уравнение плотности вероятностей этих кривых имеет вид
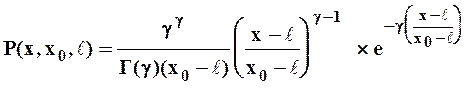 при х> при х> 
| (4) |
где x0 - среднее распределение; 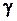 и
и  - параметры распределения.
- параметры распределения.
Связь между этими и стандартными параметрами 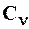 и
и  выражается соотношениями:
выражается соотношениями:
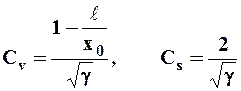
| (5) |
Cемейство кривых распределения Пирсона III типа допускает свободный выбор трех параметров: среднего x0, коэффициента изменчивости 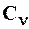 и коэффициента асимметрии
и коэффициента асимметрии  .
.
Распределение Пирсона является линейным преобразованием гамма распределения: она получается "сдвигом" гамма распределения по оси абсцисс на величину  . Для различных значений
. Для различных значений  , мы будем получать распределения с различной относительной асимметрией
, мы будем получать распределения с различной относительной асимметрией  /
/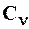 . Величины
. Величины  , т.е. начало кривой, связаны с
, т.е. начало кривой, связаны с 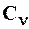 и
и  равенством:
равенством:
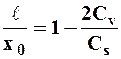
| (6) |
Таким образом, как видно из уравнений (6) распределение Пирсона III типа ограничено снизу величиной  , которая определяет асимметрию распределения. Последнее формально следует из уравнений кривой Пирсона III типа и никак не определяется природой явления речного стока. Это является принципиальным недостатком кривых Пирсона III типа. Кроме того, как видно из рис.2, следует, что
, которая определяет асимметрию распределения. Последнее формально следует из уравнений кривой Пирсона III типа и никак не определяется природой явления речного стока. Это является принципиальным недостатком кривых Пирсона III типа. Кроме того, как видно из рис.2, следует, что

| (7) |
C другой стороны, при интегрировании биномиальной кривой распределения получено:
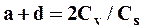
| (8) |
Cоответственно, из (15), (16) получаем:
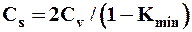
| (9) |
Анализ (17) показывает:
если  = 2
= 2 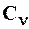 , то Кmin= 0 и, следовательно, кривая выходит из начала координат;
, то Кmin= 0 и, следовательно, кривая выходит из начала координат;
при  > 2
> 2 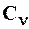 , то Кmin> 0 и начало кривой отстоит вправо от начала координат на величину Кmin;
, то Кmin> 0 и начало кривой отстоит вправо от начала координат на величину Кmin;
если же  < 2
< 2 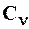 , то Кmin< 0, т.е. имеет отрицательное значение, что противоречит физической сущности гидрологической характеристики.
, то Кmin< 0, т.е. имеет отрицательное значение, что противоречит физической сущности гидрологической характеристики.
Отмеченный недостаток кривых Пирсона III типа побудил к поиску других схем, которые позволили бы свободно выбирать третий параметр, не связывая его с началом кривых.
Одной из таких схем является, так называемое трехпараметрическое гамма-распределение. Основное его преимущество заключается в том, что при любых соотношениях между коэффициентом изменчивости 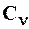 и коэффициентом асимметрии
и коэффициентом асимметрии  нижним пределом варьируемого признака будет нуль.
нижним пределом варьируемого признака будет нуль.
Уравнение плотности вероятностей трехпараметрического распределения С.Н.Крицкого и М.Ф.Менкеля имеет вид:
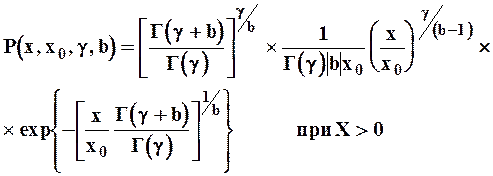 
| (10) |
В этом уравнении x0 -среднее распределение; 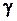 и b - параметры распределения, каждому сочетанию которых соответствуют определенные значения коэффициентов изменчивости
и b - параметры распределения, каждому сочетанию которых соответствуют определенные значения коэффициентов изменчивости 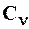 и коэффициентом асимметрии
и коэффициентом асимметрии  . Связь между параметрами распределения
. Связь между параметрами распределения 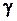 и b и стандартными параметрами
и b и стандартными параметрами 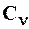 и
и  выражается следующими трансцендентными уравнениями:
выражается следующими трансцендентными уравнениями:
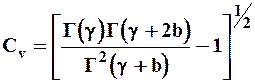
| (11) |
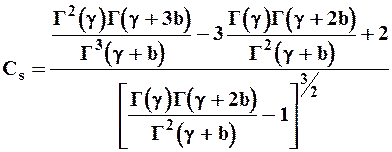
| (12) |
Для определения параметров кривых распределения используются три способа: метод наибольшого правдоподобия, метод моментов или графоаналитический метод.
Метод наибольшого правдоподобия предложен английским математиком Р.Фишером. Он заключается в том, что параметры распределения подбирают по принципу наибольшого правдоподобия, т.е. принимают такие значения, при которых результаты наблюдений имеют наибольшую вероятность совместного появления, или, другими словами, наиболее правдоподобны.
Аналитическое решение этой задачи, данное С.Н.Крицким и М.Ф. Менкелем, требует громоздких вычислений. Поэтому с целью облегчения практического применения этого метода для трехпараметрического гамма-распределения Е.Г.Блохинов построил номограммы, которые позволяют определять расчетные значения коэффициента вариации Сv и коэффициента асимметрии Cs в зависимости от статистик  и
и 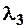 , вычисляемых по формулам:
, вычисляемых по формулам:

| (13) |
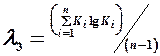
| (14) |
где Ki - модульный коэффициент рассматриваемой гидрологической характеристики; n - число членов рядов.
Метод моментов заключается в том, что параметры кривой обеспеченности (и распределения) устанавливают на основе понятия о моментах статистических совокупностей. По аналогии с механикой под моментами статистических совокупностей понимают произведения случайной величины x или ординаты кривой распределения на расстояние до выбранной точки. В математической статистике наиболее часто используют моменты двух видов; начальные - относительно начала координат и центральные - относительно среднего арифметического.
Начальный момент порядка m случайной величины x представляют собой выражение вида

| (17) |
В частном случае при m=1 начальный момент, называемый первым, соответствует среднеарифметическому значению рассматриваемой переменной, т.е.
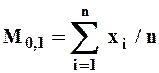
| (18) |
Это одна из формул метода моментов, позволяющая определить один из основных параметров аналитической кривой обеспеченности - норму стока.
Центральным моментом порядка m случайной величины x называют среднее значение отклонений x от ее среднеарифметического значения в степени m:

| (19) |
Второй центральный момент (при m=2)

| (20) |
Если сопоставить это выражение с формулой
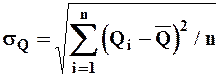
| (21) |
то окажется, что
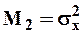
| (22) |
т.е. равен среднеквадратическому отклонению во второй степени (дисперсии). Откуда следует, что

| (23) |
а коэффициент вариации
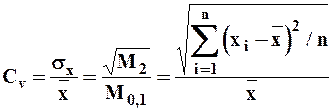 , ,
| (24) |
или в безразмерном виде

| (25) |
Третий центральный момент

| (26) |
Откуда следует, что коэффициент асимметрии

| (27) |
а для ряда модульных коэффициентов
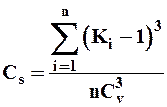
| (28) |
При наличии ограниченных выборок, второй центральный момент (22) имеет отрицательное смещение (систематическое занижение). Для его устранения в (22) вводится поправка  , c учетом этого получаем общее выражение
, c учетом этого получаем общее выражение
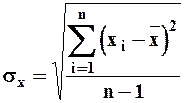
| (29) |
Соответственно этому и коэффициент вариации (24) примет следующий окончательный вид:

| (30) |
Как  и
и 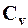 , параметр
, параметр  также является смешанной оценкой. Для устранения вводится поправка
также является смешанной оценкой. Для устранения вводится поправка  , тогда
, тогда

| ((31) |
Графо-аналитический метод Г..А. Алексеева. Для определения параметров кривой обеспеченности, т.е. Q0, Cv, и Cs Г.А. Алексеева выполняем следуюшие процедуры:
1. Имеющийся ряд годовых расходов (объемов) Q1, Q2,,QN располагаем в убывающем порядке и получаем ранжированный ряд годовых расходов воды.
2. Используя формулы 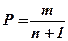 определяем величину обеспеченности для каждого члена ряда.
определяем величину обеспеченности для каждого члена ряда.
3. По парным значениям (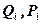 ) на клетчатке вероятностей строим сглаженную (осредненную) эмприческую кривую обеспеченности
) на клетчатке вероятностей строим сглаженную (осредненную) эмприческую кривую обеспеченности 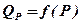 .
.
4. На кривой 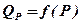 выбираем три опорные точки, соответствующие
выбираем три опорные точки, соответствующие  обеспеченности:
обеспеченности:  т. е.
т. е. 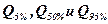 .
.
Вычисляем коэффициент скошенности
 (1)
(1)
6. По значению  из пролежения 4 в книге «Практикум по инженерной гидрологии и регулированию стока. М: Колос, 1996. С.209-210» определяем параметры СS, Ф5%-Ф95%, Ф50%.
из пролежения 4 в книге «Практикум по инженерной гидрологии и регулированию стока. М: Колос, 1996. С.209-210» определяем параметры СS, Ф5%-Ф95%, Ф50%.
7. Определяем значения параметров кривой обеспеченности
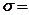
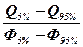 (2)
(2)
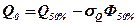 (3)
(3)
 (4)
(4)
В инженерной гидрологии для изучения колебаний годового стока и оценки изменений его характеристики в будущем широко используются кривые обеспеченности стока.
Кривые обеспеченности стока. Обеспеченностью заданного значения гидрологических характеристик называется вероятность ежегодного его превышения.
Обеспеченностью годового стока может быть названо среднее число лет (выраженное в процентах или долях от общего числа лет), в котором годовой сток будет равен или больше данного.
Кривая обеспеченности (или кривая превышения) - это интегральная кривая, показывающая обеспеченность или вероятность превышения (в процентах или в долях от единицы) данной величины среди общей совокупности ряда. Следовательно, если обеспеченность годового стока Qi (или Wi) равна Р%, это означает, что число членов в данном ряду, больших или равных Qi, составляет Р% от общего числа членов ряда.
Рассмотрим как можно построить кривую повторяемости (частоты) и эмпирическую кривую обеспеченности среднегодовых величин стока.
Пусть имеются данные наблюдений за годовым стоком за период n лет: Q1,Q2,...,Qi,..., Q n (где Qi - средний годовой сток в i-м году). Выразим эти данные в относительных величинах (модульные характеристики стока): 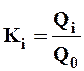 где Q0 - среднее арифметическое значение ряда) и расположим их в убывающем порядке от Кmах до Кmin. Если такой ряд разбить на одинаковые интервалы DК и подсчитать абсолютную nj частоты повторений каждого интервала модульных коэффициентов Кj (
где Q0 - среднее арифметическое значение ряда) и расположим их в убывающем порядке от Кmах до Кmin. Если такой ряд разбить на одинаковые интервалы DК и подсчитать абсолютную nj частоты повторений каждого интервала модульных коэффициентов Кj ( ), то можно построить ступенчатый график распределения частоты, или вероятностей, среднегодовых расходов воды. Такой график в математической статистике называется гистограммой распределения (рис. 1).
), то можно построить ступенчатый график распределения частоты, или вероятностей, среднегодовых расходов воды. Такой график в математической статистике называется гистограммой распределения (рис. 1).
Рис. 1 Гистограмма (1) и эмпирическая кривая обеспеченности (2) среднегодовых расходов воды.
При неограниченном росте членов ряда (n ® ¥) и стремлении DК ® 0 гистограмма распределения превращается в плавную кривую, которую называют кривой распределения вероятностей (рис. 2). Кривая распределения дает наглядное представление о законе распределения случайной величины. Она характеризует вероятность появления того или иного значения рассматриваемого ряда случайных величин. Из ее рассмотрения, в частности, следует, что чем ближе значение члена ряда к среднему, тем больше вероятность его появления (частота) и, наоборот, чем больше отклонение члена ряда от среднего, тем меньше его вероятность появления.
Рис. 2 Кривая распределения вероятностей.
Кривая распределения имеет три характерные точки на оси абсцисс (рис. 2).
Точка 1 - центр распределения, соответствует среднеарифметическому значению ряда (ордината проходящая через эту точку, называется центральной); точка 2 - медиана, делит ряд на две равные части; точка 3 - мода, соответствует члену ряда, имеющему наибольшую частоту (модальная ордината).
Если центральная, медианная и модальная ординаты совпадают и образуют ось симметрии, кривую распределения называют симметричной. Наоборот, в асимметричных кривых эти ординаты не совпадают. Расстояние d между центральной и модальной ординатами, называемое радиусом асимметрии. характеризует степень асимметричности кривой.
Гидрологические явления (распределение годового, максимального, минимального стока и др.) обычно характеризуются положительным асимметричным распределением: Мода и медиана лежат левее центральной ординаты.
Параметры кривых. Параметрами аналитических кривых распределения и кривых обеспеченности являются: средний годовой сток (Q0), среднеквадратическое отклонение (s Q ), изменчивости (вариации) (Cv), коэффициент асимметрии (Cs) и коэффициент автокорреляции.
Методы вычисления Cv и Cs з ависят от коэффициента изменчивости: а) при C v< 0.5 применяется метод моментов; б) при С v > 0.5 используется метод наибольшего правдоподобия, в) графо-аналитический метод применяется в случае использования биноминальной кривой обеспеченности при любом значении Сv.
Применение эмпирических и аналитических кривых к расчетам стока. Для построения эмпирической кривой обеспеченности необходимо величины годового стока расположить в убывающем порядке от наибольшего значения к наименьшему. Такой ряд дает общее представление о колебании значений годового стока за период наблюдений.
Обеспеченность каждого члена ряда, расположенного в убывающем порядке, выраженная в процентах (или в долях единицы), может быть вычислена по формуле
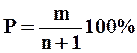
| (32) |
где Р - обеспеченность данного расхода в процентах, m -порядковый номер данного расхода в ряду, n- общее число членов ряда.
В последнее время для построения эмпирических кривых обеспеченности годового стока получил большее распространение, как более обоснованная формула

| (33) |
Эмпирическая кривая обеспеченности может быть построена в прямоугольных координатах или специальной сетке так называемой клетчатке вероятностей. По оси ординат откладываются значения годовых расходов (или модульных коэффициентов), а по оси абсцисс - значения обеспеченности (в процентах) этих расходов, вычисленные по формулам (32) или (33). Нанесенные точки соединяются плавной кривой.
Как видно из формул (32) и (33), обеспеченность крайних точек является наименее достоверной и наименее устойчивой из всех точек. И зависит от длительности ряда наблюденй. Предпочтительнее строить кривую обеспеченности на клетчатке вероятностей. При этом кривые распрямляются.
Эмпирическая кривая обеспеченности позволяет определять расчетные значения гидрологической характеристики Qр, заданной вероятности превышения Р.

| (34) |
где Кр - ордината кривой обеспеченности, соответствующая заданному значению Р%; Q0 - среднее арифметическое значение (норма) гидрологической характеристики.
Зная эмпирическую обеспеченность гидрологической характеристики, можно подсчитать вероятность повторяемости в годах, т.е. число лет N, в течение которых данное значение характеристики встречается в среднем один раз. Обеспеченность Р и повторяемость N связаны между собой следующим образом.
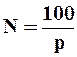 при Р< 50% (35)
при Р< 50% (35)
 при Р> 50% (36)
при Р> 50% (36)
Полученная на основе ограниченного числа фактических наблюдений эмпирическая кривая обеспеченности недостаточно точно и полно отражает закономерности изменения гидрологической характеристики. Особенно слабо освещены данными наблюдений концевые участки кривой, относящиеся к области больших и малых значений исследуемой характеристики стока, представляющие как раз наибольший интерес при решении ряда инженерных задач (например, при расчетах максимального и минимального стоков). Поэтому в гидрологии широко применяют аналитические (то есть, описываемые определенными уравнениями) функции распределения, которые наилучшим образом отвечают не только случайным выборкам, но и всему процессу колебаний характеристик стока в целом (генеральной совокупности).
Аналитические кривые обеспеченности при известных параметрах Q0, Cv и Cs строят с помощью таблиц, приведенные в работе "Практикум по гидрологии, гидрометрии и регулированию стока. М.; Агропромиздат,1998"(Приложение 2, с.215). В данной работе представлены результаты интегрирования соответствующих кривых распределения. Ординаты кривой обеспеченности, представленные в этих таблицах даны в виде модульных коэффициентов для значений обеспеченности P% от 0,001 до 99,9 % при различных коэффициентах вариации Cv - от 0,1 до 1,0.
Ординаты аналитических кривых обеспеченности определяют следующим образом:
1. Выбирают таблицу соответствующую определенному соотношению Cs/Cv.
2. По выбранной таблице для заданного коэффициента вариации Cv выписывают значения KP при различных значениях P%. Если заданный коэффициент вариации Cv не совпадает с табличным, то проводят интерполирование.
3. Определяют абсолютные ординаты кривой обеспеченности
QP=KPQ0
По вычисленным ординатам строят график аналитической кривой обеспеченности трехпараметрического гамма распределения.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 578; Нарушение авторских прав?; Мы поможем в написании вашей работы!