Лекция №3. Дифференциальное уравнение теплопроводности

Дифференциальное уравнение теплопроводности.

Процесс теплопроводности относится к числу сложных процессов, описываемых большим числом переменных параметров. Основной задачей его является определение температурного поля, получая зависимость параметров, определяющих процесс. Для этого используют методы математической физики, который основан на следующих понятиях:

1) ограничивается рассматриваемый промежуток времени;

2) из всего пространства, в котором определяется процесс, рассматривается лишь элементарный объем. Это позволяет в пределах рассматриваемого эл- го объема и промежутка времени пренебречь влиянием некоторых вторичных величин, хар-щих процесс, и, в итоге, существенно упростить зависимость, позволяющую выделить главные связи.

Но выбранный элементарный объем dV и промежуток времени d t с математической позиции являются величинами бесконечно малыми (б.м.), однако с физических позиций эти величины достаточно большие, чтобы в их пределах можно было игнорировать дискретное строение среды и рассматривать ее как континуум.

Полученная на основе такого подхода зависимость называется дифференциальным уравнением процесса, а если рассматривать теплопроводность то получим диф. уравнение теплопроводности.

Рассмотрим произвольное тело произвольных размеров с произвольным распределением температуры, кроме того, будем считать, что в теле действуют внутренние источники теплоты. К таким телам относятся радиоактивные вещества, проводники электричества под напряжением, химически реагирующие среды (с выделением теплоты – положительные источники, с поглощением - отрицательные). Помимо других параметров они характеризуются мощностью источника выделения q_v[Вт/м³] (q_v>0-положительный источник, q_v<0 - отрицательный).Будем считать, что в расматриваемом теле теплота выделяется, т.е. q_v>0.

dV Сделаем ряд допущений:

d t q_v 1) рассматриваемое тело однородно и изотропно;

2) плотность (r) и теплоемкость (с) постоянны и не зависят от координат, времени и температуры;

3) деформации (DV) объема тела (V), связанные с изменением его температуры является очень малыми по сравнению с самим телом:

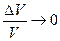, следовательно, процесс является изохорическим;

4) внутренние источники теплоты (q_v) распределены в теле равномерно.

Вывод основан на законе Фурье и первом законе термодинамики.

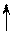
Z

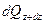
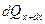
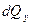
1.

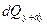
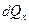
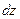
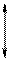
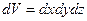
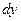
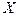
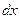
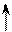
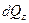
Y

Выделим в элементарном объеме dV параллелепипед и расположим его таким образом, чтобы его грани были параллельны соответствующим координатным осям.

Закон сохранения энергии сформулируем в следующем виде:

Сумма количеств теплоты, полученных элементарным объемом dV(далее - просто dV) за промежуток времени dt (далее - просто dt) извне вследствие теплопроводности dQ₁,а также из внутренних источников теплоты dQ₂ равно изменению внутренней энергии dU вещества, содержащегося в элементарном объеме dV.

dQ₁+ dQ₂= dU (1).

Рассмотрим первое слагаемое левой части уравнения (1):

обозначим количество теплоты, подведенное к граням dV за dt в направлении соответствующих осей за dQ_x –оси x, dQ_y –оси y и соответственно dQ_z –оси z, а количество теплоты, отведенной от граней dQ_x+dx, dQ_y+dy, dQ_z+dz, тогда выражения для них запишутся в виде:

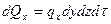
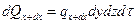
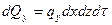
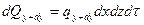
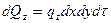
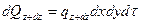
где q_x –проекция вектора плотности теплового потока на ось x, аналогично q_y и q_z.

Рассмотрим направление оси x:

Разность количеств теплоты подводимого и отводимого от соответствующих граней равно:

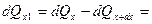
функция q_x+dx является непрерывной в промежутке dx и может быть разложена в ряд Тейлора, (это свойство следует из континуума среды):

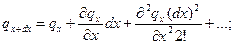
если ограничится первыми членами разложения, то тогда:

;

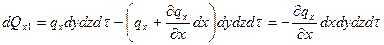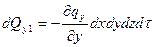проделав те же операции относительно осей y и z, получим:

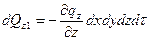
Общее количество теплоты за счет теплопроводности dQ₁:

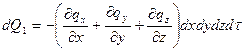;[В. М.1]

Рассмотрим dQ₂, за счет внутренних источников теплоты:

.

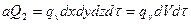Рассмотрим правую часть (1):

Из курса термодинамики нам известно:

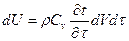,где r - плотность, С_v – изохорическая теплоемкость единицы массы [Дж/кг×°К].

Подставив dQ₁, dQ₂, dU₃ в (1), получим:

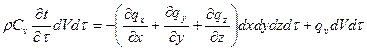; (2)

проведя несложные преобразования, получим уравнение теплопроводности в векторной форме:

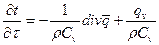(3).

Полученное уравнение можно преобразовать с использованием закона Фурье, а также с учетом несжимаемости тела С_v»C.

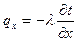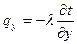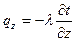; ; ,подставив значения в (2), получим:

;

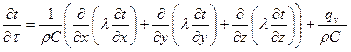в векторной форме это уравнение имеет вид:

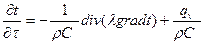(4)-дифф. уравнение теплопроводности Фурье-

Кирхгофа.

Физический смысл заключается в том, что устанавливается связь между пространственным и временным изменением температуры в любой точке тела, в которой происходит процесс теплопроводности.

Дата добавления: 2014-01-07