Граничные условия четвертого рода

Эти условия характеризуют условия теплообмена системы тел находящихся в идеальном тепловом контакте то есть процессу теплообмена нет сопротивления (свободный теплообмен).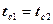

имеет место равенства тепловых потоков проходящих через соприкосновение .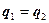

Из закона Фурье следует

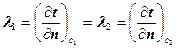
Теплопроводность при стационарном режиме и отсутствии внутренних источников теплоты. Теплопроводность однородной пластины или стенки при граничных условиях первого рода.

Рассмотрим однородную и изотропную плоскую стенку толщиной 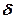и коэффициент теплопроводности .

t

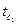
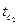
x

d

кроме того будем считать, что протяженность толщины намного больше толщины стенки 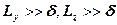в этом случае условия теплообмена на ее торцах

не влияют на распределение температур в рассматриваемом течении 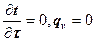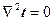при заданных условиях однозначности можно считать, что температура в теле является функцией одной координаты.

Дифференциальное уравнение процесса может быть записано

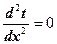(1)

Для того чтобы сформулировать полное описание процесса необходимо сформулировать условия однозначности

1. Г.У. , .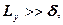

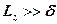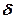2. Ф.У. , .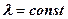

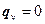3. временные условия не задаются.

4. Граничные условия первого рода

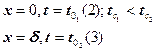
В результате решения поставленной задачи должно быть найдено распределение температур системы или температурное поле.

Формула для определения теплового потока через данное тело.

Закон распределения температуры в теле мы найдем в результате интегрирования дифференциального уравнения процесса при данных граничных условиях

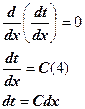
(5) – общее решение используя условия (2) и (3) составляем уравнение

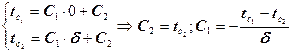
Подставив значение констант в общее уравнение (5) получим закон распределения температуры плоской стенки

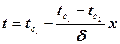(6)

Формулу для определения теплового потока получаем используя закон Фурье

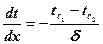
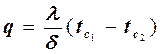(7)

Следует: количество теплоты, что передается через единицу времени будет прямопропорциональна коэффициенту теплопроводности и обратнопропорциональна толщине стенки.

Запишем уравнение (7) следующим образом

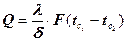
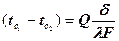сравним с законом Ома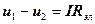

- термический коэффициент процесса теплопроводности

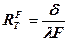
- представляет собой падение температуры на единицу плотности теплового потока

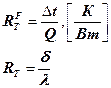
- удельный коэффициент процесса теплопроводности

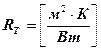
Из выражения (7) следует, что , .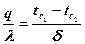

Теплопроводность плоской стенки при

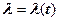
Для многих материалов зависимость коэффициента теплопроводности от меры близка к линейной

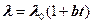
где 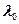- значение коэффициентов теплопроводности при 0⁰С.

На основе закона Фурье

(1)

Разделим переменные и интегрируя выражение (1) в пределах от 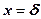и в интервале температур от 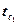до 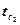получим

(2)

В выражение (2) множитель 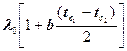является среднеинтегральной величиной коэффициента теплопроводности, то есть

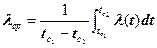
При этом плотность теплового потока на поверхности пластины

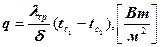(4)

Из (4) следует, что если коэффициент теплопроводности зависит от температуры то 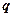можно вычислить в предположении, что 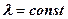, принимая для него среднее интегральное значение в интервале температур 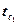и .

И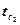нтегрируя выражение (1) в пределах от 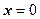до любой текущей координаты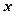

и в интервале температур от 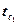до 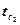получаем выражение для температурного поля

Из этого следует, что температура в стенке изменяется не линейно, а по кривой определенную знаком и численным значением коэффициента .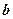

Лекция №5.

Дата добавления: 2014-01-07