Решение уравнения Абеля

Умножим левую и правую части уравнения (2.4) на величину

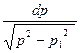
и проинтегрируем по p в пределах от p=p ₁ до p=η ₀ , в результате получим:

Здесь p 1 – постоянный параметр фиксированного луча, выходящего на расстоянии x₁ от источника, а p – переменный параметр, удовлетворяющий условию:

p>p 1. (2.5)

С физической точки зрения мы интегрируем здесь по лучам, лежащим выше луча с параметром p 1.

Неравенство (2.5) будет выполняться в силу принятого условия о монотонном возрастании скорости с глубиной. Найдем область интегрирования в правой части интегрального уравнения.

Рис. 2.11.

Интегрирование здесь применяется сначала по η, а потом по р. Пределы внутреннего интеграла

η=p – (p - переменно),

η= η₀ – указывают границы изменения η. Имеем (рис.2.11) пределы внешнего интеграла

p=p _1, p= η_0. Они дают границы, в которых может изменяться p. Мы не можем произвести первое внутреннее интегрирование, так как под знаком интеграла стоит неизвестная функция 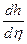. Поэтому изменим порядок интегрирования. В результате получим:

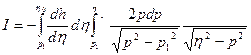
Через I обозначена правая часть интегрального уравнения.

Покажем, что в этом уравнении внутренний интеграл равен π.

Проще всего в этом можно убедиться с помощью подстановки:

Находим новые пределы интегрирования

p = p ₁ t = 0

p = η t = 1

Для преобразования интегральной функции найдем следующие вспомогательные величины

p - p ₁² =t (η ²- p ₁² ),

η ² - p ² = (η ² - p ₁² ) (1 -t). (2.6)

Второе равенство можно получить следующим образом из равенства (2.6):

Продифференцируем первое равенство, получим:

2 pdp = (η ² - p ₁² )dt

Интеграл преобразуется теперь так

Уравнение примет вид

В правой части уравнения возвратимся к интегрированию по старой переменной h. Учитывая, что

и далее получаем

(2.7)

Интегрируем по частям интеграл, стоящий в правой части уравнения:

(2.8)

Из уравнений (2.7) и (2.8) получаем окончательный вид формулы Чибисова.

. (2.9)

где

Интеграл в правой части (2.9) вычисляется методами численного интегрирования. Можно применить любую известную формулу приближенного вычисления определенного интеграла.

Дата добавления: 2014-01-07