Взаимодействие симметрических операций

(элементов симметрии)

Работая с кристаллами, исследователи обратили внимание на то, что элементы симметрии располагаются в них не случайно, а определенным закономерным образом. Действительно, сочетания элементов симметрии, как было показано выше, и их взаимные расположения подчиняются всем положениям математической теории абстрактных групп.

Рассматривая взаимодействия матриц, каждая из которых отражает определенную симметрическую операцию, можно убедиться в том, что произведение двух матриц приводит к появлению третьей — результирующей матрицы. Иными словами, произведение, или взаимодействие, двух симметрических операций порождает третью результирующую операцию, а следовательно, и элемент симметрии. Рассмотрев все взаимодействия элементов симметрии данного кристалла, можно получить полную совокупность симметрических операций, называемую группой симметрии (или классом в кристаллографии).

Вывод групп симметрии впервые был осуществлен в 1826 г, немецким кристаллографом М. Л. Франкенгеймом, затем независимо от него в 1830 г. немецким минералогом И. Ф. Гесселем. Однако их работы были не поняты и забыты современниками. И лишь в 1867 г. Петербургский академик А. В. Гадолин осуществил их строгий математический вывод и показал, что существует всего 32 класса симметрии, полностью описывающие все возможные для кристаллов комбинации известных элементов симметрии.

Зная основные правила взаимодействия элементов симметрии (правила умножения симметрических операций), нетрудно вывести все возможные их сочетания. Рассмотрев взаимодействия симметрических операций в общем виде, увидим, что если оба элемента симметрии 1рода (связывающие конгруэнтно равные фигуры — П с П или Л с Л), то асимметричная исходная фигура дважды преобразуется в конгруэнтную № и заменить эти две операции симметрии (т. е. совместить исходную фигуру с конечной) может лишь операция I рода — простой поворот:

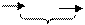П ^1р П ^1р П

1р

При сочетании двух операций симметрии II рода (связывающих зеркально равные — энантиоморфные — фигуры — П с Л) начальная П- фигура под действием операции симметрии II рода преобразуется в энантиоморфиую (Л), а затем под действием второй (также операции II рода) будет переведена в конгруэнтную исходную фигуру (П). Следовательно, заменить две проведенные операции II рода, т. е/ связать конгруэнтные исходную и результирующую — фигуры, сможет лишь операция симметрии 1рода — простой поворот;

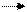
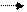
П ^1Iр П ^IIр П

1р

Если же последовательно действуют операции разнородные (I и II родов), то результирующей окажется операция II рода, являющаяся результатом действия двух разнородных исходных симметрических операций (движений):

П ^1р П ^IIр П

IIр

Результирующим элементом симметрии в данном случае окажется сложный элемент симметрии II рода, задающий две симметрические операции, одной из которых будет операция I рода — поворот, а второй — операция II рода — отражение в плоскости симметрии либо инверсия в точке симметрии. Таким сложным элементом симметрии будет либо зеркально-поворотная ось симметрии — если поворот на некоторый угол вокруг оси сопровождается отражением в плоскости симметрии, перпендикулярной оси вращения, либо инверсионная ось, — когда поворот сопровождается отражением в центре инверсии, находящемся на этой оси.

Дата добавления: 2014-01-07