Сферическая проекция

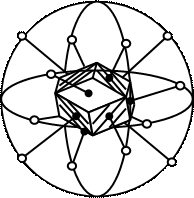
Опишем вокруг точки О сферу (рис.5.14). Пересечение нормалей к граням к граням кристалла с поверхностью сферы представляет собой сферическую проекцию нормалей граней кристалла. Полученные точки на сфере проекций называют полюсами граней. Каждой из точек сферической проекции соответствует одна из граней кристалла (рис. 5.15). Сферическую проекцию кристалла можно строить, не заменяя грани кристалла их нормалями. В этом случае все грани кристалла путем параллельного переноса перемещают в центр сферы проекции и строят следы пересечения этих граней со сферической проекцией. Каждая такая сферическая проекция представляет собой дугу большого круга.

Положение любой точки на поверхности сферы можно охарактеризовать двумя сферическими координатами: широтой и долготой. Широта (полярное расстояние) отсчитывается по любому направлению от нуля (северный полюс) до 180 (южный полюс), долгота – по экватору от меридиана, принятого за нулевой (рис. 5.16).

Между индексами плоскостей (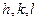) и сферическими координатами и нормали к этой плоскости существует строгая математическая зависимость. Вид зависимости отличен для разных сингоний и расположений кристалла. Для кубической сингонии при условии, что одна из плоскостей куба (001) находится в плоскости проекций:

, ,

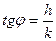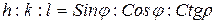
Сферическая проекция кристалла наглядна, но практика показала, что её удобнее проектировать на плоскость. При этом пользуются стереографическими, гномостереографическими проекциями.

Рис. 5.15.Принцип построения сферической проекции.	Рис.5.16 Сферические координаты на поверхности сферы проекции

Дата добавления: 2014-01-07