
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Трансляционная группа, базис ячейки
|
|
|
|
Тип ячейки Бравэ.
| Сингония | Тип решетки | ||||
| Примитивная | Базоцентри-рованная | Объемно- центрированная | Гранецинтри-рованная | ||
| Триклинная | 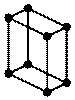 Р Р
| ||||
| Моноклинная | 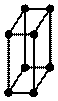 Р Р
| 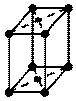 С С
| |||
| Ромбическая |  Р Р
|  С С
| 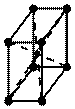 I I
|  F F
| |
| Тригональная (робоэдрическая) | 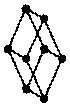 R R
| ||||
| Тетрагональная | 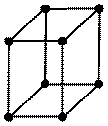 Р Р
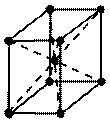
| 
| |||
| Гексагональная |  Р Р
| ||||
| Кубическая | 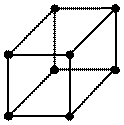 Р Р
| 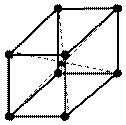 I I
|  F F
| ||
Приняв один из узлов пространственной решетки за начало координат, т. е. за узел с символом [[000]], можно найти все остальные узлы решетки с помощью трансляционной группы — совокупности основных трансляций элементарной ячейки.
Трансляционная группа Г для примитивной ячейки состоит из трансляций а, b, с, соответствующих ребрам элементарной ячейки. Для примитивных решеток достаточно определить три основные трансляции, а для всех остальных решеток нужно учитывать еще дополнительные трансляции.
Чтобы выделить в структуре элементарную ячейку Бравэ, надо найти три кратчайшие непараллельные трансляции a, b, c, причем каждая трансляция должна начинаться и кончаться на одинаковых узлах. Далее надо проверить основные требования:
1)можно ли на этих трансляциях построить ячейку, отвечающую правилам выбора ячейки Бравэ;
2) все ли частицы в структуре можно получить с помощью такого набора трансляций.
В общем случае каждой сингонии могут отвечать решетки всех четырех типов (Р, С, I, F), однако на деле во всех сингониях, кроме ромбической, число возможных решеток Бравэ сокращается за счет сведения одних типов решеток к другим. Так, например, в кубической сингонии не может быть базоцентрированной решетки: если пара граней кубической элементарной ячейки оказывается центрированной, то на основании кубической симметрии центрируются все остальные грани и вместо базоцентрированной получается гранецентрированная решетка.
В триклинной сингонии все непримитивные решетки (С, I, F) сводят к примитивной, выбирая по-другому элементарную ячейку; например, объемно-центрированную решетку с трансляциями (а+b+с)/2, b, с можно свести к примитивной с трансляциями:  ,
, 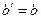 ,
,  базоцентрированную — к примитивной с вдвое меньшей элементарной ячейкой.
базоцентрированную — к примитивной с вдвое меньшей элементарной ячейкой.
14 решеток Бравэ распределяются по сингониям, как показано (табл. 2).
Совокупность координат узлов, входящих в элементарную ячейку, называется базисом ячейки. Всю кристаллическую структуру можно получить, повторяя узлы базиса совокупностью трансляций ячейки Бравэ. При этом начало координат выбирается в вершине ячейки и координаты узлов выражаются в долях элементарных трансляций а, b, с. Например, для примитивной ячейки достаточно указать координаты узла [[000]], а все остальные узлы можно получить из этого узла, повторяя его с помощью основных трансляций.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1184; Нарушение авторских прав?; Мы поможем в написании вашей работы!