Смешанные дислокации и их движение

Дислокация не может закончиться внутри кристалла, не соединяясь с другой дислокацией. Это следует из того, что граница зоны сдвига всегда является замкнутой линией. Часть этой гра­ницы может проходить по внешней поверхности кристалла. Следовательно, линия дислокации должна замыкаться внутри кристалла или оканчиваться на его поверхности. Здесь возможны самые разнообразные варианты.

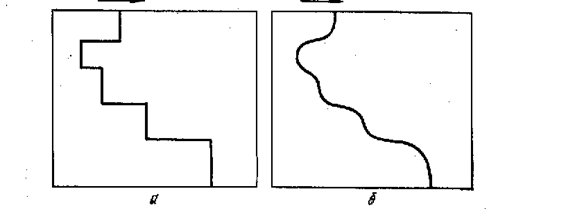
Рис. 9.14. Краевые и винтовые дислокации образуют одну не­прерывную ломаную (а) или плавную (б) линию внутри кристалла. Плавная линия содержит также участки смешан­ной ориентации

На рис. 9.14, а линия дислокации состоит из прямых участков краевой и винтовой ориентации, перпендикулярных и параллель­ных вектору сдвига соответственно. Это частный случай.

В более общем случае в плоскости скольжения линия дислока­ции —кривая (рис. 9.14,6). Отдельные малые участки этой кривой имеют краевую или винтовую ориентацию, но большая ее часть не перпендикулярна и не параллельна вектору сдвига; в послед­нем случае мы имеем дело с дислокацией смешанной ориентации, которая в макро масштабе является плоской кривой.

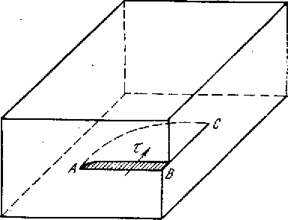
Рис. 9.15. Сдвиг, создавший смешанную дислока­цию АС

Рассмотрим схему атомного строения кристалла со смешанной дислокацией. На рис. 9.15 линия АС ограничивает внутри кри­сталла зону сдвига АВС. Заштрихована ступенька, образовав­шаяся на передней грани кристалла при сдвиге верхней его части относительно нижней по площади АВС. Расположение атомов вдоль линии АС показано на рис. 9.15, где плоскость чертежа является плоскостью скольжения; черные кружки обозначают атомы под этой плоскостью, а белые — над ней. Вблизи точки А на участке АА' дислокация параллельна вектору сдвига и, следо­вательно, имеет винтовую ориентацию. Вблизи точки С дислокация перпендикулярна вектору сдвига и, следова­тельно, имеет краевую ориентацию. Вблизи точки С в верхней части кристалла (над плоскостью чертежа) имеется сгущение вертикальных атомных плоскостей и экстраплоскость.

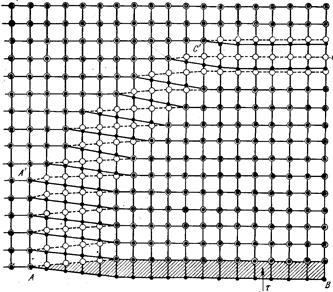
Рис. 9.16 Расположение атомов в области смешанной дислокации. Схема получена при рассмотрении на рис. 10 плоскости АВС со стороны верхней грани кристалла

В отличие от рис.9.2, где мы смотрим на экстраплоскость с ее торца, на рис. 9.15 экстраплоскость рассматривается сверху. Здесь она видна в виде цепочки светлых кружков СС', внутри которых нет черных кружков. Эта цепочка атомов является краем экстраплоскости. Вблизи точки C^/ экстраплоскость искривляется и соединяется с вертикальной плоскостью, находящейся под плоскостью сколь­жения, т. е. экстраплоскость здесь перестает быть неполной атомной плоскостью (экстраплоскостью), и дислокация теряет краевую ориентацию. В промежутке между чисто краевым участ­ком вблизи точки С и чисто винтовым вблизи точки А дислокация имеет смешанную ориентацию, промежуточную между краевой и винтовой. Под действием приложенных касательных напряжений τ зона сдвига, заштрихованная на рис. 16, расширяется. Участок дисло­кации с чисто краевой ориентацией вблизи точки С скользит в направлении приложенной силы, а участок с чисто винтовой ориентацией вблизи точки А—перпендикулярно этому направле­нию. Когда вся линия смешанной дислокации выйдет на внешние грани, верхняя часть кристалла окажется сдвинутой относительно нижней в направлении действующих касательных напряжений на один период решетки. Ясно, что в общем случае отдельные участки смешанной дислокации выходят на поверхность кристалла неодновременно.

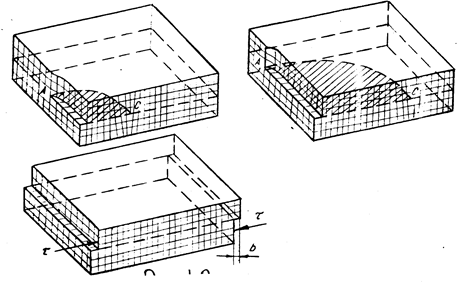
Рис. 9.17. При скольжении смешанной дислокации АС через весь кристалл верхняя часть его сдвинулась относи­тельно нижней на одно меж­атомное расстояние

На рис. 9.17,б и 9.18 линия смешанной дислокации оканчивается на гранях кристалла. Но она может образовывать и замкнутые плоские петли внутри кристалла. Отдельные участки дислокацион­ной петли имеют чисто краевую или чисто винтовую ориентацию, а большая часть — смешанную ориентацию.

Плоская петля смешанной дислокации, как и любая дислока­ция, является границей зоны сдвига. Если вектор сдвига нахо­дится в плоскости петли, то петля отделяет область плоскости скольжения внутри нее, где сдвиг уже прошел, от области, лежа­щей вне петли и еще не охваченной сдвигом. Скольжение разви­вается при расширении петли. Возможен и противоположный случай, когда область, где сдвиг уже прошел, находится вне петли дислокации. Скольжение в этом случае развивается при сужении петли. Дислокационные петли играют важную роль в процессах пластической деформации.

Из-за наличия участков с винтовой ориентацией дислокацион­ная петля может совершать поперечное скольжение. На рис. 9.18,а показана дислокационная петля, распространявшаяся в плоскости (111) г.ц.к. решетки. Участок петли вблизи точки т, имеющий винтовую ориентацию, из-за встречи с препятствием в плоскости (111) или по другой причине может «соскользнуть» по плоскости поперечного скольжения (111), находящейся под углом к перво­начальной плоскости скольжения (рис. 9.18,б). Затем участок петли с винтовой ориентацией способен из плоскости (111) перейти в атомную плоскость, параллельную первоначальной плоскости скольжения (рис. 9.18, в). Многократное повторение этого процесса является множественным поперечным скольжением. В результате петля смешанной дислокации перестает быть плоской. Так как винтовая дислокация легко переходит из одной плоскости в другую, то в общем случае и линия смешанной дислокации и поверхность скольжения не лежат в одной плоскости.

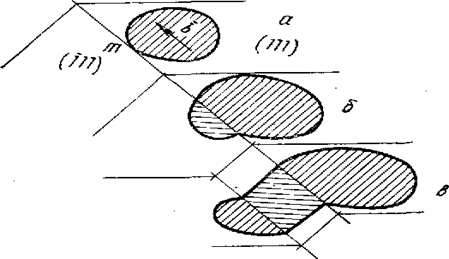
Рис. 9.18 Поперечное и двойное поперечное скольжение петли смешанной дислокации в г.ц.к. решетке.

Контрольные вопросы

1. Дайте определение дислокации.

2. Объясните наиболее простой способ введения дислокации в кристалл.

3. Дайте понятие критически скалывающего напряжения.

4. Укажите расположение линии краевой дислокации по отношению к касательному напряже­нию.

5. Объясните механизм скольжения краевой дислокации.

6. Объясните, почему скольжение дислокации называют консервативным движением.

7. Укажите, по какой плоскости происходит скольжение краевой дислокации.

8. Дайте определение механизма переползания краевой дислокации.

9. Объясните, какие факторы влияют на скольжение краевой дислокации.

10. Объясните, какие факторы влияют на переползание краевой дислокации.

Объясните варианты положительного и отрицательного переползания краевой дислока­ции.

11. Объясните, почему переползание относят к диффузионному процессу.

12. Дайте понятие порога на линии дислокации.

13. Укажите отличия положительной и отрицательной краевой дислокации.

14. Укажите, в каком направлении по отношению к касательному напряжению скользит винто­вая дислокация.

15. Объясните, может ли скользить смешанная дислокация.

Дата добавления: 2014-01-07