Энергия дислокации

План лекции

Лекция 11. Упругие свойства дислокаций

Плотность дислокаций

Важная характеристика дислокационной структуры - плот­ность дислокаций - суммарная длина всех линий дислокаций в единице объема. Плотность дислокаций в единице объёма, см^-2

ρ = (∑ l /V), (10.4)

где ∑ l —суммарная длина всех линий дислокаций в кристалле, см; V—объем кристалла, см³.

Плотность дислокаций определяют и как число дислокаций, пересекающих единицу площади, например единицу площади металлографического шлифа. Оба способа подсчета плотности дислокаций в общем случае дают разные значения.

Плотность дислокации зависит от способа и режима обработки металла. Ниже для металлов в разных состояниях приведены типичные значения плотности дислокаций, см ^-2:

Тщательно выращенный массивный монокристалл очень

высокой чистоты <10³

Отожженный обычный монокристалл 10⁴—10⁶

Отожженный поликристалл 10⁷—10^s

Металл после сильной холодной деформации 10¹¹—10¹²

В монокристаллических усах дислокации или совсем отсутствуют, или же в одном монокристалле находится только одна дислокация.

Полупроводниковые кристаллы кремния и германия, даже массового промышленного производства, имеют сравнительно низкую плотность дислокаций (10³—10⁴ см ^-2).

От плотности дислокаций зависит большинство технически важных свойств металлов и сплавов. Плотность дислокаций, которая может быть разной в различных микроучастках материала, влияет на механизм, скорость и направление структурных изменений.

Контрольные вопросы

1. Опишите механизм введения в кристалл призматической дислокации.

2. Объясните возможности перемещения призматической дислокации.

3. Объясните, что такое вектор Бюргерса.

4. Объясните, что такое контур Бюргерса.

5. Укажите расположение вектора Бюргерса относительно линий краевой и винтовой дислока­ций.

6. Запишите, чему равна мощность вектора Бюргерса.

7. Дайте определение плотности дислокации и запишите размерность.

8. Укажите параметры, влияющие на плотность дислокаций.

9. Покажите разложение вектор Бюргерса смешанной дислокации на краевую и винтовую компоненты.

1. Энергия дислокации

2. Силы, действующие на дислокацию

3. Упругие взаимодействия параллельных краевых дислокаций

4. Упругое взаимодействие параллельных винтовых дислокаций

Дислокация повышает энергию кристалла. Она—центр поля внутренних напряжений, убывающих с увеличением расстояния от дислокации. В ядре дислокации смещения атомов настолько велики, что рассчитать энергию здесь с помощью методов теории упругости не удается. За пределами ядра дислокации деформации описываются линейными уравнениями теории упругости, и поле напряжений и соответствующую энергию легко вычислить.

Для оценки энергии винтовой дислокации введем допущение, что в процессе ее образования кристалл ведет себя как упругое изотропное тело. Возьмем такой совершенный кристалл, сделаем в нем несквозной надрез и сдвинем две части этого кристалла одну относительно другой по плоскости надреза на величину b так, как это уже рассматривалось на рис. 26. Такой сдвиг про­исходит под действием касательных сил и соответствующих на­пряжений в плоскости надреза. Работа, совершенная этими силами для создания смещения b, равна энергии винтовой дисло­кации:

,

где τ — касательное напряжение, вызывающее сдвиг на вели­чину b.

В период сдвига напряжение линейно возрастает от 0 до τ. Поэтому при расчете энергии сдвига необходимо брать среднюю за весь период сдвига величину касательного напряжения, равного τ/2. Произведение этого напряжения на площадь ds, по которой происходит сдвиг, даст силу сдвига, а произведение силы сдвига на величину смещения дает искомую работу сдвига. Но касатель­ные напряжения на разном расстоянии от оси дислокации раз­личны (они убывают с увеличением этого расстояния). Поэтому приходится брать интеграл касательных напряжений по всей площади сдвига.

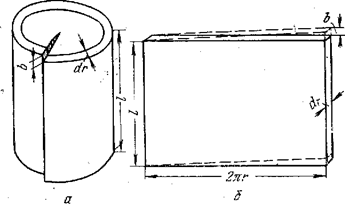
Рис. 11.1. Цилиндрическая оболочка вокруг винтовой дислокации, развернутая в пластину

Для расчета касательных напряжений используем следующий прием. Мысленно подразделим кристалл на ряд цилиндрических слоев с общей осью. Возьмем один такой цилиндрический слой (рис. 11.1, а) с радиусом r и толщиной dr, разрежем его вдоль образующей цилиндра l с одной стороны и сместим на величину b одну часть этого слоя по отношению к другой. При условии, что толщина слоя мала, величина силы, препятствующей указанному смещению, не изменится, если цилиндрический слой развернуть в плоскую пластину (рис. 11.1,б).

Для малых сдвиговых деформаций справедлив закон Гука:

τ = Gb/2πr (G—модуль сдвига). Это касательное напряжение действует на площадке ds = Idr, Тогда

;

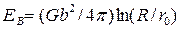(11.1)

В этом выражении: G—модуль сдвига; b—вектор Бюргерса дислокации; I — ее длина; r_o - радиус ядра дислокации (несколько межатомных расстояний); R — расстояние, на которое распространяется упругая деформация от дислокации.

Далее везде под энергией дислокации будем понимать - связанную с ней упругую энер­гию кристалла, приходящуюся на единицу длины дислокации. Следовательно:

Ев = (Gb ²/4π) ln(R/r₀). (11.2)

Расчет энергии краевой дислокации более сложен, так как поле напряжений вокруг нее не обладает цилиндрической симмет­рией, как поле вокруг винтовой дислокации (с одной стороны от плоскости скольжения — растяжение, а с другой — сжатие).

Энергия краевой дислокации:

Eкр=[Gb²/4π(1-μ)] ln(R/r₀), (11.3)

где μ - коэффициент Пуассона, а остальные величины те же, что и в формуле (11.1), Приняв типичное для металлов значение μ=1/3, получим, что энергия краевой дислокации в 1,5 раза больше энергии винтовой дислокации. Этим различием в боль­шинстве оценочных расчетов можно пренебречь.

Большинство дислокаций в реальных металлах — смешанные. Вектор Бюргерса смешанной дислокации можно разложить на краевую и винтовую компоненты: bкр=bсм sinφ, bв= bсм cosφ. Используя формулы (11.2) и (11.3), представим энер­гию смешанной дислокации как сумму энергий краевой и винто­вой дислокаций с указанными векторами Бюргерса: (11.4)

Есм = Екр +Ев = (Gb²см sin²φ /4π) In (R/r₀) + [Gb²см cos²φ / (1-μ)]). In R/r₀

Отсюда получаем

Есм = [Gb²см/4π(1 μ -)] (l-μcos²φ) In R/r₀

При φ = 0° это выражение преобразуется в формулу (11.1), а при φ =90°-в формулу (11.3). Следовательно, в зависимости от угла наклона вектора Бюргерса к линии смешанной дислокации ее энергия является промежуточной между значениями энергии краевой и винтовой дислокаций.

Энергия дислокации зависит от расстояния R, на которое от нее распространяется упругая деформация. Максимальное зна­чение R ограничено размерами кристалла. Обычно R принимают равным половине среднего расстояния между соседними дислока­циями. Для оценочных расчетов весьма благоприятно то, что энергия дислокаций очень слабо зависит от величины R в реаль­ных кристаллах. Так, например, если увеличить R с 1 мкм до 1 см, т. е. в 10000 раз, то энергия винтовой дислокации в кристалле должна возрасти лишь в 2,3 раза. Для наиболее типичных интервалов значений R, r₀ и μ формулы приобретают вид, очень удобный при оценках энергии дислокации любого типа:

Е=αGb², (11.5)

где α = 0,5—1,0.

Вполне естественно, что энергия дислокации зависит от век­тора Бюргерса, характеризующего степень искаженности решетки, и от модуля сдвига, являющегося характеристикой сил межатом­ной связи. Чем больше G, тем сильнее межатомные силы сопро­тивляются смещениям атомов, т. е. больше накапливается упругая энергия искажений решетки.

Разные оценки показывают, что потенциальная энергия ядра дислокации по порядку величины не превышает одну десятую энергии, связанной с упругой деформацией за пределами ядра дислокации. Вследствие неопределенности расчетов общую энер­гию дислокации считают равной αGb². Для разных твердых тел энергия винтовых дислокаций обычно находится в пределах от 3 до 10 эВ в расчете на одно межатомное расстояние вдоль линии дислокации.

Увеличение длины дислокации приводит к росту ее упругой энергии. Поэтому линия дислокации ведет себя как упругая нить, всегда стремящаяся выпрямиться, чтобы сократить свою длину. Энергию дислокации, приходящуюся на единицу ее длины, назы­вают линейным, натяжением дислокации. Следовательно, с учетом формулы (11.5)

Т=αGb². (11.6)

Сила линейного натяжения направлена вдоль линии дисло­кации. Выше рассматривалась энергия неподвижной дислокации. Поля напряжений движущейся и неподвижной дислокаций раз­личны, что объясняется возникновением инерциальных сил от движения элементов тела, вызванного движением дислокации. Уравнения движения дислокации сходны с уравнениями движения частицы, приводимыми в теории относительности. Здесь скорость звука в данном материале является такой же предельной скоростью, как скорость света в теории Эйнштейна. С приближе­нием скорости дислокации υ к скорости звука в кристалле с энер­гия дислокации бесконечно возрастает. Энергия винтовой дислокации.

E_В=E₀ (1-v²/c²)^-1/2 (11.7)

где e₀ - энергия покоящейся дислокации.

Следовательно, дислокация не может двигаться в кристалле быстpee звука (~ 10⁵ см/с).

Как влияет скорость движения на энергию дислокации, видно из следующих примеров. При скоростях порядка с/10 и менее энергия дислокации мало отличается от энергии покоя. Повышение, скорости от нуля до с√3/2 удваивает энергию дислокации. Избыточная энергия помогает дислокации преодолевать разные препятствия в решетке реального кристалла.

Смещения атомов в ядре дислокации и упругие смещения в поле вокруг дислокации за пределами этого ядра сильно повы­шают энергию кристалла U. Вместе с тем дислокации увеличи­вают неупорядоченность и соответственно энтропийный член TS в формуле для свободной энергии (F = U—TS).

Введение дислокации увеличивает число возможных способов размещения атомов в решетке, так как дислокация может распо­лагаться в кристалле разными способами. Это обусловливает повышение конфигурационной энтропии. Возрастает также коле­бательная энтропия, так как вблизи дислокации оказывается измененной частота колебаний атомов.

Уменьшение свободной энергии при росте энтропии намного меньше, чем повышение свободной энергии вследствие образова­ния поля упругих напряжений при введении дислокации в кри­сталл. Поэтому в отличие от точечных дефектов, которые в опре­деленном числе (концентрации) являются равновесными для данной температуры, дислокации при любых температурах и в любом числе повышают свободную энергию кристалла и всегда являются термодинамически неравновесными дефектами. В отли­чие от точечных дефектов, равновесная концентрация которых растет с температурой пропорционально фактору Больцмана e^-Eo/kT количество дислокаций не зависит от температуры. Это объясняется большой величиной упругой энергии их образования. Флуктуации энергии не способны создать новую дислокацию; фактор Больцмана здесь не играет существенной роли.

Дата добавления: 2014-01-07