Источник Франка — Рида

Размножение дислокаций при пластической деформации

Увеличение плотности дислокаций на несколько порядков в ре­зультате холодной пластической деформации требует введения в теорию представлений о механизме образования дислокаций в процессе самой деформации. Кроме того, пробег одной дисло­кации через весь кристалл приводит к сдвигу по плоскости скольжения на величину вектора Бюргерса, при этом дислока­ция выходит на поверхность кристалла. Наблюдаемый же экс­периментально сдвиг на поверхности кристалла на несколько по­рядков больше величины межатомного расстояния. Имеющихся перед началом деформации дислокаций совершенно недоста­точно, чтобы объяснить такие большие сдвиги последователь­ным пробегом дислокаций по одной плоскости скольжения. Из этого следует, что в процессе деформирования образуется боль­шое число новых или, как иногда говорят, «свежих» дисло­каций.

В 150 г. Франк и Рид предложили остроумный и простой механизм размножения дислокаций в процессе пластической деформации (рис. 15.3).

Источником дислокаций является дислокация, концы кото­рой DD' закреплены. На рис. 15.3, а плоскость чертежа является плоскостью скольжения, содержащей линию дислокации DD''.

Однородные напряжения т выгибают линию дислокации в дугу (рис. 3,6), а линейное натяжение дислокации стремится ее выпрямить. В условиях, когда приложенная сила уравнове­шивает восстанавливающую, радиус дуги г определяется из со­отношения: t =aGh/r. По мере роста касательного напря­жения дуга все больше выгибается, и радиус ее уменьшается. Когда дуга становится полуокружностью, ее радиус r=l/2, где l—длина дислокации. Это минимальный радиус, и ему соответ­ствует максимальное значение касательного напряжения Ткр=2aGb/l. Принимая a=0,5, получаем

t_кр=Gb/l. (15.1)

Если в формулу (15.1) подставить значения G, Ь и 1=10^{-4 см, типичные для отожженных монокристаллов цветных металлов, то} t_кр»1 МПа. Эта величина хорошо согласуется с эксперимен­тально определенными значениями критического скалывающего напряжения.

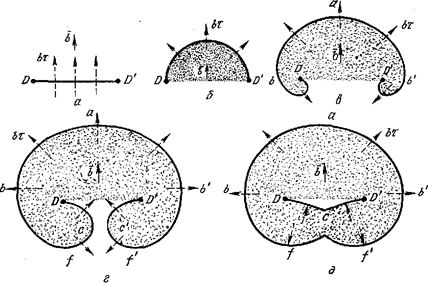
Рис. 15.3 Этапы образования дислокационной петли плоским источником Франка — Рида

При любых значениях t<t_кр дуга стабильна—определен­ному значению t соответствует определенное значение r. Если дуга еще не выгнулась в полуокружность, то при уменьшении касательного напряжения сила натяжения будет упруго выпрям­лять дугу.

Площадь, через которую продвигается линия дислокации, за­тушевана на рис. 15.3, она является зоной, где сдвиг уже про­шел. Направление касательного напряжения от приложенной силы остается все время неизменным, а сила f=bt, действую­щая на дислокацию, в каждой точке перпендикулярна линии дислокации, т. е. направлена по радиусу кривой (см. стрелки на рис. 15.3).

Выгибание дуги от r=∞ (прямая DD', рис. 15.3, а) до r=r_кр (полуокружность на рис. 15.3,6) требует непрерывного повы­шения касательного напряжения от нуля до t_кр=Gb/l. При лю­бом небольшом превышении t_кр дальнейшее расширение петли дислокации приводит к увеличению радиуса дуги, и линия дислокации оказывается в нестабильном положении — при по­стоянном напряжении от приложенной силы, которое теперь может стать и меньше ткр, дислокационная петля самопроиз­вольно расширяется, описывая все большую площадь (рис. 15.3, е, г). Поэтому напряжение, требующееся для выгибания линии дислокации в полуокружность, называют критическим.

Расширяющаяся петля остается закрепленной в точках D и D^/ и поэтому закручивается вокруг этих точек в виде двух сим­метричных спиралей под действием силы bt, все время перпен­дикулярной линии дислокации на всех ее участках (рис. 15.3, в, г). При таком закручивании обязательно наступает момент, когда две симметричные спиралевидные части дислокации со­прикасаются. В месте соприкосновения встречаются участки дислокаций противоположного знака. Они взаимно уничтожа­ются, в результате чего одна дислокация разделяется на две—­замкнутую петлю и дислокацию DCD', состоящую из двух дуг (рис. 15.3, д).

Замкнутая дислокационная петля не связана с точками за­крепления D и D'. Под действием касательного напряжения она может неограниченно распространяться во псе стороны, и, если нет других препятствий, выйти на поверхность кристалла.

Дислокация DCD', выпрямляясь под действием приложенной силы и линейного натяжения, сокращает свою длину до DD', т, е. приходит в стартовое положение исходной дислокации. По­сле этого, если продолжают действовать напряжения не меньше t_кр, новая дислокация уже рассмотренным путем образует но­вую дислокационную петлю и дислокацию DD' и т. д. Таким способом источник. Франка—Рида может генерировать неогра­ниченное число петель дислокаций в одной плоскости скольже­ния и создавать в этой плоскости значительный сдвиг.

На первый взгляд может показаться непонятным, почему при напряжении, действующем в одном и том же направлении, сначала спиральные участки дислокации, а затем замкнутая петля распространяются во все стороны, в том числе и в на­правлении, прямо противоположном действующему напряже­нию. Это легко уяснить, если обратить внимание на ориентацию разных участков линии дислокации и вспомнить о направлении движения дислокаций разной ориентатации и разного знака и о распространении дислокационной петли.

Если исходная дислокация DD' была чисто краевой, то при выгибании ее в дугу она превращается в смешанную дислока­цию. На рис. 15.3, в вблизи точки а дислокация имеет краевую, вблизи точек b и b'—винтовую, а в промежуточных точках— смешанную ориентацию. Участок краевой ориентации скользит по направлению вектора Бюргерса, а участки винтовой ориен­тации—перпендикулярно ему. Поскольку последние в точках b и b' имеют противоположные знаки, то они перемещаются под действием одной и той же силы в прямо противоположных на­правлениях. На участках вблизи точек f и f ' дислокация имеет краевую ориентацию (рис. 15.3, в). Знак краевой дислокации вблизи точек f и f ' противоположен знаку краевой дислокации вблизи точки a. Если, например исходная дислокация DD' была положительной, то участок краевой ориентации вблизи точки а также является положительной дислокацией, а участки вблизи f и f '—отрицательной краевой дислокацией. Под дей­ствием одних и тех же напряжений краевые дислокации разного знака перемещаются в прямо противоположных направлениях.

Вблизи точек с и с' участки дислокации имеют винтовую ориентацию и противоположный знак (рис. 15.3, г). Двигаясь в направлении действия на них силы bt навстречу один дру­гому, они аннигилируют.

Замкнутая петля на рис. 153, как уже указывалось, рас­пространяется во все стороны. С этим согласуется то положе­ние, что участки с краевой ориентацией а и f (а также f '), имеющие разный знак, должны скользить в противоположных направлениях под действием одного и того же напряжения. То же самое происходит с участками винтовой ориентации b и b', имеющими разный знак.

Рассмотренный источник Франка—Рида генерирует дислокационные петли в одной атомной плоскости. Наряду с таким плоским источником был предложен аналогичный по механизму пространственный источник, дислока­ций, часто называемый коническим или спиральным. Этот источник неогра­ниченно генерирует дислокационные петли в разных атомных плоскостях. На рис. 15.4 в г. ц. к. решетке в плоскости скольжения {111} исходная дислока­ция DD' закреплена в узлах D и D', в которых сходятся по три дислока­ции. Дислокации AD, DB, CD' и D'E, не лежащие в плоскости легкого сколь­жения,— неподвижные или малоподвижные. Точки D и D' принадлежат одновременно им и легко скользящей дислокации DaD'. Поэтому под дейст­вием приложенной силы дислокация DaD' перемещается не параллельно са­мой себе, а выгибается в полуокружность и далее закручивается вокруг то­чек D и D'. Если векторы Бюргерса неподвижных дислокаций, сходящихся о точках D и D', имеют винтовую компоненту по отношению к плоскости {111}, то закручивающиеся участки дислокации DaD' скользят по винтовой поверхности. Совершив один оборот, участок скользящей дислокации под­нимается или опускается с одного горизонта на другой. На рис. 15.4 закру­чивающиеся участки в результате полного оборота перемещаются вверх на одно межатомное расстояние. Соприкоснувшись позади источника, две сим­метричные части спирали, имеющие противоположный знак. аннигилируют. В результате этого образуется замкнутая петля, которая может неограни­ченно распространяться, и участок дислокации, выпрямляющийся в отрезок DbD' (аналогично работе плоского источника, см. рис. 15.3, б). Особенность конического источника — то, что стартовое положение дислокации в каждый новый цикл оказывается на ином горизонте, чем в предыдущий цикл (DbD' вместо DaD'). Соответственно каждая новая петля распространяется в пло­скости, которая отстоит от плоскости предыдущей петли на одно межатом­ное расстояние (это расстояние показано штриховкой на рис. 15.4).

О том, какие дислокации могут размножаться по механизму Франка—Рида, имеются разные предположения. Первоначально считалось, что основную роль в размножении дислокаций иг­рают отрезки пространственных дислокационных сеток, концы которых закреплены, так как они связаны с неподвижными или малоподвижными дислокациями в сетках. Такой элемент сетки DD' показан на рис. 15.4. Позднее были получены эксперимен­тальные данные, поставившие под сомнение ведущую роль эле­ментов дислокационных сеток в размножении дислокаций при пластической деформации.

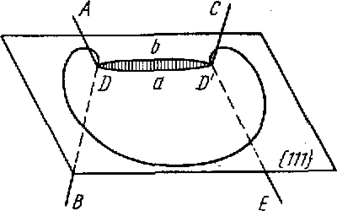
Рис. 15.4. Пространственный (кониче­ский) источник Франка — Рида

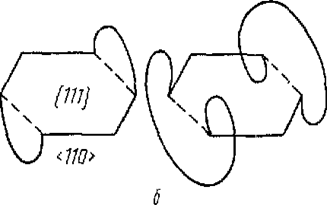
Другой вероятный источник размножения дислокаций–R-дислокация, возникающая в результате захлопывания вакансионных дисков. На­пример, если в плоскости AВС стандартного тетраэдра при захлопывании диска вакансий возникает дефект упа­ковки, то образуется сидячая дис­локация Франка с вектором Бюргерса dD. Взаимодействуя с частичной дислокацией Шокли Ad, она образует R-дислокацию с вектором Бюргерса AD, так как Ad+dD=AD. Дефект упа­ковки, существующий до образования R-дислокации в плоско­сти AВС, чаще всего имеет вид шестиугольника, стороны ко­торого параллельны АВ, ВС и АС (рис. 15.5, а).

Соответственно и R-дислокация будет состоять из шести сег­ментов, параллельных этим трем направлениям (рис. 15.5). Пло­скостью скольжения ^-дислокации может быть только такая плоскость {111}, которая содержит и линию дислокации, и ее вектор Бюргерса. Если образовалась призматическая R-дислокация с вектором Бюргерса AD, то только сегменты шести­угольника, параллельные АВ и АС, могут участвовать в сколь­жении (каждый из них совместно с вектором Бюргерса AD ле­жит в одной из плоскостей {111} —ADB или ADC). Кроме того, в возможных плоскостях скольжения сегментов R-дислокации действуют разные касательные напряжения.

Таким образом, одни сегменты R-дислокации вообще не мо­гут скользить, а другие малоподвижны. Поэтому сегмент, нахо­дящийся в плоскости легкого скольжения, оказывается закреп­ленным по концам и может действовать как источник Франка— Рида (см. рис. 15.5).

Источник Франка—Рида может образоваться также при двойном поперечном скольжении. Допустим, что дислокацион­ная петля распространялась в плоскости (111) и была останов­лена каким-то препятствием. Тогда она переходит в плоскость поперечного скольжения (111), где хотя и действуют меньшие касательные напряжения, но нет препятствий, Выйдя из района препятствия, дислокация будет стремиться возвратиться в пло­скость (111), где действуют большие касательные напряжения.

 

Рис. 15.5 Шестиугольные петли дислокаций с дефектами упаковки внутри них, образовавшиеся о закаленном алюминии при захлопывании дисков вакансий (а), и отрезки призматической петли, действующие пик источники Франка—Рида (б)

Если в плоскости поперечного скольжения (111) из-за низкого касательного напряжения оставшиеся здесь участки дислокации окажутся малоподвижными, то петля, легко распространяющая­ся в плоскости (111), будет за­креплена по концам и станет ис­точником Франка—Рида.

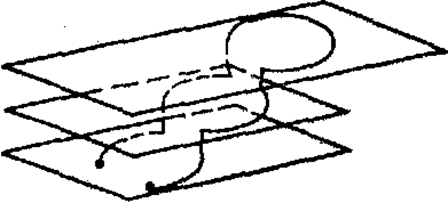
Рис. 15.6. Размножение дислокаций при множественном поперечном скольжении

Множественное поперечное скольжение, которое приводит к образованию дислокационной линии большой протяженности, переходящей из одной парал­лельной плоскости в другую, и к работе источников Франка-Рида в этих плоскостям, является эффективным механизмом размножения дислокаций (рис. 15.6).

Контрольные вопросы

1. Объясните образование винтовой дислокации на фронте кристаллизации.

2. Объясните, что служит подложкой для зарождения кристалла.

3. Объясните, какие дислокации называют структурными или дислокациями несоответст­вия.

4. Объясните образование дислокаций в полностью затвердевшем металле в непосредст­венной близости от фронта кристаллизации и вдали от него.

5. Объясните возникновение дислокации при концентрации напряжений в отдельных уча­стках кристаллов (около включений, трещин, границ двойников и т.д.).

6. Объясните, что называют дислокационной сеткой.

7. Объясните механизм размножения дислокаций в процессе пластической деформации.

8. Объясните, что является зоной при размножении дислокаций при пластической дефор­мации.

9. Объясните, как называется напряжение, требующееся для выгибания линии дислокации в полуок­ружность.

10. Объясните, как ведет себя замкнутая дислокационная петля.

11. Объясните, почему при напряжении, действующем в одном направлении, сначала спи­ральные участки дислокации, а затем замкнутая петля распространяются во все стороны, в том числе и в направлении прямо противоположном приложенному на­пряжению.

12. Объясните источник размножения дислокаций – R дислокация, возникающих в резуль­тате захлопывания вакансионных дисков.

13. Объясните образование источника Франка-Рида при двойном поперечном скольже­нии.

Дата добавления: 2014-01-07