Численное решение нелинейного уравнения

Решение уравнений средствами Mathcad

Способы решения уравнений. Поиск начального приближения. Графическое решение уравнений. Поиск корней Полина с использованием функции polyroots

Тема: Численное и символьное решение уравнений. Корни полинома

Лекция 3

Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Однако такие уравнения могут решаться численными методами с заданной точностью (не более значения заданного системной переменной TOL).

Для простейших уравнений вида f (x) = 0 решение в Mathcad находится с помощью функции root (Рисунок 5).

root(f (х 1, x 2, …), х 1, a, b) – Возвращает значение х 1, принадлежащее отрезку [ a, b ], при котором выражение или функция f (х) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.

Аргументы:

f (х 1, x 2, …) -функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.

х 1 -- имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.

a, b – необязательны, если используются, то должны быть вещественными числами, причем a < b.

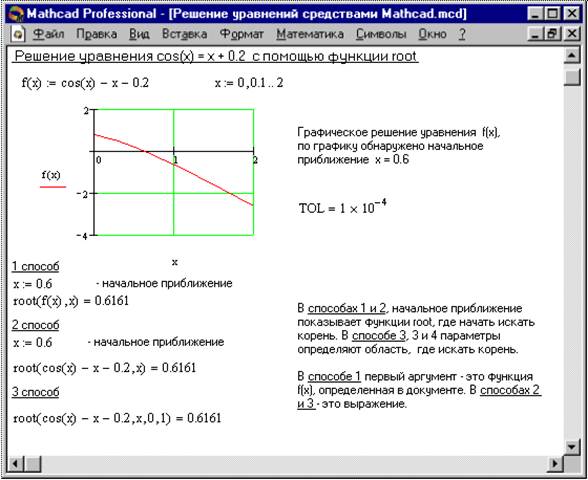
Рисунок 4. Решение уравнений средствами Mathcad

Приближенные значения корней (начальные приближения) могут быть:

1. Известны из физического смысла задачи.

2. Известны из решения аналогичной задачи при других исходных данных.

3. Найдены графическим способом.

Наиболее распространен графический способ определения начальных приближений. Принимая во внимание, что действительные корни уравнения f (x) = 0 - это точки пересечения графика функции f (x) с осью абсцисс, достаточно построить график функции f (x) и отметить точки пересечения f (x) с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение f (x) = 0 равносильным ему уравнением: 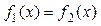,где функции f ₁(x) и f ₂(x) - более простые, чем функция f (x). Тогда, построив графики функций у = f ₁(x) и у = f ₂(x), искомые корни получим как абсциссы точек пересечения этих графиков.

Пример. Графически отделить корни уравнения: x lg x = 1. Это уравнение удобно переписать в виде равенства: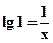

Отсюда ясно, что корни уравнения могут быть найдены как абсциссы точек пересечения логарифмической кривой y = lg x и гиперболы y = 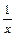. Построив эти кривые, приближенно найдем единственный корень 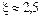уравнения или определим его содержащий отрезок [2, 3].

Дата добавления: 2014-01-07