Случайные погрешности

Формально абсолютную погрешность измерения физической величины Х будем представлять в виде суммы двух составляющих D Х = D_с + , где - случайная составляющая относительной погрешности 120. Графическая интерпретация сказанного приведена на рисунке 2.1.

Случайная погрешность здесь определяется разностью между результатами однократного наблюдения Х_i и математическим ожиданием результатов МХ:

D= Х_i – М(Х) (2.5)

  Р(x)  

Х

Рис. 2.1. Слагаемые абсолютной погрешности i -го наблюдения величины X

Случайные величины Х_i и их погрешности D° могут быть описаны с помощью интегральной и дифференциальной функции распределения, графики которых изображены на 2.2

Рис. 2.2. Интегральная (а) и дифференциальная (б) функция распределения

Интегральная функция распределения результатов наблюдений определяет вероятность (Р) нахождения результатов наблюдения Х_i в диапазоне от - ¥ до некоторого текущего значения Х:

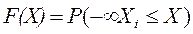. (2.6)

Дифференциальная функция (плотность вероятностей) чаще применяется в метрологии для описания случайных погрешностей. Взаимосвязь этих двух функций можно представить в виде:

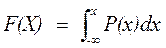. (2.7)

Для характеристики случайной погрешности необходимо задавать не только значение погрешности (доверительный интервал), но и значение вероятности. Знание доверительной вероятности позволяет оценить степень надежности полученного результата.

На рис. 2.3, а показан графический метод определения вероятности попадания результатов наблюдений в заданный интервал X₁-X₂ по интегральной функции распределения:

Р(X₁ < X £ X₂) = F(X₂) – F(X₁). (2.8)

На рис. 2.3б показано то же самое, но с помощью распределения P(X):

. (2.9)

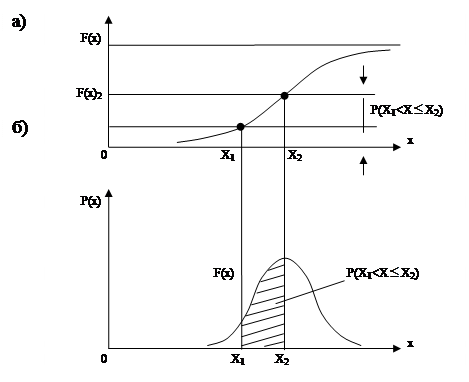Рис. 2.3. Графический метод определения вероятности

показаний результатов измерений

Приведенные графические пояснения понятий доверительного интервала и доверительной вероятности в дальнейшем помогут в использовании таблиц, связывающих значения этих величин между собой, при обработке результатов наблюдений.

Кривая распределения Р (Х) рис. 2.3б соответствует нормальному закону распределения погрешностей (НЗР). НЗР называют ещё законом распределения Гаусса. Этот - закон один из наиболее распространенных законов распределения погрешностей (это подтверждается центральной предельной теоремой теории вероятности) и широко применяется при оценке результатов измерений.

При НЗР дифференциальная функция имеет вид

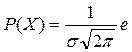
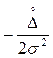^. (2,10)

Функция распределения нормальной случайной величины определяется выражением:

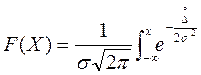. (2.11)

При НРЗ дифференциальная функция имеет графический вид, показанный на рис.2.4.

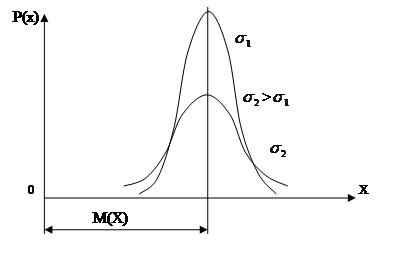Рис.2.4. Дифференциальные функции НЗР

Из рис. 2.4 и уравнения 2.4 следуют выводы:

1) плотность вероятностей имеет максимум при Х=М(Х)

2) с ростом погрешности = Х_i – М (Х), независимо от знака (функция четная), плотность вероятности стремится к нулю;

3) с увеличением среднего квадратического отклонения (d) вероятность больших отклонений увеличивается, т.е. результаты наблюдений рассеиваются в более широком диапазоне.

Из рис. 2.4 видно, что кривая распределения меняется в зависимости от среднего квадратического отклонения (СКО). Если выразить погрешность в долях от СКО (d), то получим кривую нормированного НЗР с аргументом

T = /d. (2.12)

Эта кривая описывается выражением

; (2.13)

оно имеет место при условии, если

.

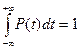При этом интегральная функция нормального нормированного распределения имеет вид:

, (2.14)

где аргумент Z так же, как и в (2.12), определяется отношением:

Z = /d. (2.15)

Вид функции Ф(Z) показан на рисунке 2.5, а значения Ф(Z) в виде фрагментов из специальной таблицы – в табл. 2.1.

Рис. 2.5. Интегральная функция нормированного

нормального распределения

В качестве примеров практического использования данных таблицы 2.1 рассчитаем значения доверительной вероятности Р для наиболее распространенных значений T = /d: t = 1; t = 2; t = 3, т.е. для погрешностей, равных ±d; ±2d; ±3d, по формуле:

P ₁ = Ф(Z = 1) – Ф(Z = -1) = 0,8413 – 0,1587 = 0.6826,

P ₁ = Ф(Z = 2) – Ф(Z = -2) = 0,9772– 0,0228 = 0.9544,

P ₁ = Ф(Z = 3) – Ф(Z = -3) = 0,99865 – 0.00135 = 0.9973.

Таблица 2.1

Интегральная функция нормированного нормального распределения:

.

Z	0,08	0,06	0,04	0,02	0,00
-3,5	0,00017	0,00019	0,00020	0,00022	0,00023
-3,0	0,00104	0,00111	0,00118	0,00126	0,00135
-2,5	0,0049	0,0052	0,0055	0,0059	0,0062
-2,0	0,0188	0,0197	0,0207	0,0217	0,0228
-1,5	0,0571	0,0594	0,0618	0,0643	0,0668
-1,0	0,1401	0,1446	0,1492	0,1539	0,1587
-0,5	0,2810	0,2877	0,2946	0,3015	0,3085
-0,0	0,4681	0,4761	0,4840	0,4920	0,5000
+0,0	0,5319	0,5239	0,5160	0,5080	0,5000
+0,5	0,7190	0,7123	0,7054	0,6985	0,6915
+1,0	0,8599	0,8554	0,8505	0,8461	0,8413
+1,5	0,9429	0,9406	0,9382	0,9257	0,9332
+2,0	0,9812	0,9803	0,9793	0,9783	0,9773
+2,5	0,9951	0,9948	0,9945	0,9941	0,9938
+3,0	0, 99896	0,99889	0,99882	0,99874	0,99865
+3,5	0,99983	0,99981	0,99980	0,99978	0,99977

Эти же значения Р можно получить, используя выражение:

Р = 2Ф(Z) – 1. (2.16)

Например: Р ₁ = 2Ф(Z = 1) – 1 = 2*0,8413 – 1 = 0,6826.

Если для расчета Р использовать нормированную функцию Лапласа, то Р находим по выражению

Р =2Ф₀(Z). (2.17)

Эта функция определяется интегралом от нормальной плотности вероятности в пределах 0... Z:

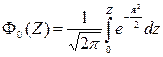. (2.18)
Значения интеграла Ф₀(Z) приведены в таблице 2.2 при t = Z в пределах от 0 до 5.

Таблица 2.2

Таблица значений интеграла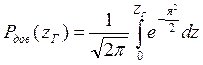

z г	Р дов(z г)	z г	Р дов(z г)	z г	Р дов(z г)	z г	Р дов(zг)
0,00 0,02 0,04 0,06 0,08 0,10 0,12 0,14 0,16 0,18 0,20 0,22 0,24 0,26 0,28 0,30 0,32 0,33 0,35 0,37 0,39 0,41 0,43 0,45 0,47 0,49 0,51 0,53 0,57 0,59 0,61 0,63 0,65	0,0000 0,0080 0,0160 0,0239 0,0319 0,0398 0,0478 0,0557 0,0636 0,0714 0,0793 0,0871 0,0948 0,1026 0,1103 0,1179 0,1255 0,1293 0,1368 0,1443 0,1517 0,1591 0,1664 0,1736 0,1808 0,1879 0,1950 0,2019 0,2157 0,2224 0,2291 0,2357 0,2422	0,66 0,68 0,70 0,72 0,74 0,76 0,78 0,80 0,82 0,84 0,86 0,88 0,90 0,92 0,94 0,96 0,98 0,99 1,01 1,03 1,05 1,07 1,09 1,11 1,13 1,15 1,17 1,19 1,23 1,25 1,27 1,29 1,31	0,2454 0,2517 0,2580 0,2642 0,2703 0,2764 0,2823 0,2881 0,2939 0,2995 0,3051 0,3106 0,3159 0,3212 0,3264 0,3315 0,3365 0,3389 0,3438 0,3485 0,3531 0,3577 0,3621 0,3665 0,3708 0,3749 0,3790 0,3830 0,3907 0,3944 0,3980 0,4015 0,4049	1,32 1,34 1,36 1, 38 1,40 1,42 1,44 1,46 1,48 1,50 1,52 1,54 1,56 1,58 1,60 1,62 1,64 1,66 1,68 1,70 1,72 1,74 1,76 1,78 1,80 1,82 1,84 1,86 1,90 1,92 1,94 1,96 1,98	0,4066 0,4099 0,4131 0,4162 0,4192 0,4222 0,4251 0,4279 0,4306 0,4332 0,4357 0,4382 0,4406 0,4429 0,4452 0,4474 0,4495 0,4515 0,4535 0,4554 0,4573 0,4591 0,4608 0,4625 0,4641 0,4656 0,4671 0,4688 0,4713 0,4726 0,4728 0,4750 0,4761	2,00 2,04 2,08 2,12 2,16 2,20 2,24 2,28 2,32 2,36 2,40 2,44 2,48 2,52 2,56 2,60 2,64 2,68 2,72 2,76 2,80 2,84 2,88 2,92 2,96 3,00 3,40 3,80 5,00	0,4772 0,4793 0,4812 0,4830 0,4846 0,4831 0,4875 0,4887 0,4898 0,4909 0,4918 0,4927 0,4934 0,4941 0,4948 0,4953 0,4959 0,4963 0,4967 0,4971 0,4974 0,4977 0, 4980 0,4982 0,4985 0,49865 0,49966 0,49982 0,5

Все вышеизложенное относительно Р и границ случайных погрешностей, указанных в долях СКО (d), справедливо при заранее известном d и НЗР, т.е. при предельном СКО, когда n à ¥ (большая выборка наблюдений).

На практике имеют место незначительные выборки порядка n = 20...30 наблюдений. При этом готовое значение d неизвестно, и требуется по ограниченному количеству наблюдений рассчитать (оценить) эмпирическое значение СКО, которое в дальнейшем будем обозначать как (оценка среднего квадратического отклонения результатов наблюдений) и находить из выражения

, (2.19)

где 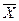– среднее арифметическое результатов n наблюдений.

Оценка может быть использована при необходимости характеризовать точность применяемого метода измерения.

Для оценки же погрешности значения Х, полученного в результате обработки измерений, следует пользоваться (оценкой среднего квадратического отклонения результатов измерения), которая определяется из уравнения

,

где 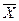– результат измерения (оценка математического ожидания).

Учитывая ограниченное число наблюдений, можно определить с заданной доверительной вероятностью Р доверительные границы для истинного значения измеряемой величины с помощью распределения Стьюдента t_SГ, при этом доверительная граница случайной погрешности будет найдена по выражению:

, (2.20)

где t_SГ находим по таблице 2.3.

Значение коэффициента t_SГ для случайной величины t_S, имеющей распределение Стьюдента с n -1 степенями свободы, определяется из условия P [| t_S |< t_SГ] = P _дов

Распределения Стьюдента в зависимости от n и P

Таблица 2,3

n -1	P = 0.95	P = 0.99	n -1	P = 0.95	P = 0.99
	12,706 4,303 3,182 2,776 2,571 2,447 2,365 2,306 2,262 2,228	63,657 9,925 5,841 4,604 4,032 3,707 2,998 3,355 3,250 3,169		2,179 2,145 2,120 2,101 2,086 2,074 2,064 2,056 2,048 2,043 1,960	3,055 2,997 2,921 2,678 2,845 2,819 2,797 2,779 2,763 2,750 2,576

Дата добавления: 2014-01-07