Камеральные работы

1. Находим практическую (измеренную) сумму внутренних углов полигона

Σβ_изм = β₁+ β₂+ …+ β_n

2. Определяем теоретическую сумму внутренних углов полигона

Σβ_теор = 180°·(n-2)

3. Находим угловую невязку – разность суммы измеренных и теоретической суммы углов полигона.

f_β = Σβ_изм - Σβ_теор

4. Вычисляем допустимую невязку в углах

f_{β доп} = ±1’√n

5. Если f_β не превышает f_{β доп},то угловая невязка распределяется по измеренным углам полигона с обратным знаком. Большие поправки вводят в углы с короткими сторонами.

δ_β = - f_β /n

Контроль: сумма поправок должна быть равна невязке с обратным знаком

Σδ_β = - f_β

6. Алгебраически складывая вычисленные поправки с измеренными углами, получают исправленные углы

β_испр= β_изм + δ_β

Контроль: Σ β_испр= β_теор

7. По известному дирекционному углу начальной стороны и значениям исправленных внутренних углов полигона последовательно вычисляем дирекционные углы всех сторон по формуле:

_n = _n-1 +180° - β_n.

Контроль: повторное получение дирекционного угла начальной стороны.

8. По найденным значениям дирекционных углов сторон находим румбы.

9. Вычисляем приращения координат по формулам прямой геодезической задачи

Δх = d·cos r;

Δу = d·sin r

Знаки приращений координат определяем с учетом четверти по дирекционному углу стороны

10. Находим линейную невязку f_х и f_у как разность между приращениями

11. По вычисленным линейным невязкам f_х и f_у находим абсолютную невязку хода: f_абс = √fx² + fy²

12. Находим относительную невязку хода:

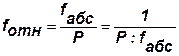
Контроль: f_отн < f _{отн доп}

13. Если относительная невязка допустима, то производим увязку приращений координат. Невязки f_х и f_у распределяются по вычисленным приращениям координат пропорционально длинам сторон с обратным знаком.

Σδ_х = - f_х /n

Σδ_у = - f_у /n

14. По вычисленным приращениям координат и поправкам находят исправленные приращения координат

Δх_испр= Δх + δ_х

Δу_испр= Δу + δ_у

Контроль: ΣΔх_испр= 0

ΣΔу_испр= 0

15. По исправленным приращениям координат и координатам начальной точки вычисляют координаты всех точек полигона:

х_n+1 = х_n + Δх_испр

у_n+1 = у_n + Δу_испр

Контроль: получение координат начальной точки теодолитного хода

Дата добавления: 2014-01-07