Понятие о гидродинамическом подобии и критериях подобия

Большинство физических явлений не поддаются математическому описанию и пост-роению математической модели. Поэтому в гидромеханике большая роль отводится экс-периментальным методам исследования на геометрически подобных моделях реальных объектов выполненных в определенном масштабе.

Основой моделирования гидромеханических процессов является теория подобия.

Подобными называются системы в которых протекают процессы одинаковой приро-ды и имеющие равные величины.

Применяя теорию подобия можно по характеристикам одного объекта изучить хара-ктеристики другого, подобного первому, методом соответствующих преобразований.

Гидродинамическое подобие условно состоит из 3-х видов: геометрического, кине-матического и динамического.

4.1.3.1 Геометрическое подобие представляет собой пропорциональность одинако-вых линейных размеров модели и натурного объекта.

Отношение подобных размеров двух подобных объектов называется линейным мас-штабом:

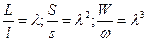
Где,

L,l - длина натурного объекта и модели, м;

S,s - площадь натурного объекта и модели, м²;

W,ω - объем натурного объекта и модели, м³;

λ - линейный масштаб моделирования.

4.1.3.2 Кинематическое подобие представляет собой пропорциональность скорос-тей потока в одинаковых точках модели и натурного объекта при геометрическом подо-бии линии тока жидкости:

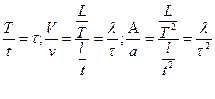
Где,

T,t - реальное время процесса и время проведенных исследований, с;

τ- масштаб времени;

V, v- скорость реального потока и экспериментального, м/с;

A,a - ускорение реального потока и экспериментального, м/с².

4.1.3.3 Динамическое подобие представляет собой пропорциональность соответс-твующих сил, которые возникают в кинематически подобных потоках жидкости

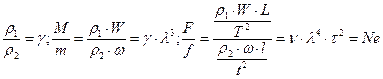
Где,

F,f - силы действующие на объекты, Н

Отношение возникающих сил вызванных подобными потоками является математи-ческим выражением основного закона динамического подобия и носит название критерия Ньютона (Ne).

Соблюдение пропорциональности сил давления, сил веса, сил трения, сил поверх-носного натяжения, сжатия и других физических параметров в реальном потоке жидкости на реальном объекте и в эксперименте на модели определяет полное гидромеханическое подобие.

На практике соблюсти полное подобие почти невозможно, поэтому стараются выдержать пропорциональность только основных сил действующих на реальные тела и на модели:

1 Если в потоке основными силами являются силы давления, то подобие соблюдает-ся числом Эйлера:

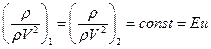
2 Если в потоке основными силами являются силы трения, то подобие соблюдается числом Рейнольдса:

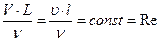
3 Если в потоке основными силами являются силы веса, то подобие соблюдается числом Фруда:

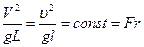
4 Если поток сжимаемый, то подобие соблюдается числом Маха:

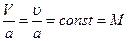
5 Если в потоке основными силами являются силы поверхносного натяжения, то подобие оценивается числом Вебера- (We)

6 Если в потоке основными силами являются силы инерции в условиях нестационар-ности течения потока, то подобие оценивается числом Струхаля- (St).

Таким образом, в подобных потоках должно быть равенство безразмерных коэффи-циентов и чисел:

· коэффициентов Кориолиса (α);

· коэффициентов сопротивления (ζ);

· коэффициентов Дарси (λ);

· числа Эйлера(коэффициента давления) (Eu);

· чисел Ньютона (Ne);

· чисел Рейнольдса (Re).

Дата добавления: 2014-01-07