Математическая модель операции

Для применения количественных методов исследования требуется построить математическую модель операции. При построении модели операция, как правило, схематизируется, и схема операции описывается с помощью того или иного математического аппарата. Модель операции – это приближенное описание операции с помощью математического аппарата (различного рода функций, уравнений, систем уравнений и неравенств и т.д.). Составление модели операции требует понимания сущности описываемого явления и знания математического аппарата.

Краеугольным камнем исследования операций является математическое моделирование. Хотя данные, полученные в процессе исследования математических моделей, являются основой для принятия решений, окончательный выбор обычно делается с учетом многих других "нематериальных" (не имеющих числового выражения) факторов (таких как человеческое поведение), которые невозможно отобразить в математических моделях.

В моделях ИО понятие "оптимальности" решений определяется с учетом соответствия этого решения множеству ограничений. Это означает, что качество конечного решения, сделанного на основе решения задачи, зависит от адекватности представления моделью реальной ситуации, которую она формально описывает посредством ограничений. Таким образом, конкретное оптимальное решение является наилучшим только для этой модели. Чем модель лучше отображает реальную ситуацию, тем ближе решение этой задачи к оптимальному.

Можно выделить следующие основные этапы исследования операций:

1) наблюдение явления и сбор исходных данных;

2) постановка задачи;

3) построение математической модели;

4) расчёт модели;

5) тестирование модели и анализ выходных данных. Если полученные данные не удовлетворяют исследователя, то следует вернуться на этап 3, т.е. предложить для решения задачи другую математическую модель; либо вернуться на этап 2,т.е. поставить задачу более корректно;

6) применение результатов исследований.

Т.о., операционное исследование является итерационным процессом, каждый следующий шаг которого приближает исследователя к решению стоящей перед ним проблемы. В центре операционного исследования находятся построение и расчёт математической модели.

Математическая модель – это система математических соотношений, приближённо, в абстрактной форме описывающих изучаемый процесс или систему.

Экономико-математическая модель – это математическая модель, предназначенная для исследования экономической проблемы.

В настоящее время математические модели применяются для анализа, прогнозирования и выбора оптимальных решений в различных областях экономики. Это планирование и эффективное управление производством, управление трудовыми ресурсами, управление запасами, распределение ресурсов, планировка и размещение объектов, распределение инвестиций и т.п.

5. Классификация и принципы построения математических моделей

Можно выделить следующие основные этапы построения математической модели.

1) Определение цели.

2) Определение параметров модели, т.е. заранее известных фиксированных факторов, на значения которых исследователь не влияет (постоянные факторы).

3) Формирование управляющих переменных (зависимые факторы или элементы решения), изменяя значения которых можно приближаться к поставленной цели. Значения управляющих переменных являются решениями задачи.

4) Определение области допустимых решений, т.е. тех ограничений, которым должны удовлетворять управляющие переменные.

5) Выявление неизвестных факторов, т.е. величин которые могут изменяться случайным или неопределённым образом.

6) Выражение цели через управляющие переменные, параметры и неизвестные факторы, т.е. формирование целевой функции, называемой также критерием эффективности или критерием оптимальности задачи.

Введём условные обозначения:

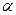- параметры модели;

x – управляющие переменные или решения;

X – область допустимых решений;

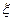- случайные или неопределённые факторы;

f – целевая функция или критерий эффективности.

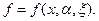
В соответствии с введёнными терминами математическая модель задачи имеет следующий вид:

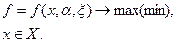
Решить задачу – это значит найти такое оптимальное решение 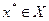, чтобы при данных фиксированных параметрах 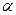и с учётом неизвестных факторов 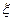значение критерия эффективности f было максимальным (минимальным). Для решения такой задачиприменяются методы математического программирования.

Перечислим некоторые основные принципы построения математической модели.

1. Необходимо соизмерять точность и подробность модели, во-первых с точностью тех исходных данных, которыми располагает исследователь, и

во-вторых, с теми результатами, которые требуется получить.

2. Математическая модель должна отражать существенные черты исследуемого явления и при этом не должна его сильно упрощать.

3. Математическая модель не может быть полностью адекватна реальному явлению, поэтому для его исследования лучше использовать несколько моделей, для построения которых применены разные математические методы. Если при этом получаются сходные результаты, то исследование заканчивается. Если результаты сильно различаются, то следует пересмотреть постановку задачи.

4. Любая сложная система всегда подвергается малым внешним и внутренним воздействиям, следовательно, математическая модель должна быть устойчивой, т.е. сохранять свои свойства и структуру при этих воздействиях.

По числу критериев эффективности математические модели делятся на однокритериальные и многокритериальные. Многокритериальные математические модели содержат два и более критерия.

По учёту неизвестных факторов математические модели делятся на детерминированные, стохастические и модели с элементами неопределённости.

В детерминированных моделях неизвестные факторы не учитываются. Несмотря на кажущуюся простоту этих моделей, к ним сводятся многие практические задачи, в том числе большинство экономических задач. По виду целевой функции и ограничений детерминированные модели делятся на линейные, нелинейные, динамические и графические.

В линейных моделях целевая функция и ограничения линейны по управляющим переменным. Построение и расчёт линейных моделей являются наиболее развитым разделом математического моделирования, поэтому часто к ним стараются свести и другие задачи либо на этапе постановки, либо в процессе решения. Большое число экономических задач сводится к линейным математическим моделям. Под линейным программированием понимается получение оптимального плана – решения в задачах с линейной структурой.

(В исследовании операций нет единого общего метода решения всех математических моделей, которые встречаются на практике. Вместо этого выбор метода решения диктуют тип и сложность исследуемой математической модели. Наиболее известными и эффективными методами ИО являются методы линейного программирования, когда целевая функция и все ограничения являются линейными функциями. Для решения математических моделей других типов предназначены методы целочисленного программирования (если все переменные должны принимать только целочисленные значения), динамического программирования (где исходную задачу можно разбить на меньшие подзадачи) и нелинейного программирования (когда целевая функция и/или ограничения являются нелинейными функциями). Перечисленные методы составляют только часть из большого количества самых разнообразных доступных методов исследования операций.)

6. Постановка задачи линейного программирования.

В общем виде задача линейного программирования ставится следующим образом.

Максимизировать (минимизировать) функцию

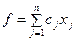
(1)

при ограничениях

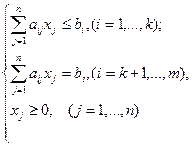(2)

где 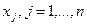- управляющие переменные или решения задачи,

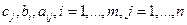- параметры,

f – целевая функция или критерий эффективности.

Функция (1) – линейная, ограничения (2) – тоже линейные. Задача содержит n переменных и m ограничений.

Определение 3. Совокупность чисел 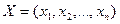, удовлетворяющих ограничениям задачи, называется допустимым решением (или планом).

Определение 4. План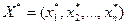, при котором целевая функция принимает максимальное (минимальное) значение, называется оптимальным.

Определение 5. Непустое множество планов задачи линейного программирования называется многогранником решений, а всякая угловая точка многогранника решений – вершиной.

Решить задачу линейного программирования – значит найти значения управляющих переменных 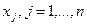, удовлетворяющих ограничениям (2), при которых целевая функция (1) принимает максимальное или минимальное значение.

Если, при условии, что все переменные 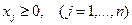неотрицательны, система ограничений (2) состоит лишь из одних неравенств, то такая задача линейного программирования называется стандартной, если система ограничений состоит из одних уравнений, то задача называется канонической (основной).

Любая задача линейного программирования может быть сведена к канонической, стандартной или общей задаче.

Справедлива теорема.

Теорема 1. Любому решению 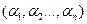неравенства

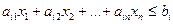(3)

соответствует определенное решение 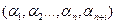уравнения

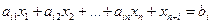(4)

в котором

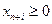(5)

и, наоборот, каждому решению 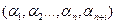уравнения (4) и неравенства (5) соответствует определенное решение 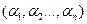неравенства (3).

Замечание. Ограничения-неравенства исходной задачи линейного программирования, имеющие вид «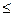», можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида «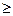» - в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной.

Приведём пример экономической задачи, сводящейся к линейной модели.

Пример 1. Предприятие производит изделия трёх видов, поставляет их заказчикам и реализует на рынке. Заказчикам требуется 1000 изделий первого вида, 2000 изделий второго вида и 2500 изделий третьего вида.

Условия спроса на рынке ограничивают число изделий первого вида 2000 единицами, второго – 3000 и третьего – 5000 единицами.

Для изготовления изделий используется 4 типа ресурсов. Количество ресурсов, потребляемых для производства одного изделия, общее количество ресурсов и прибыль от реализации одного изделия каждого вида заданы в таблице.

Тип ресурсов	Вид изделий	Всего ресурсов
	1 000		1 000	25 000 30 000 20 000 40 000
Прибыль

Как организовать производство, чтобы:

1) обеспечить заказчиков;

2) не допустить затоваривания;

3) получить максимальную прибыль?

Построение математической модели.

1) Цель – получение максимальной прибыли.

2) Параметрами являются все числовые данные, приведённые в условии задачи.

3) Управляющие переменные:

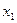- число изделий первого вида,

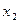- число изделий второго вида,

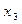- число изделий третьего вида.

4) Ограничения: обеспечить заказчиков, не превысить запас ресурсов, не допустить затоваривания рынка.

В соответствии с этими ограничениями выпишем область допустимых решений задачи:

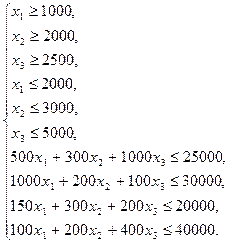
Первые три неравенства в системе соответствуют спросу заказчиков; неравенства с четвёртого по шестое формализуют спрос на рынке; последние четыре неравенства соответствуют ограничениям по ресурсам.

5) Целевая функция задачи имеет вид

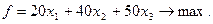
Пример 2. При составлении суточного рациона кормления скота используют сено и силос. Рацион должен обладать определённой питательностью и содержать белка не менее 1 кг, кальция не менее 100 г и фосфора не менее 80 г. При этом количество питательного рациона должно быть не менее 60 кг. Содержание питательных компонентов в 1 кг сена и силоса приведено в таблице. В ней указана также стоимость единицы того или иного корма.

Название ингридиента	Норма (г)	Содержание ингридиента в 1 кг корма (г/кг)
Сено	Силос
Белок Кальций Фосфор		1,25	2,5
Стоимость ед. корма (ден.ед.)

Требуется определить оптимальный суточный рацион кормления животных, обеспечивающий минимальную стоимость корма.

Построение математической модели.

Обозначим через 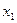и 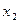количества килограммов сена и силоса соответственно, составляющих рацион на одно животное в течение суток. Тогда условие задачи означает, что необходимо минимизировать функцию стоимости

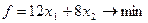
при следующих ограничениях:

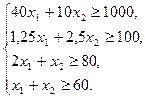
Теорема 2. Если задача линейного программирования имеет оптимальный план, то максимальное (минимальное) значение целевая функция задачи принимает в одной из вершин многогранника решений. Если такое значение целевая функция принимает более чем в одной вершине, то она принимает его во всякой точке, являющейся выпуклой линейной комбинацией этих вершин.

Практически все методы ИО не позволяют получить решение в замкнутой (в виде формул) форме. Напротив, они порождают вычислительные алгоритмы, которые являются итерационными по своей природе. Это означает, что задача решается последовательно (итерационно), когда на каждом шаге (итерации) получаем решения, постепенно сходящиеся к оптимальному. Итерационная природа алгоритмов обычно приводит к объемным однотипным вычислениям. В этом и заключается причина того, что эти алгоритмы разрабатываются, в основном, для реализации с помощью вычислительной техники. Некоторые математические модели могут быть такими сложными, что их невозможно решить никакими доступными методами оптимизации. В этом случае остается только эвристический подход: поиск подходящего "хорошего" решения вместо оптимального. Эвристический подход предполагает наличие эмпирических правил, в соответствии с которыми ведется поиск подходящего решения.

Несмотря на впечатляющие достижения математического моделирования, многие реальные ситуации невозможно адекватно представить с помощью соответствующих математических моделей. Часто в этом "виновата" определенная "жесткость" математики как языка описания и представления событий и явлений. Но даже если существует возможность формализовать рассматриваемую жизненную ситуацию посредством построения математической модели, полученная на ее основе задача оптимизации может быть слишком сложной для современных алгоритмов решения задач этого класса.

Альтернативой математическому моделированию сложных систем может служить имитационное моделирование. Различие между математической и имитационной моделями заключается в том, что в последней отношение между "входом" и "выходом" может быть явно не задано. Вместо явного математического описания взаимоотношения между входными и выходными переменными математической модели, при имитационном моделировании реальная система разбивается на ряд достаточно малых (в функциональном отношении) элементов или модулей. Затем поведение исходной системы имитируется как поведение совокупности этих элементов, определенным образом связанных (путем установки соответствующих взаимосвязей) в единое целое. Вычислительная реализация такой модели начинается с входного элемента, далее проходит по всем элементам, пока не будет достигнут выходной элемент. Имитационные модели значительно гибче в представлении реальных систем, чем их математические "конкуренты". Причина такой гибкости заключается в том, что при имитационном моделировании исходная система рассматривается на элементарном уровне, а математические модели стремятся описать системы на глобальном уровне. За гибкость имитационных моделей приходится платить высокими требованиями к потребляемым временным и вычислительным ресурсам. Поэтому реализация некоторых имитационных моделей даже на современных быстрых и высокопроизводительных компьютерах может быть очень медленной.

Дата добавления: 2014-01-07