Спецификация модели

Линейная модель множественной регрессии

Эконометрика – это наука, изучающая количественные взаимосвязи экономических показателей на основе использования аппарата теории вероятностей и математической статистики.

Эта наука возникла в результате взаимодействия и объединения экономической теории, статистики (как экономической, так и математической) и других разделов математики. Методы эконометрики позволяют выявлять новые, ранее не известные связи между экономическими показателями, а также уточнять или отвергать гипотезы о существовании таких связей.

Эконометрическая модель, таким образом, представляет собой формализованную математическую модель взаимосвязи между экономическими показателями, построенную на основе использования статистических методов.

Можно сказать, что она представляет собой частный случай экономико-математической модели, т.е. экономическую модель, представленную в математической форме.

(1.1)

Уравнение регрессии. Взаимосвязи между показателями, отражаемые в эконометрической модели, обычно описываются уравнением регрессии. Приведем упрощенный пример. Предположим, что в начальный момент времени цена на некоторую продукцию составляет 5 ден.ед., при этом каждый месяц она возрастает на 10%, т.е. в 1,1 раза. Тогда уравнение регрессии, отражающее взаимосвязь между двумя показателями: ценой продукции и временем, будет выглядеть следующим образом:

y_t = 5 * 1,1^t + ε_t,

где t – время, мес.,

y_t – цена в момент времени t,

ε_t - случайная компонента процесса на момент времени t.

Первый вопрос, который решают при построении эконометрической модели, - это вопрос спецификации.

Спецификация модели– это математическая форма записи уравнения зависимости результирующей переменной от одного или нескольких факторов. По сути, она представляет собой отбор факторов, включаемых в модель, и выбор вида уравнения регрессии.

В зависимости от спецификации эконометрических моделей классифицируют на несколько типов. Соответственно, основных классификационных признаков, связанных с классификацией, два – количество включенных факторов (т.е. экономических показателей) и тип зависимости между показателями в уравнении регрессии. Кроме того, эконометрические модели классифицируют по типу исходных данных.

По количеству включенных факторов различают два типа эконометрических моделей: модели парной и множественной регрессии.

Парная регрессия (ее еще называют – простая)представляет собой регрессию между двумя показателями, двумя переменными.

Приведенный выше пример относится к парной регрессии. В общем виде уравнение парной регрессии можно записать следующим образом:

(1.2)

y = f(x) + ε,

где y – зависимая переменная (результативный признак);

x – независимая переменная (признак-фактор);

f(x) – функция, отражающая регрессионную зависимость;

ε - случайная компонента, которая характеризует отклонение реального значения результативного признака от теоретического.

Множественная регрессия представляет собой зависимость между результативным признаком и двумя либо большим числом факторов.

В общем виде ее можно записать следующим образом:

(1.3)

y = f(x₁, x₂, …, x_n) + ε,

где y – результативный признак;

n ≥ 2 – число независимых факторов, включенных в модель;

x₁, x₂, …, x_n – признаки-факторы;

f(X) – функция, отражающая регрессионную зависимость;

ε - случайная компонента.

При использовании моделей множественной регрессии обычно, помимо построения самого уравнения регрессии и определения совокупного влияния факторов на моделируемый показатель, определяют также влияние на результат каждого фактора в отдельности.

По-другому признаки-факторы еще называют объясняющими, предикторными, экзогенными переменными, регрессорами. Зависимую, результирующую переменную y иногда называют эндогенной.

По типам зависимости, используемым в модели, можно выделить следующие типы эконометрических моделей:

1) линейная (если используется линейная зависимость между показателями) (y = ax + b[1] или y = a₁x₁ + a₂x₂ + … +a_nx_n + b);

2) нелинейная (если используется нелинейная связь). Здесь, в свою очередь, могут быть использованы различные функции:

а) полиномы различных степеней, начиная со второй, т.е.

- квадратическая функция (y = ax² + bx + c),[2]

- кубическая функция (y = ax³ + bx² + cx + d)

- и т.д.

б) степенная функция (y = ax^b)

в) гиперболическая функция (у = a/x + b)

г) показательная (экспоненциальная) функция[3] (у = aе^bx)

д) другие нелинейные функции (простая модифицированная экспонента (у = k - aе^bx); логистическая кривая (у = k / (1 - aе^bx)); функция Гомпертца у = k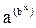и т.д.)

Более подробно каждая из этих функций будет рассмотрена при изучении темы «Нелинейные модели регрессии».

Классификация эконометрических моделей по типам данных. Кроме того, эконометрические модели можно классифицировать по типам данных. А именно, исходные данные для модели могут быть пространственными либо временными рядами.

Пространственные данные (cross-sectional data) представляют собой данные об экономических показателях на определенный момент времени (например, данные о среднем уровне дохода и среднем уровне спроса на некоторую продукцию в различных регионах позволяют исследовать зависимость между спросом и доходом).

Временные ряды (time-series data) позволяют исследовать зависимость показателя от времени (например, по данным о спросе на продукцию в одном и том же регионе в разные моменты времени позволяют провести такое исследование для спроса).

Основные проблемы, возникающие в процессе моделирования, и связанные с ними возможные ошибки. Выделим основные проблемы, возникающие в процессе моделирования, и связанные с ними возможные ошибки:

1) проблема отбора факторов, включаемых в модель

а) количество факторов

б) качественный состав факторов

Эти две стороны одной проблемы тесно взаимосвязаны. Содержательный отбор факторов очень важен, поскольку он лежит в основе спецификации модели. Чем больше факторов, влияющих на результат, будет учтено, тем более адекватной, близкой к реальности будет построенная модель. Но, с другой стороны, существует опасность включить в модель лишние факторы, которые не являются существенными в данном исследовании. Это может привести к очевидно нелепым результатам (в качестве примера можно привести анекдот о вреде огурцов: «Сколько людей, умерших в раннем возрасте, употребляло огурцы? Почти 100%, - следовательно, огурцы вредны для здоровья»).

Кроме того, чем больше факторов включено в модель, тем она сложнее, и выигрыш в адекватности может быть иногда сведен на нет трудностями, связанными с построением и использованием модели.

Иногда количество факторов, включаемых в модель, можно уменьшить за счет их агрегирования, т.е. объединения нескольких факторов в один. Кроме того, включив в модель время, можно иногда учесть не учтенные в явном виде факторы, связанные со временем.

Ошибки в спецификации модели могут быть также допущены за счет того, что признаки-факторы влияют не только на результат, но и друг на друга.

2) проблема определения связи между факторами

а) выбор функции для моделирования

б) определение параметров этой функции

Наиболее простой функцией является линейная, и в случае парной регрессии для нее необходимо определить всего два параметра. Тем не менее, не все зависимости можно моделировать с помощью этой функции. При использовании нелинейных функций также необходимо помнить о том, что выигрыш в адекватности сопровождается ростом сложности модели.

3) определение исходных данных, на основании которых будет строиться модель

а) объема выборки

б) состава выборки

При построении эконометрической модели невозможно учесть все возможные значения показателей, так как обычно их очень много и даже иногда бесконечно много. Например, исследуя зависимость спроса от дохода путем опроса потребителей, обычно невозможно опросить всех потенциальных покупателей, и опрашивают только некоторых из них. В таком исследовании все покупатели представляют собой генеральную совокупность, а опрошенные (учтенные в модели) – выборку.

Если выборка мала, то имеется мало возможных комбинаций значений показателей, и поэтому велика вероятность случайного обнаружения комбинации значений, показывающих сильную зависимость, которой на самом деле нет. Например, опросив всего пару человек из сотен, мы можем случайно столкнуться с людьми, которые при высоком доходе предъявляют небольшой спрос на данный товар, из чего сделаем неправильный вывод о зависимости между этими показателями.

Другой пример, который часто используется в теории вероятности, - подбрасывание монеты (здесь генеральная совокупность - бесконечно большое число опытов). В нормальных условиях герб или решка выпадают примерно с одинаковой частотой. Предположим, что монета повреждена, и герб выпадает в 60% случаев. Пусть объем выборки – 100 отдельных экспериментов, и герб выпал 58 раз. Это с очень большой неуверенностью позволит предположить, что монета неправильно сбалансирована, поскольку такое отклонение от ожидаемых 50% не столь велико. Для подтверждения предположения о повреждении монеты следовало бы провести большее количество экспериментов, например, 1000. Однако, если бы монета была повреждена более существенно (например, герб выпадал бы в 99% случаев), и в выборке из 100 экспериментов он выпал бы 98 раз, то тогда это послужило бы явным признаком повреждения монеты.

Минимальный объем выборки. Из последнего примера видно, что необходимый минимальный объем выборки зависит от того, насколько сильную связь исследуют.

Строя эконометрическую модель на основе выборки заданного объема, мы выдвигаем гипотезу, что существует достаточно сильная связь между показателями. В реальности эта связь может отсутствовать (назовем это нулевой гипотезой). Насколько наша гипотеза является значимой, насколько мы можем быть в ней уверены? Она тем более значима, чем меньше вероятность ее принять в случае, если на самом деле реализовалась нулевая гипотеза. Т.е вероятность того, что мы установили наличие связи, когда ее на самом деле нет, должна быть мала. Эта вероятность функционально зависит от объема выборки и от того, насколько сильную зависимость мы хотим выявить. Для определения этой вероятности используют статистические таблицы, в которых отражены значения соответствующих функций. В свою очередь, при определении объема выборки для построения эконометрической модели необходимо заранее задаться этой вероятностью.

Кроме того, необходимо помнить, что число наблюдений в выборке должно превосходить число признаков в несколько раз, чтобы параметры уравнения множественной регрессии были статистически надежными.

Большую роль также играет качественный состав выборки. Она обязательно должна быть репрезентативной, т.е. правильно отражать свойства генеральной совокупности. Для этого при определении методики отбора исходных данных необходимо исключить факторы, которые сами по себе могут повлиять на результат. Например, проводя телефонный опрос потребителей с целью выяснить их отношение к определенному виду продукции, можно получить данные в основном о тех респондентах, которые часто находятся дома, у телефона. Это может само по себе влиять на их потребительские предпочтения и, таким образом, исказить реальную ситуацию.

Коэффициент корреляции. При проведении эконометрического исследования, как правило, помимо построения уравнения регрессии, рассчитывают также показатели тесноты связи между параметрами. Один из таких показателей – коэффициент корреляции. Он измеряет тесноту линейной связи между переменными.

Коэффициент корреляции между переменными х и y рассчитывается по формуле:

(1.4)

где 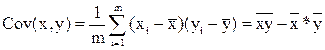- коэффициент ковариации между этими переменными;

m – число наблюдений;

x₁, x₂, … x_m; y₁, y₂, … y_m – значения переменных;

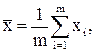
- средние значения x, y и xy;

- среднеквадратические (стандартные) отклонения значений переменных (СКО).

При этом Cov (x,x) = а Cov (y,y) = , т.е. ковариация переменной с самой собой равна ее дисперсии. Поэтому корреляция признака с самим собой всегда равна единице.

Коэффициент корреляции может принимать значения в диапазоне от
-1 (отрицательная корреляция) до 1 (положительная корреляция). Чем ближе он по модулю к единице, тем теснее линейная связь. Если его значение приближается к нулю, линейная связь между переменными отсутствует. Отметим, что коэффициент корреляции может равняться нулю тогда и только тогда, когда ковариация признаков равна нулю (это следует из формулы (1.4)): .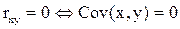

Поскольку в числителе и знаменателе формулы (1.4) находятся величины, измеряемые в одних и тех же единицах измерения (перемножаются единицы измерения показателей), коэффициент корреляции является величиной безразмерной.

Отметим, что при подстановке в (1.4) выражений для расчета ковариации и СКО m сокращается, и формула принимает вид (1.5):

(1.5)

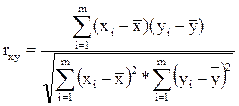
Для измерения тесноты связи используется также коэффициент детерминации, который представляет собой квадрат коэффициента корреляции и будет впоследствии рассмотрен более подробно. Отметим только, что этот коэффициент изменяется от 0 до 1, и чем он ближе к единице, тем связь теснее.

Дата добавления: 2014-01-07