Переходные процессы в линейных электрических цепях

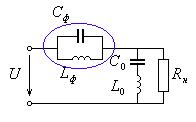
Полосовой фильтр

Резонансные фильтры

Заградительный фильтр

	Переходный процесс

Коммутация - любое изменение в электрической цепи, ведущее к переходному процессу (включение, отключение, изменение геометрии цепи, изменение параметров элементов и источников).

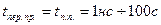
При переходном процессе на реактивных элементах может возникнуть перенапряжение или в цепи могут возникнуть скачки тока.

Возникновение

1. Скачки напряжения.

2. Есть ряд устройств, в которых переходный процесс – рабочий режим.

Идеальная коммутация:; 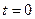- момент коммутации; - момент времени, непосредственно предшествующий коммутации; - момент времени, непосредственно следующий за коммутацией.

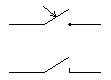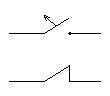ЗамыканиеРазмыкание

Причина переходных процессов – реактивные элементы.

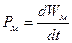; Если => 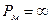, что физически недопустимо.

;

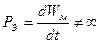
Т.е. любые изменения энергии происходят за конечное время.

Законы коммутации.

Обобщенная форма:

1-й закон:

Потокосцепление цепи непосредственно до коммутации равно потокосцеплению цепи непосредственно после коммутации. 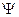не изменяется скачком.

2-й закон:

Заряд цепи непосредственно до коммутации равно заряду цепи непосредственно после коммутации. Электрическое поле цепи не меняется скачком

Для линейных цепей и корректных коммутаций:

1-й закон:

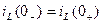Ток через L не меняется скачком

2-й закон:

U на C в момент коммутации не меняется скачком

Начальные условия:

I. Независимые начальные условия – значения токов в ветвях с индуктивностью и напряжений на емкостях. (Определяются законами коммутации).

-нулевые

а) (х.х.)

б) 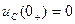(к.з.)

-ненулевые

а) => в момент коммутации дополнительный источник тока

б) 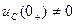=> в момент коммутации дополнительный источник напряжения

II. Зависимые начальные условия – значения тока в ветвях без индуктивности и напряжений на остальных элементах. (Определяются с использованием законов Кирхгофа и законов коммутации).

Классический метод анализа переходных процессов

Заключается в решении системы дифференциальных уравнений, описывающих состояние электрической цепи после коммутации.

II закон Кирхгофа:

- принужденный (вынужденный)

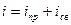
- частное решение неоднородного дифференциального уравнения, это тот ток, который установится в цепи после окончания переходного процесса.

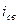- свободная составляющая перех. тока;

- общее решение однородного дифференциального уравнения;

- те токи, которые потекут в цепи с момента шундирования источника энергии.

Порядок анализа переходных процессов в электрических цепях классическим методом.

1. Записываем систему дифференциальных уравнений, описывающих электрическое состояние цепи, используя законы Кирхгофа.

2. С использованием законов коммутации определяются независимые начальные условия ()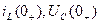

3. С использованием независимых начальных условий и законов Кирхгофа записанных для определяем зависимые начальные условия.

4. Рассчитываем принужденную составляющую, используя известные методы анализа.

5. Составляем характеристическое уравнение и находим его корни.

6. Записываем свободную составляющую в виде:

, где - k-й корень характеристического уравнения

n - степень характеристического уравнения

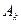- постоянная интегрирования, соответствующая

7. Определяем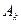

8. Решение записываем в виде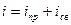

Определение степени характеристического уравнения.

Степень характеристического уравнения определяется числом основных независимых начальных условий для электрической цепи после ее упрощения.

1)

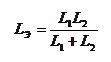
С магнитной связью:

2)

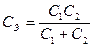
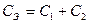
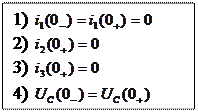
По числу начальных условий степень характеристического уравнения равна 2

Составляем характеристические уравнения:

(*)

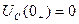
I способ: Составление по главному по главному определителю системы уравнений электрического состояния записанных для свободных составляющих.

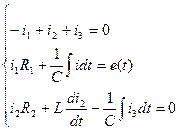с учетом (*) переписываем: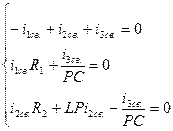

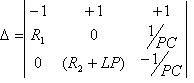
, но т.к. =>

Корни характеристического уравнения определяются из выражения

Данный метод не имеет ограничений, т.е. используется при всех видах ограничений.

II способ: По входному сопротивлению цепи (относительно любых точек).

; ;

Определение постоянных интегрирования.

n=1;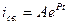

n=2;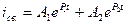

n=3;

Для определения постоянных интегрирования с помощью законов коммутации и законов Кирхгофа для момента времени определяется как значение самой искомой функции, так и всех ее производных по (n-1)-ю включительно.

n=1:

n=2:

a) корни – действительные числа < 0

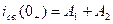
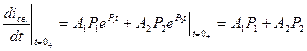
б) корни – комплексно-сопряженные

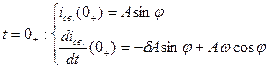
Дата добавления: 2014-01-07