
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 8 . Монотонные функции. Производная
|
|
|
|
П.1 Монотонные функции.
ОПР. Функция 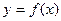 :
:  называется возрастающей на множестве E, обозначение
называется возрастающей на множестве E, обозначение 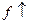 , если
, если
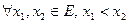
 .
.
ОПР. Функция 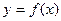 :
:  называется строго возрастающей на множестве E, обозначение
называется строго возрастающей на множестве E, обозначение 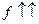 , если
, если
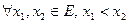
 .
.
ОПР. Функция 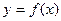 :
:  называется убывающей на множестве E, обозначение
называется убывающей на множестве E, обозначение 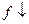 , если
, если
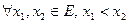
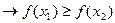 .
.
ОПР. Функция 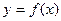 :
:  называется строго убывающей на множестве E, обозначение
называется строго убывающей на множестве E, обозначение 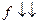 , если
, если
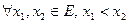
 .
.
ТЕОРЕМА 1. Если 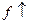 на
на 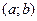 , то существует
, то существует 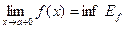 и
и 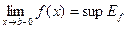 , где
, где 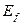 - множество значений функции
- множество значений функции 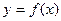 на
на 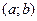 .
.
ДОК. (1) Пусть 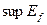 = +
= + . Тогда
. Тогда 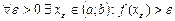 . Выберем
. Выберем 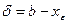 .Тогда
.Тогда 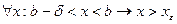 и поэтому
и поэтому 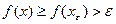 , т.е.
, т.е. 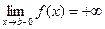 .
.
(2) Пусть 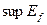 =В
=В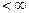 . Тогда
. Тогда 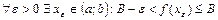 .
.
Выберем 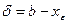 . Тогда
. Тогда 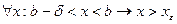 и поэтому
и поэтому  , т.е.
, т.е.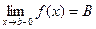 .
.
(3) Пусть 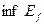 = - ¥. Тогда
= - ¥. Тогда 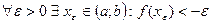 .
.
Выберем 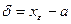 .Тогда
.Тогда 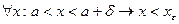 и поэтому
и поэтому  , т.е.
, т.е. 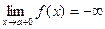 .
.
(4) Пусть 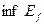 = А. Тогда
= А. Тогда 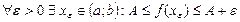 .
.
Выберем 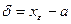 , тогда
, тогда 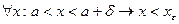 и поэтому
и поэтому 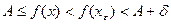 ,т.е.
,т.е. 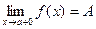 .
.
СЛЕДСТВИЕ 1. Если 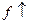 на
на 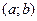 , то для любого
, то для любого 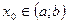 существуют
существуют 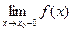 и
и 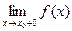 .
.
ТЕОРЕМА 2. Если 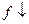 на
на 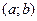 , то существует
, то существует 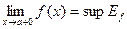 и
и  , где
, где 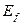 - множество значений функции
- множество значений функции 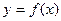 на
на 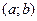 .
.
ДОК. Достаточно применить теорему 1 для функции 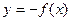 .
.
СЛЕДСТВИЕ 2. Если 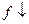 на
на 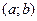 , то для любого
, то для любого 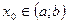 существуют
существуют 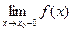 и
и 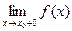 .
.
ТЕОРЕМА 3.(о существовании обратной функции)
Если 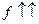 (или
(или 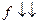 ) непрерывная функция на [a;b], то существует и единственная обратная к ней функция
) непрерывная функция на [a;b], то существует и единственная обратная к ней функция  , определенная на отрезке
, определенная на отрезке 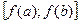 и непрерывная, строго возрастающая (или убывающая) на этом отрезке.
и непрерывная, строго возрастающая (или убывающая) на этом отрезке.
ДОК. Пусть 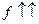 и непрерывна на [a;b]. Тогда
и непрерывна на [a;b]. Тогда 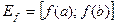 и для любого
и для любого 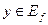 существует и единственное значение
существует и единственное значение 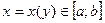 , для которого
, для которого 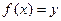 . Действительно, если таких значений два
. Действительно, если таких значений два 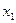 и
и 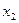 , например
, например 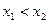 , то
, то 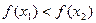 . Положим
. Положим 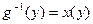 . Тогда
. Тогда 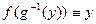 на
на 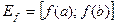 , т.е.
, т.е.  обратная к
обратная к  функция. Докажем ее непрерывность на
функция. Докажем ее непрерывность на 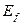 . Пусть
. Пусть 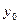 произвольная точка интервала
произвольная точка интервала  и
и 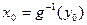
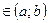 . Тогда для любого
. Тогда для любого
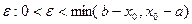 существует
существует 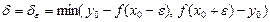 такое, что
такое, что 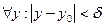 выполняется неравенство
выполняется неравенство 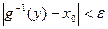 . Строгое возрастание функции
. Строгое возрастание функции  следует из неравенств:
следует из неравенств:  .
.
Непрерывность функции  в граничных точках
в граничных точках 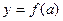 и
и 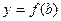 следует из теоремы 1:
следует из теоремы 1: 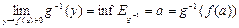 ,
,
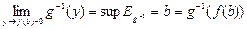
П.2. Производная функции в точке.
ОПР. 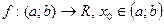 . Производной функции
. Производной функции 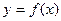 в точке
в точке 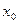 , называют число
, называют число 
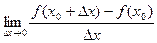 .
.
ПРИМЕР 1 Вычислить производную функции 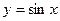 в произвольной точке x.
в произвольной точке x.
РЕШЕНИЕ. 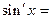
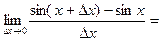
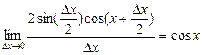 .
.
МЕХАНИЧЕСКИЙ смысл производной.
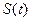 - путь, пройденный материальной точкой к моменту времени t,
- путь, пройденный материальной точкой к моменту времени t,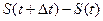 - расстояние, пройденное точкой за время
- расстояние, пройденное точкой за время 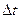 ,
, - средняя скорость движения,
- средняя скорость движения,
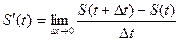 - скорость в момент времени t.
- скорость в момент времени t.
ГЕОМЕТРИЧЕСКИЙ смысл производной.
Точки 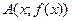 и
и 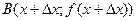 на графике функции
на графике функции 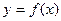 соединены прямой Lсек – секущей,
соединены прямой Lсек – секущей,  -
-
угловой коэффициент прямой Lсек  .
.
При 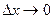 прямая Lсек поворачивается вокруг точки А, занимая предельное положение - - касательной к графику функции в точке А.
прямая Lсек поворачивается вокруг точки А, занимая предельное положение - - касательной к графику функции в точке А.
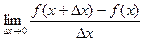 - угловой коэффициент (тангенс угла наклона) касательной. Производная функции
- угловой коэффициент (тангенс угла наклона) касательной. Производная функции 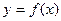 в точке x равна тангенсу угла наклона касательной, проведенной к графику функции в точке с абсциссой x.
в точке x равна тангенсу угла наклона касательной, проведенной к графику функции в точке с абсциссой x.
ТЕОРЕМА 4 (о непрерывности дифференцируемой функции)
Если функция 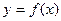 имеет производную в точке
имеет производную в точке 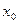 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
ДОК. 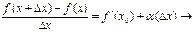
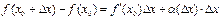 .
.
Тогда 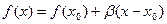 , где
, где 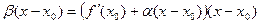 - бесконечно малая функция в точке
- бесконечно малая функция в точке 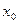 ., т.е.
., т.е.  .
.
ПРИМЕР 2. Функция 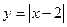 непрерывна в точке
непрерывна в точке 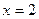 , но не имеет производной в этой точке.
, но не имеет производной в этой точке.
РЕШЕНИЕ. 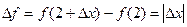 - бесконечно малая функция в точке
- бесконечно малая функция в точке 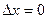 , т.е.функция
, т.е.функция 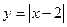 непрерывна в точке
непрерывна в точке 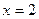 .Функция
.Функция 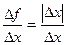 не имеет предела в точке
не имеет предела в точке 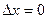 , поскольку
, поскольку 
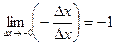 ,
,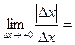
 и пределы справа и слева не совпадают.
и пределы справа и слева не совпадают.
ТЕОРЕМА 5. (арифметическая теорема о производных)
Если функции 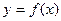 и
и 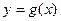 имеют производную в точке
имеют производную в точке 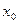 , то
, то
(1) 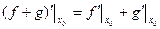
(2)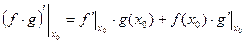
(3)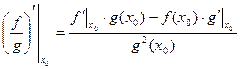 , при
, при 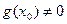 .
.
ДОК. (2) 
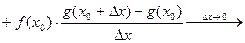
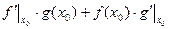 ,
,
т.к. функция 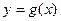 непрерывна в точке
непрерывна в точке 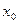 (теорема 4).
(теорема 4).
(3) 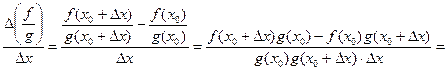
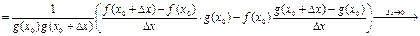
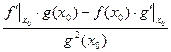 , поскольку при
, поскольку при 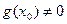 функция
функция
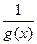 непрерывна в точке
непрерывна в точке 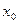 (теорема 4).
(теорема 4).
(1) доказать самостоятельно.
УПРАЖНЕНИЯ.
1) Докажите непосредственно, что 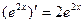 .
.
2) Найдите функцию обратную к функции 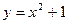 на
на  .
.
3) Функция 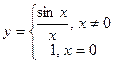 . Найдите производную функции в точке
. Найдите производную функции в точке 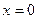 .
.
ВОПРОСЫ К ЭКЗАМЕНУ.
1) Монотонные функции. Теорема о существовании предела монотонной функции.
2) Теорема о существовании и непрерывности обратной
функции.
3) Понятие производной функции, ее механический и геометрический смысл. Примеры.
4) Теорема о непрерывности функции, имеющей производную.
5) Арифметическая теорема о производных.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 513; Нарушение авторских прав?; Мы поможем в написании вашей работы!