Надёжность системы с восстановлением

До сих пор, рассматривая задачи надежности, мы исходили из того, что отказавший элемент выходит из строя окончательно и, никакого восстановления его функций не производится. Представляет интерес исследование задач надежности, где отказавшие элементы восстанавливаются, т.е. мгновенно заменяются новыми или ремонтируются.

При решении такого рода задач мы будем предполагать, что все потоки событии, переводящие систему из состояния в состояние – простейшие (иначе мы с такими задачами не справимся).

Предварительно сделаем следующее замечание: все процессы, связанные с надежностью систем, которые мы рассматривали до сих пор, были существенно нестационарными; так как восстановления элементов не было, естественно, что при t® ¥ надежность системы стремилась к нулю, и "предельным режимом" системы просто было «не работает».

В задачах с восстановлением нас будут интересовать не только переходные процессы в системе, но и установившиеся режимы при t®¥. В данном параграфе мы рассмотрим несколько задач из области надежности систем с восстановлением.

Задача 1. (задача о запасных элементах).

Работает простая система, состоящая из одного элемента Э, который подвергается простейшему потоку отказов с интенсивностью l. При отказе элемент мгновенно заменяется новым с таким же характеристиками. В нашем распоряжении имеется N запасных элементов, находящихся в «холодном» резерве. Определить вероятность того, что этого числа запасных элементов нам хватит для обеспечения работы системы в течение времени t (другими словами, найти надежность P(t) системы с восстановлением).

Решение. Нетрудно заметить, что поставленная задача эквивалентна задаче оценки надежности резервированной системы с N резервными элементами, работающими в холодном резерве и, как таковая, может быть решена методами, предложенными выше. Но мы решим ее несколько иным, более простым методом.

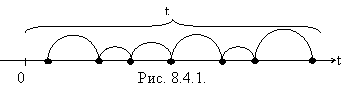
Рассмотрим на оси 0 t «поток восстановления», т.е. последовательность моментов времени, в которые выходят из строя и мгновенно восстанавливаются элементы (рис.8.4.1). Очевидно это – простейший поток с интенсивностью l. Надежность системы P (t) есть вероятность того, что к моменту t система будет работать. Для этого нужно, чтобы на участке (0, t) отказало не более N элементов (один основной и N – 1 запасных).

Мы знаем, что число событий простейшего потока, попадающих на участок длиной t, распределено по закону Пуассона: ,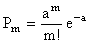

где a=lt, т.е.

(m=0,1,…). (8.4.1)

Найдем вероятность того, что число точек (событий), попадающих на участок (0,t), будет не больше N. Эта вероятность и будет надежностью системы

P(t)=P₀+P₁+…+P_N,

или, короче, 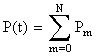. (8.4.2)

Подставляя (8.4.1) в (8.4.2), получим:

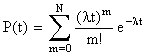, (8.4.3)

или, вынося e^-lt за знак суммы, 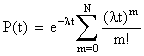. (8.4.4)

Вычисления по формулам (8.4.3) или (8.4.4) удобно производить, пользуясь таблицами пуассоновского распределения P_m (или вероятностей 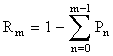, которые несколько удобнее табулируются).

Пример 1. Рассматривается работа элемента с восстановлением (задача 1); интенсивность потока отказов l=2 (отказа в час). В нашем распоряжении N=6 запасных элементов. Определить надежность системы P(t) в функции времени до t=5 час (максимальное время работы).

Решение. Воспользуемся таблицей значений распределения Пуассона. Первый столбец таблицы, где P ₇ отлично от нуля – это столбец, соответствующий a =1, т.е. t =0.5. Полагая t = 0.5 и складывая все вероятности для m > 6 (из них отлична от нуля только P₇), получаем: P (0,5) = 1 – 0,0001 = 0,9999.

Для t =1 (a =2) имеем: P (1) = 1 – (0,0037 + 0,0009 + 0,0002) =1 – 0,0048 = 0,9952 ≈ 0,995.

Для t=2 (a=4):

P (2) =1- (0,0595 + 0,0298 + 0,0132 + 0,0053 + 0,0019 + 0,0006 + + 0,0002 + 0,0001) = 1 – 0,1106 ≈0,889.

Для t=3 (a=6) уже удобнее не переходить к противоположному событию, а вычислять вероятность того, что число отказов будет меньше семи:

P (3) = 0,0025 + 0,0149 + 0,0466 + 0,0892 + 0,1339 + 0,1606 + 0,1606 ≈ 0,608.

Для t=4 (a=8): P (4) = 0,0003 + 0,0027 + 0,0107 + 0,0286 + 0,0572 +0,0916 + 0,1221 ≈ 0,313.

Для t=5 (a=10):

P (5) = 0,0000 + 0,0005 + 0,0023 + 0,0076 + 0,0189 + 0,0378 + 0,0631 ≈ 0,130.

Наносим полученные значения на график (рис. 8.4.2)

Задача 2. Система состоит не из одного, как в задаче 1, а из нескольких элементов; среди них

n₁ элементов группы 1,

n₂ элементов группы 2,

……………………

n_k элементов группы k.

Каждый из элементов любой группы, независимо от других, может отказывать; интенсивность потока отказов для элементов разных групп равна соответственно: l₁, l ₂, …, l _k.

Все потоки отказов – простейшие. Отказавший элемент немедленно заменяется новым. В запасе имеется N₁, N₂,..., N_k элементов соответствующих групп. Отсутствие запасного элемента при очередном отказе означает отказ устройства. Требуется определить надежность системы P(t).

Решение. Так как отсутствие запасного элемента любой группы равносильно отказу устройства, будем рассматривать группы как «последовательно» включенные элементы; тогда надежность системы будет равна произведению надежностей всех групп. Надежность i-ой группы определяется как в задаче 1:

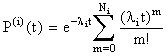(8.4.5)

Перемножая эти надежности, получим надежность системы: P(t)=P⁽¹⁾(t)× P⁽²⁾(t)×… × P^(k)(t),

или, короче, 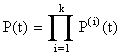. (8.4.6)

Заметим, что, пользуясь выведенными формулами, можно не только оценивать надежность системы при заданном числе запасных элементов, но и определять, сколько запасных элементов нужно иметь в распоряжении для того, чтобы система при заданном t имела определенную надежность.

Пример 2. Определить число запасных элементов N, которое надо иметь в распоряжении для того, чтобы система, состоящая из одного основного элемента и N запасных с интенсивностью потока отказов l=0.5, имела при t =8 надежность не меньше 0,95.

Решение. Имеем a =lt=4. В столбце таблицы значений распределения Пуассона, соответствующем a =4, складываем все вероятности, начиная с последней, до тех пор, пока сумма не дойдет до

1 – 0,95 = 0,05.

Получаем: 0,0001+ 0,0002 + 0,0006 + 0,0019 + 0,0053 + 0,0132 + 0,0298 = 0,0511.

Итак, вероятность того, что число отказавших элементов будет больше семи, равна 0,0511, т.е. N=7 не удовлетворяет нашему требованию; если же взять N = 8, то вероятность нехватки элементов будет меньше 0,05: 0,0001+ 0,0002 + 0,0006 + 0,0019 + 0,0053 + 0,0132 = 0,0213.

Отсюда, число запасных элементов, удовлетворяющее условию задачи, N = 8.►

Во всех рассмотренных выше задачах восстановление элемента происходило мгновенно, теперь мы рассмотрим задачу, где оно задерживается.

Задача 3 (система из одного элемента с задержанным восстановлением).

Система состоит из одного элемента Э₁, находящегося под действием простейшего потока отказа с интенсивностью l. Отказавший элемент немедленно начинает восстанавливаться (ремонтироваться). Поток восстановления ¾ простейший, с интенсивностью m. Запас средств для ремонта неограничен. Требуется определить:

¾ обобщенную надежность системы P(t) – вероятность того, что в момент t система будет работать;

¾ предельное значение обобщенной надежности p - вероятность того, что в произвольный, достаточно удаленный от начала момент система будет работать;

¾ вероятность 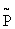(t) того, что до определенного момента система будет работает вообще безотказно (т. е. не будет ни одного перерыва в работе для восстановления).

Решение. Состояния системы (в данном случае элемента) будут:

S₀ - работает,

S₁ - восстанавливается.

Граф состояний показан на рис. 8.4.3.

Из состояния S₀ в S₁ систему переводит поток отказов с интенсивностью l; из S₀ в S₁ - поток восстановлений с интенсивностью m.

Обозначим вероятности состояний p₀(t) и p₁(t). Составим дифференциальные уравнения Колмогорова для вероятностей состояний. Имеем:

Из данных уравнений одно является лишним, так как р₀ и р₁ связаны соотношением p₀(t)+p₁(t)=1. Учитывая это, отбросим второе уравнение, а в первое подставим вместо p₁ его выражение (1-р₀)

,

или .

Это уравнение естественно решать при начальных условиях: р₀(0)=1, р₁(0)=0

(в начальный момент система работает).

Данное линейное дифференциальное уравнение с одной неизвестной функцией р₀ легко может быть решено не только для простейшего потока заявок (l=const), но и для случая, когда интенсивность этого потока со временем меняется (l=l(t)). Не останавливаясь на последнем случае, приведем решение этого уравнения только для случая l=const:

.

Тогда для системы вероятности состояний будут иметь следующий вид:

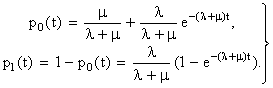(8.4.7)

Обобщенная надежность системы ¾ вероятность того, что в момент t она будет работать:

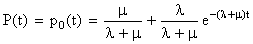. (8.4.8)

При t ® ¥ эта надежность стремится к предельному значению: ,

т. е. равна относительной доле интенсивности потока восстановления в суммарной интенсивности потока восстановления и отказов.

Вероятность 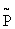(t) того, что до момента t не произойдет ни одного отказа, определим следующим образом. Предположим, что восстановлений отказавшего элемента нет, т. е. граф состояний имеет вид, показанный на рис. 8.4.4.

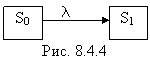
Искомая вероятность 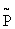(t) будет равна вероятности 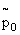(t) того, что система с графом состояний, показанным на рис.8.4.4, будет к моменту t в состоянии S₀; эта вероятность получится решением дифференциального уравнения ,

откуда .

Таким образом, 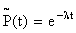. (8.4.9)

Задача 4 (система из нескольких элементов с задержанным восстановлением).

Система S состоит из n элементов, каждый из которых находится под действием простейшего потока отказов с интенсивностью l. При отказе любого элемента система выключается и начинается восстановление элемента. При неработающей системе элементы отказывать не могут. Интенсивность потока восстановления равна m. Все потоки - простейшие. Найти:

- обобщенную надежность системы P(t) (вероятность того, что в момент t система будет работать);

- предельную обобщенную надежность системы p;

- вероятность 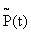того, что до момента t отказов вообще не будет.

Решение. Система по-прежнему может быть только в двух состояниях:

S₀- работает,

S₁ - выключена, восстанавливается один элемент (одновременный выход из строя двух или более элементов не рассматривается в силу ординарности потока отказов).

Граф состояний показан на рис. 8.4.5.

Как видно, он отличается от графа на рис. 8.4.3 только тем, что вместо l стоит nl. Отсюда на основе решения предыдущей задачи,

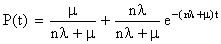(8.4.10)

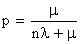(8.4.11)

. (8.4.12)

Иную картину мы получим, если предположим, что во время восстановления одного элемента другие продолжают работать и могут выходить из строя.

Задача 5. Система S состоит из n элементов, каждый из которых находится под действием потока отказов (неисправностей) с интенсивностью l. При отказе элемента он немедленно начинает восстанавливаться, остальные же элементы продолжают работать (активно или в горячем резерве). Интенсивность потока восстановлений элемента (независимо от числа одновременно восстанавливаемых элементов) равна m.

Найти:

- вероятность Р(t) того, что в момент t все элементы будут исправны;

- предельную вероятность того же события;

- среднее число исправно работающих элементов для предельного режима (при t®¥).

Решение. Будем нумеровать состояния системы по числу неисправных элементов:

S₀ - все элементы исправны;

S₁ - один элемент восстанавливается, остальные исправны;

.................................

S_k - k элементов восстанавливаются, остальные исправны;

.................................

S_n - все n элементов восстанавливаются.

Граф состояний системы показан на рис. 8.4.6.

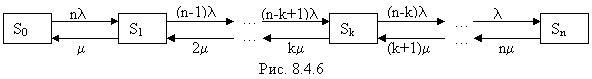
Дифференциальные уравнения имеют вид:

(8.4.13)

плюс условие p₀+p₁ + p₂ + … + p_n =1.

Искомая вероятность P(t) есть не что иное, как p₀(t), которую получим, интегрируя систему уравнений (8.4.13) при начальных условиях: t = 0; p_o = 1; p₁ = … = p_n = 0.

Предельные вероятности состояний, полагая l/m=r, будут иметь следующий вид:

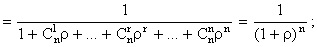
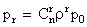; r=1, …, n.

Искомая предельная вероятность p будет равна предельной вероятности p₀.

Среднее число исправно работающих элементов будет равно числу элементов n, умноженному на вероятность того, что отдельный элемент работает исправно. Эта вероятность для предельного режима равна 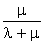, откуда

.

Рассмотренные задачи и примеры показывают, что математический аппарат, применяемый для анализа надежности технических устройств, в сущности, совпадает с аппаратом теории массового обслуживания, и исследование процессов, протекающих в системах с ненадежными элементами, при известных условиях может быть проведено методами теории непрерывных марковских цепей. Для этого нужно, чтобы потоки событий, переводящие элементы из состояния в состояние, были (точно или приближенно) пуассоновскими. Эти потоки необязательно должны быть стационарными, но во всяком случае такими, чтобы интенсивности потоков событий не зависели от случайных моментов переходов системы из состояния в состояние. Для наиболее простого, стационарного случая это означает, что, в частности, все законы надежности должны быть экспоненциальными, а законы распределения времени восстановления – тоже показательными или близким к показательным.

Дата добавления: 2014-01-07