Понятие неопределенного интеграла

Определение. Если функция F (x) является первообразной для функции f (x). То выражение F (x) + с называется неопределенным интегралом от функции f (x) и обозначается символом

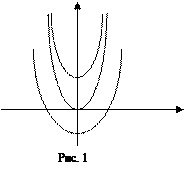
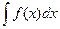
то есть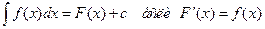

При этом функция f (x) называется подынтегральной функцией f (x)dx – подынтегральным выражением; 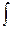- знак интеграла.

Вывод. Неопределенный интеграл представляет собой семейство функций F (x) + С.

Определение. Нахождение первообразной для данной функции f (x) называется интегрированием этой функции.

Определение. С геометрической точки зрения неопределенный интеграл представляет семейство кривых, зависящих от одного параметра, каждая из которых получается путем сдвига одной из них параллельно самой себе вдоль оси оу (рис 1). (Геометрический смысл неопределенного интеграла).

Пример f (x) = 2х

F (x) = х² + С

Давая С различные значения, получаем семейство кривых.

Дата добавления: 2014-01-07