Несобственные интегралы

Формула интегрирования по частям.

Формула инте­грирования по частям для определённого интеграла прини­мает вид:

.

Пример 3. Вычислить

Решение. Положим

.

Тогда

.

Поэтому

Несобственным интегралом от функции 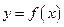, определенной на промежутке и интегрируемой по любому отрезку называется предел интеграла при .

.

Если существует конечный предел , то несобственный интеграл называется сходящимся, если же предел не существует или он бесконечный, то интеграл называется расходящимся.

Аналогично определяется интеграл , а именно

.

Несобственный интеграл с двумя бесконечными пределами определяется следующим образом:

,

где - любое действительное число.

Пример 1. Найти несобственные интегралы или установить их расходимость:

1) ; 2) ; 3) .

Дата добавления: 2014-01-07