Порядок алгоритма

Критерием оценки эффективности алгоритма является его порядок. Порядком алгоритма называется функция O(n), позволяющая оценить зависимость времени выполнения алгоритма от объема обрабатываемых данных (n – количество элементов). Говорят, алгоритм принадлежит классу O(f(n)), где f(n) – некоторая функция от n. Такое обозначение читается как «О большое от f(n)» или менее строго «пропорционально f(n)». Например, алгоритм последовательного поиска принадлежит к классу O(n), а бинарный – к классу O(log(n)). Эффективность тем выше, чем меньше время его выполнения зависит от объема данных.

Поскольку для положительных чисел log(n) < n, можно сделать вывод, что бинарный поиск всегда быстрее последовательного. Предположим, экспериментально определено, что некоторый алгоритм принадлежит к классу O(n²+n). Следовательно, можно подобрать константу k, для которой:

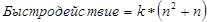
Отсюда видно, что умножение математической функции внутри скобок в О-нотации на константу не оказывает влияния на смысл нотации. Например, O(3*f(n)) эквивалентно O(f(n)), поскольку 3 можно вынести как коэффициент пропорциональности. Кроме того, если величина n достаточно велика при тестировании алгоритма, можно утверждать, что влияние члена «n» поглощается «n²». Поэтому алгоритм O(n²+n) эквивалентен O(n²). То же справедливо и для высших степеней, например, влияние «n²» будет поглощено «n³». В свою очередь, влияние log(n) будет поглощаться членом n.

Предположим, некоторый алгоритм выполняет несколько различных задач. Первая задача принадлежит к классу O(n), вторая – к классу O(n²), третья – к классу O(log(n)). Требуется определить быстродействие алгоритма в целом. Ответом будет O(n²), поскольку к этому классу принадлежит доминантная часть алгоритма.

Таким образом, значения О большого являются репрезентативными только для больших значений n. Для маленьких значений О-нотация не имеет смысла, а на общий результат оказывают влияние другие члены нотации.

Предположим, проводится тестирование двух алгоритмов. Эмпирическим путем выведены следующие зависимости:

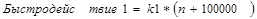
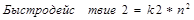
Константы k1 и k2 сравнимы по величине. Если следовать О-нотации, предпочтительнее будет первый алгоритм, поскольку он принадлежит к классу O(n). Однако, если известно, что в реальных условиях n не будет превышать 100, более эффективным окажется второй алгоритм. Следовательно, алгоритм нужно выбирать не только основываясь на O-нотации, но и исходя из условий его применения и статистических данных о времени его выполнения.

O-нотация относится к среднему случаю. Определенные условия выполнения алгоритма и исходных данных позволяют получить лучший и худший случай. Например, при последовательном поиске в массиве данных элемента, расположенного в самом начале, приведет к его обнаружению на первой же итерации цикла. Такая ситуация известна как лучший случай и ее можно представить как O(1) (выполнение алгоритма занимает одно и то же время независимо от количества элементов).

Если бы искомый элемент располагался бы всегда в конце массива, последовательный поиск был бы очень медленным и его порядок равен O(n). Такая ситуация известна как худший случай. Для бинарного алгоритма поиска лучший случай соответствует расположению искомого элемента точно посередине массива. Тем не менее, быстродействие бинарного поиска в худшем случае намного выше, чем для последовательного.

В общем случае при выборе алгоритма следует учитывать значения в О-нотации для среднего и худшего случаев. Лучшие случаи, как правило, не интересны, поскольку обычно обеспокоены граничными условиями, по которым судят о быстродействии.

Большинство алгоритмов с точки зрения порядка сводятся к трем основным типам: степенным O(n^a), линейным O(n) и логарифмическим O(log_an). Эффективность степенных алгоритмов считается плохой, линейных – удовлетворительной, логарифмических – хорошей. Аналитическое определение порядка алгоритма сложно, но в большинстве случаев возможно. В реальных задачах имеются ограничения, определяемые как логикой задачи, так и свойствами конкретной вычислительной среды, которые могут помогать или мешать и существенно влиять на эффективность конкретной реализации алгоритма. Поэтому выбор того или иного алгоритма всегда остается за разработчиком.

Дата добавления: 2014-01-07