Массивы

Массив – структура данных, характеризуемая:

- фиксированным набором однотипных элементов;

- каждый элемент имеет уникальный набор значений индексов.

Количество индексов определяют мерность массива, например, два индекса – двумерный массив, три индекса – трехмерный массив, один индекс – одномерный массив или вектор. Обращение к элементу массива выполняется по имени массива и значениям индексов для данного элемента.

Другое определение: массив – вектор, каждый элемент которого – вектор. Синтаксис описания массива представляется в виде:

< Имя >: array [n1..k1] [n2..k2]..[nn..kn] of < Тип >.

Для двумерного массива:

m: array [n1..k1] [n2..k2] of < Тип > или

m: array [n1..k1, n2..k2] of < Тип >

Двумерный массив можно представить в виде таблицы из (k1-n1+1) строк и (k2-n2+1) столбцов. Для двумерного массива, состоящего из (k1-n1+1) строк и (k2-n2+1) столбцов физическая структура представлена в табл. 4.4.

Табл. 4.4. Представление массива m.

Смещение	+0	+SizeOf(тип)	…	+(k2-n2)*SizeOf(тип)
Идентификатор	m[n1,n2]	m[n1,n2+1]	…	m[n1,k2]
…
m[k1,n2]	m[k1,n2+1]	…	m[n1,k2]
+(k1-n1)*(k2-n2+1)* SizeOf(тип)	+((k1-n1)*(k2-n2)+1)* SizeOf(тип)	…	+((k1-n1)*(k2-n2+1)+ (k2-n2))*SizeOf(тип)

Многомерные массивы хранятся в непрерывной области памяти. Размер слота определяется базовым типом элемента массива. Количество элементов массива и размер слота определяют размер памяти для хранения массива. Принцип распределения элементов массива в памяти определен языком программирования. Так в языке FORTRAN элементы распределяются по столбцам (быстрее меняется левые индексы), в PASCAL – по строкам (изменение индексов выполняется в направлении справа налево).

Количество байтов памяти, занятых двумерным массивом, определяется по формуле:

ByteSize = (k1-n1+1)·(k2-n2+1)·SizeOf(Тип) (4.3)

Адресом массива является адрес первого байта начального элемента массива.

Смещение элемента массива m[i1,i2] равно:

ByteNumber = [(i1-n1)·(k2-n2+1)+(i2-n2)]·SizeOf(Тип) (4.4)

а его адрес:

@ByteNumber = @m + ByteNumber

Например:

var m: array [3..5][7..8] of Word;

Базовый тип элемента Word требует два байта памяти, тогда таблица смещений элементов массива относительно @m будет следующей как показано в табл. 4.5. Массив будет занимать в памяти: (5-3+1) · (8-7+1) · 2 = 12 байт

адрес элемента m[4,8] равен:

@m+((4-3) · (8-7+1)+(8-7)) · 2 = @m+6

Табл. 4.5. Представление массива m.

Смещение	Идентификатор
+0	m[3,7]
+2	m[3,8]
+4	m[4,7]
+6	m[4,8]
+8	m[5,7]
+10	m[5,8]

Таким образом, преимущество использования массивов заключается в быстром вычислении адресов элементов. Независимо от значения элемента, алгоритм вычисления будет одним и тем же. Другими словами, получение доступа к элементу с индексом n принадлежит к классу операций O(1) и не зависит от величины n.

Недостаток массивов связан с ресурсоемкими операциями вставки и удаления элементов. При вставке элемента с индексом i в общем случае следует все элементы с индексами с i по n переместить на одну позицию, чтобы освободить место под новый элемент. Фактически, следует выполнить следующий код:

{ сначала освободить место под новый элемент }

for j:=n downto i do

m[j+1]:=m[j];

{ вставить новый элемент в позицию с индексом i }

m[j]:=a;

{ увеличить значение длины массива на единицу }

Inc(n);

Чем больше количество элементов, тем больше времени потребуется на выполнение операции. Следовательно, операция вставки элемента в массив принадлежит к классу O(i). Та же ситуация и для удаления элемента из массива. Но в этом случае удаление элемента с индексом i означает перемещение всех элементов, начиная с индекса i+1 и до конца массива, на одну позицию к началу массива, чтобы «закрыть» образовавшуюся «дыру». Удаление так же принадлежит к классу O(i).

{ удалить элемент, переместив следующие

за ним элементы на одну позицию вперед }

for j:=i+1 to n do

m[j-1]:=m[j];

{ уменьшить значение длины массива на единицу }

Dec(n);

Открытые массивы. В языке Паскаль доступны для работы массивы открытого типа. Приведем пример объявления открытого массива, элементами которого являются вещественные числа:

var m: array of Real;

В отличие от приведенных выше способов такое объявление не резервирует память под массив, т.к. размеры его заранее не известны. Память будет выделена в процессе выполнения с помощью процедуры SetLength. В следующем примере выделяется память для хранения ста вещественных чисел, индексируемых от 0 до 99:

SetLength(m, 100);

Для массивов открытого типа не следует использовать процедуры управления динамической памятью и символ разыменования «^». Для освобождения памяти, отводимой под открытый массив, переменной следует присвоить значение nil или передать ее в качестве аргумента процедуре Finalize:

Finalize(m);

Процедура линеаризации. Основная операция физического уровня над массивом – доступ к заданному элементу. Как только реализован доступ к элементу, над ним может быть выполнена любая операция, имеющая смысл для типа данных, которому соответствует элемент. Преобразование логической структуры массива в физическую называется процессом линеаризации, в ходе которого многомерная логическая структура преобразуется в одномерную физическую.

В соответствии с формулами (4.3), (4.4) и по аналогии с вектором (4.1), (4.2) для двумерного массива с границами изменения индексов , размещенного в памяти по строкам, адрес элемента с индексами может быть вычислен как:

(3.5)

Обобщая (3.5) для массива произвольной размерности :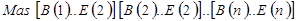

(4.6)

где 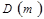зависит от способа размещения массива.

При размещении по строкам:

,

где и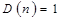

при размещении по столбцам:

,

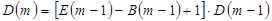где 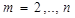и .

При вычислении адреса элемента наиболее сложным является вычисление третьей составляющей формулы (4.6), т.к. первые две не зависят от индексов и могут быть вычислены заранее. Для ускорения вычислений множители 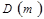могут быть вычислены заранее и сохраняться в дескрипторе массива.

Дескриптор массива содержит:

- начальный адрес массива ;

- число измерений в массиве n;

- постоянную составляющую формулы линеаризации (первые две составляющие 4.6);

- для каждого из n измерений массива: значения граничных индексов и множитель формулы линеаризации .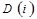

Специальные массивы. На практике встречаются массивы, которые в силу определенных причин должны записываться в память не полностью, а частично. Это особенно актуально для массивов настолько больших размеров, что для их хранения в полном объеме памяти может быть недостаточно. К таким массивам относятся симметричные и разреженные массивы.

Двумерный массив, в котором количество строк равно количеству столбцов называется квадратной матрицей. Симметричный массив – квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, попарно равны друг другу.

Для симметричной матрицы порядка n в физической структуре достаточно отобразить не n², а лишь n·(n+1)/2 элементов. В памяти необходимо представить только верхний (включая диагональ) треугольник квадратной логической структуры. Доступ к треугольному массиву организуется таким образом, чтобы можно было обращаться к любому элементу исходной логической структуры, в том числе и к элементам, значения которых хотя и не представлены в памяти, но могут быть определены на основе значений симметричных им элементов.

Для работы с симметричной матрицей должны быть определены процедуры:

- преобразования индексов матрицы в индекс вектора;

- формирования вектора и записи в него элементов верхнего треугольника элементов исходной матрицы;

- получения значения элемента матрицы из ее упакованного представления. Обращение к элементам исходной матрицы выполняется опосредованно, через указанные функции.

Разреженный массив – массив, большинство элементов которого равны между собой, так что хранить в памяти достаточно лишь небольшое число значений отличных от основного (фонового) значения остальных элементов. Различают два типа разреженных массивов:

- массивы, в которых местоположения элементов со значениями, отличными от фоновых, могут быть математически описаны;

- массивы со случайным расположением элементов.

В случае работы с разреженными массивами вопросы размещения их в памяти реализуются на логическом уровне с учетом их типа. К первому типу массивов относятся массивы, у которых местоположения элементов со значениями отличными от фонового, могут быть математически описаны, т.е. в их расположении есть какая-либо закономерность. Элементы, значения которых являются фоновыми, называют нулевыми; элементы, значения которых отличны от фонового, – ненулевыми. Нужно помнить, что фоновое значение не всегда равно нулю.

Ненулевые значения хранятся, как правило, в одномерном массиве, а связь между местоположением в исходном, разреженном, массиве и в новом, одномерном, описывается математически с помощью формулы, преобразующей индексы массива в индексы вектора.

Для работы с разреженным массивом должны быть определены функции:

- преобразования индексов массива в индекс вектора;

- получения значения элемента массива из ее упакованного представления по двум индексам (строка, столбец);

- записи значения элемента массива в ее упакованное представление по двум индексам.

Ко второму типу массивов относятся массивы, у которых местоположения элементов со значениями, отличными от фоновых, не могут быть математически описаны, т.е. в их расположении нет закономерности.

Дата добавления: 2014-01-07