Уравнение Бернулли для струйки и потока реальной жидкости

Если по элементарной струйке движется реальная жидкость, то возникают силы трения и часть полной механической энергии переходит в тепловую энергию, которая в уравнении (3.24) не учитывается. Поэтому полная механическая энергия в начале струйки будет больше, чем в конце. Потерей напора или потерей полной удельной энергии h_1-2 - называется разность полных удельных энергий в начале и в конце элементарной струйки.

.

(3.29)

Тогда уравнение для элементарной струйки реальной жидкости запишется:

.

(3.30)

Рассмотрим поток жидкости. Поток жидкости состоит из элементарных струек, скользящих друг относительно друга с разными скоростями. Пусть за время dt = 1 через поперечное сечение элементарной струйки проходит масса dm = r u dw. Осредним уравнение Бернулли для элементарной струйки реальной жидкости по поперечному сечению. Так, как в поперечном сечении давление распределяется по гидростатическому закону, сумма первых двух слагаемых постоянна и при осреднении не изменится. Усредняя третье слагаемое и выражая его через среднюю скорость, получим

.

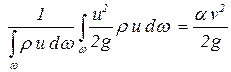(3.31)

Тогда для потока реальной жидкости уравнение Бернулли запишется:

.

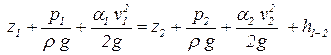(3.32)

где z – расстояние от плоскости сравнения до любой точки поперечного сечения, м;

p – давление именно в этой точке, Па;

v – средняя скорость в данном поперечном сечении, м/с;

a – имеет три названия: коэффициент неравномерности распределения скоростей, средняя коэффициент Кариолиса, коэффициент кинетической энергии.

Коэффициент неравномерности распределения скоростей определяется

.

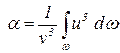(3.33)

Коэффициент неравномерности распределения скоростей определяется в зависимости от режимов движения жидкости

Ламинарный режим	Турбулентный режим	V ®¥
a = 2	a = 1,1¸1,2	a = 1

На практике обычно выбирают значение a = 1.

При применении уравнения Бернулли следует придерживаться следующих правил:

1. Выбрать два поперечных сечения. Поперечные сечения выбираются по направлению движения жидкости в начале потока 1 – 1 в конце 2 - 2. Поперечные сечения выбираются там, где известны давления или где одно из давлений необходимо найти.

2. Выбирают плоскость сравнения 0 - 0. Плоскостью сравнения может служить любая горизонтальная поверхность. Обычно выбирают плоскость сравнения, проходящую через центр тяжести нижнего поперечного сечения.

3. Записывают значения z и p для поперечных сечений. Для напорных потоков (движение жидкости в трубе) за характерную точку обычно принимают центр тяжести трубы. Для безнапорных потоков (движение жидкости в реке) за характерную точку обычно принимают точку на свободной поверхности жидкости. Давление p должно иметь один и тот же тип или абсолютное в обеих частях уравнения или манометрическое.

4. Расписывают скорости в поперечных сечениях. В уравнении Бернулли, как минимум, входят три скорости: v₁ – средняя скорость в первом сечении, v₂ – средняя скорость во втором сечении, v – средняя скорость в трубе, которая соединяет эти сечения (от этой скорости зависят потери напора h_1-2). Если известен расход, то скорости находятся:

.

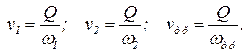(3.34)

Если расход неизвестен, то неизвестны и скорости. В этом случае удобно все скорости выразит через скорость в трубе:

.

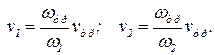(3.35)

Полученные значения z, p, v подставляют в уравнение Бернулли и находят неизвестную величину.

Дата добавления: 2014-01-07