Основное уравнение равномерного движения

Найдем общее выражение для потерь напора на трение при равномерном движении жидкости в трубах, которое справедливо и для ламинарного и для турбулентного режимов движения. При равномерном движении средняя скорость и распределение скоростей по сечению должны оставаться неизменными по длине трубопровода, поэтому равномерное движение возможно лишь в трубах постоянного сечения.

Составляя уравнение Бернулли для двух сечений трубопровода постоянного сечения (см. рисунок 4.4) и учитывая, что для горизонтальной трубы z₁ = z₂ и средние скорости в сечениях равны v₁ = v₂, а из потерь напора будут только потери напора на трение h_тр, имеем:

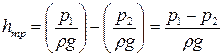
(4.8)

Уравнение (4.8) является основным уравнением равномерного движения жидкости в трубопроводах. При известных отметках положения трубопровода (z₁ и z₂ заданы) и давления в одном из сечений это уравнение позволяет найти давление в другом сечении. Для этого нужно только определить потерянную энергию h_тр.

Рисунок 4.4 - К– к выводу уравнения равномерного движения.

Основному уравнению равномерного движения жидкости в трубопроводах можно придать также другой вид. Для этого выделим в трубопроводе радиусом r₀ между сечениями 1–1 и 2 - 2 соосный цилиндр радиусом r и длиной l (рисунок 4.4). На этот цилиндр со стороны окружающей жидкости действуют силы: в сечении 1-1 сила давления равная P₁ = p₁ p r², в сечении 2-2 сила давления равная P₂ = p₂ p r² и на боковую поверхность сила трения равная T = 2 p r l t. Так как движение равномерное, то сумма действующих на цилиндр сил равна нулю: P₁ - P₂ - T = 0. Уравнение динамического равновесия рассматриваемого цилиндра можно записать в виде

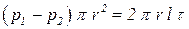
(4.9)

где t – сила сопротивления на единице площади поверхности жидкости цилиндра (касательное напряжение).

Разделив обе части этого уравнения на 2 л r l, получим:

.

(4.10)

Если выразить разность давлений через потери напора на трение получим:

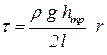
(4.11)

Касательное напряжение распределяется по линейному закону (см. рисунок 4.4) - оно равно нулю на оси трубы и принимает максимальное значение t₀ на стенке (r = r₀), где t₀= r g h_тр r₀ /(2 l). Отсюда следует:

(4.12)

Уравнение (4.11) представляет собой общее выражение для потерь напора при равномерном движении жидкости в трубопроводах круглого сечения. Это уравнение в одинаковой мере применимо как к ламинарному, так и к турбулентному режиму.

Дата добавления: 2014-01-07