Лекция 1. Элементы аналитической геометрии

Иные интеллектуальные субъективные права

В новом ГК РФ использован интересный юридико-технический прием - выделение иных интеллектуальных прав помимо исключительных и личных. Данный прием оставляет место в системе интеллектуальных прав для субъективных прав, которые не могут быть однозначно отнесены к имущественным исключительным правам, либо личным неимущественным правам.

К иным интеллектуальным правам следует отнести, в частности:

1) право следования (ст. 1293 ГК РФ);

2) право доступа (ст. 1292 ГК РФ);

3) право автора изобретение, полезной модели, промышленного образца, селекционного достижения на подачу заявки на получение патента (ст. 1357, 1420 ГК РФ);

4) право автора на вознаграждение за использование служебного РИД (п. 2 ст. 1295, ст. 1320, п. 4 ст. 1370, п. 5 ст. 1430, п. 4 ст. 1461 ГК РФ).

5) право композитора, создавшего музыкальное произведение для включения его в аудиовизуальное произведение, на вознаграждение за публичное исполнение такого музыкального произведения

6) право на наименование селекционного достижения (ст. 1419 ГК РФ).

Так же к иным интеллектуальным правам можно отнести права, очень похожие по признакам на личные неимущественные права, но прямо законом к таковым не отнесенные:

1) право лица, организовавшего создание сложного объекта, на указание своего имени (наименования) при его использовании (п. 4 ст. 1240 ГК РФ);

2) право издателя энциклопедий, энциклопедических словарей, периодических и продолжающихся сборников научных трудов, газет, журналов и других периодических изданий указывать свое наименование или требовать его указания при любом использовании издания (п. 7 ст. 1260 ГК РФ);

3) право изготовителя АВП при любом использовании АВП указывать свое имя или наименование либо требовать такого указания (п. 4 ст. 1263 ГК РФ);

4) право работодателя при использовании служебного произведения указывать свое имя или наименование либо требовать такого указания (п. 3 ст. 1295 ГК РФ);

5) право изготовителя фонограммы на указание на экземплярах фонограммы и (или) их упаковке своего имени или наименования (п. 1 ст. 1323 ГК РФ);

6) право изготовителя базы данных на указание на экземплярах базы данных и (или) их упаковках своего имени или наименования (п. 2 ст. 1333 ГК РФ);

7) право публикатора на указание своего имени на экземплярах обнародованного им произведения и в иных случаях его использования, в том числе при переводе или другой переработке произведения (п. 1 ст. 1338 ГК РФ).

Данные права подлежат защите способами, предусмотренными законом для защиты личных неимущественных интеллектуальных прав (п. 2 ст. 1251 ГК РФ).

1. Структура курса. Расчасовака, план занятий. План самостоятельной работы. Вопросы к экзамену – в конце курса.

2. В элементарной(школьной) геометрии изучаются свойства фигур и тел, причем основную роль играют построения для каждого конкретного случая, а вычислениям отводится вспомогательная роль. При этом для каждого случая применяется индивидуальный подход, что составляет основную трудность.

3. Аналитическая геометрия (АГ) была призвана устранить эти трудности и создать единый метод решения различных геометрических задач по изучению геометрических свойств объектов. Сущность этого метода заключается в том, что геометрическим объектам сопоставляются уравнения или системы уравнений, поэтому свойства объектов изучаются аналитически, а построениям, наоборот, отводится вспомогательная роль. Сам термин был предложен Ньютоном.

4. Основные понятия АГ на плоскости: точка, отрезок, линия (кривая), прямая линия (линия первого порядка), числовая ось, линии второго порядка: окружность, эллипс, гипербола, парабола, система координат.

5. Основные общие задачи АГ: 1) Дана линия, рассматриваемая как множество точек. Составить уравнение этой линии. 2) Дано уравнение некоторой линии. Изучить по нему ее геометрические свойства (форму и расположение).

6. Типовые задачи АГ, связанные с точкой.

1) Расстояние от начала координат до точки.

2) Расстояние между двумя точками.

3) Координаты середины отрезка.

4) Деление отрезка в заданном отношении.

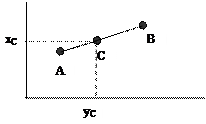
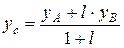
6. Прямая линия.

1) Уравнение через угловой коэффициент ;

2) Общее уравнение прямой . Связь между 1) и 2).

3) Уравнение прямой, проходящей через точку M(x ₁; y ₁): . Преобразование к виду 1) на примере.

4) Уравнение прямой, проходящей через две точки. Преобразование к виду 1) на примере.

7. Взаимное расположение прямых: пересекающиеся, совпадающие, параллельные, перпендикулярные. Прямые заданы уравнениями:

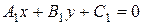; или ;

1) Условие пересечения: 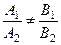. Точка пересечения М имеет координаты:

2) Условие совпадения: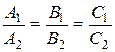

3) Условие параллельност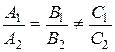и: или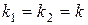

4) Условие перпендикулярност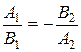и: или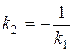

8. Самостоятельно проходите:

1) Угол между двумя пересекающимися прямыми.

2) Определение площади треугольника по координатам его вершин.

3) Решение систем двух линейных уравнений (сводится к решению задачи об определении координат точки пересечения двух прямых).

4) Расстояние точки до прямой линии.

5) Векторы. Сложение векторов. Скалярное и векторное произведение векторов.

9. Линии второго порядка. Окружность. Каноническое уравнение.

Это геометрическое место точек, равноудаленных от точки, являющейся центром окружности. Уравнение окружности с центром, совпадающим с началом координат: . Уравнение окружности с центром, не совпадающим с началом координат и имеющим координаты C(x_C;y_C): .

10. Линии второго порядка. Эллипс. Каноническое уравнение:

Это геометрическое место точек плоскости, сумма расстояний которых от двух данных точек, называемых фокусами есть величина постоянная.

Большая ось, большая полуось (a), малая ось, малая полуось (b), фокусы (-c; c), фокусное расстояние (2c), фокальные радиусы (r₁; r₂). Свойства эллипса: 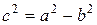; 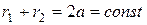. Эксцентриситет эллипса .

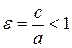11. Линии второго порядка. Гипербола. Каноническое уравнение:

Это геометрическое место точек плоскости, разность расстояний которых от двух данных точек, называемых фокусами есть величина постоянная.

Действительная ось (A₁;A₂), действительная полуось (a), мнимая ось (В₁;В₂), мнимая полуось (b), фокусы (-c; c), фокусное расстояние (2c), фокальные радиусы (r₁; r₂).

Свойства гиперболы: ; 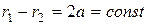. Эксцентриситет гиперболы . Асимптоты .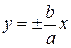

12. Линии второго порядка. Парабола. Напомнить о параболе в школе (квадратный трехчлен)

Каноническое уравнение:

Это геометрическое место точек на плоскости равноудаленных от фокуса и прямой, называемой директрисой.

Лекция 2. Введение в математический анализ (МА)

1. Темы, которые сейчас называют высшей математикой, начались разрабатываться с середины 17 в., когда математики начали исследовать переменные величины. Благодаря этому в математику вошло движение, что привело к появлению дифференциального и интегрального исчисления. Основой высшей математики является математический анализ, который основывается на понятии функции и на исчислении бесконечно малых величин. Важными понятиями МА являются функция, предел, непрерывность функции, производная и интеграл.

2. Понятие функции.

Величина называется функцией аргумента x, если каждому допустимому значению x можно привести каким-либо способом в соответствие одно или несколько значений y. Функцию можно задать аналитически, графически или таблично. Примеры однозначных функций: линейная, обратно пропорциональная; квадратичная, степенная, показательная, тригонометрическая.

3. Область определения функции (область существования функции, ОДЗ) – совокупность всех допустимых значений независимой переменной x (т.е. аргумента).

4. Область изменения функции (область значений функции) – диапазон значений функции y(x) в диапазоне изменения аргумента.

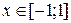Пример. . ОДЗ: ОЗФ:

5. Основные свойства функций:

1) монотонность (возрастание и убывание);

2) четность или нечетность;

3) периодичность;

4) непрерывность.

6. Понятие предела. Предел числовой последовательности. Числовая последовательность стремится к некоторому пределу а , если отличается от а сколь угодно мало, начиная с некоторого достаточно большого номера n: .

Предел функции. Число b называется пределом функции (т.е. ) при , если для любого (малого) числа ε>0 найдется такое (малое) число δ>0, когда выполняется условие: 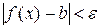при .

В этом случае пишут так: . Геометрический смысл предела поясняется рисунком.

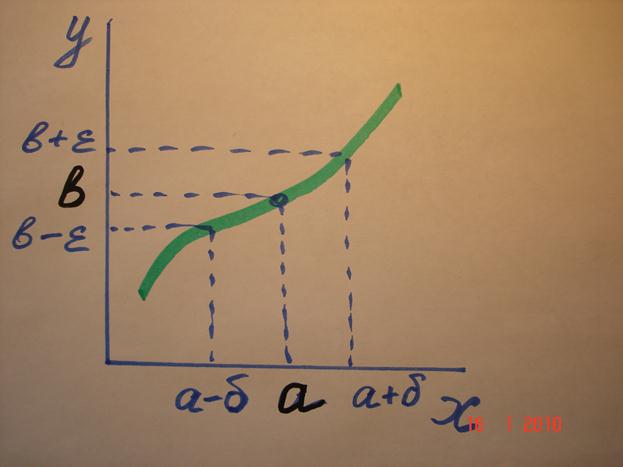
Внимание: речь идет об окрестностях точек, а не о самих точках.

Простейший способ вычисления пределов – подстановка аргумента в функцию.

7. Самостоятельно: основные теоремы о пределах: предел постоянной величины; предел суммы функций; предел разности функций; предел произведения функций; предел частного от деления функций.

Самостоятельно: первый и второй замечательные пределы.

8. Понятие о бесконечно больших и бесконечно малых.

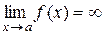Функция называется бесконечно большой при , если . Пример: 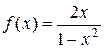при .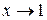

Функция 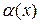называется бесконечно малой при , если .

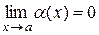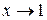Примеры. при . при .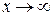

9. Приращение аргумента и приращение функции. Положительное и отрицательное приращение.

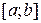10. Непрерывность функции. Функция , заданная на отрезке , является непрерывной в точке 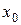этого отрезка, если ее приращение , соответствующее приращению 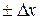, стремится к нулю при 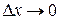, т.е.: . Если это не выполняется, то функция называется разрывной в этой точке, а сама точка называется точкой разрыва.

11. Производная функции. Общее определение производной как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

12. Скорость в механике как производная пути по времени: механический смысл производной.

13. Понятие касательной: предельное положение секущей. Геометрический смысл производной: она равна угловому коэффициенту касательной к графику функции в точке касания. Вывод самостоятельно. Связь между непрерывностью функции и ее дифференцируемостью. Роль производной в различных процессах.

14. Понятие о дифференциале. Геометрический смысл дифференциала: главная часть приращения функции.

15. Самостоятельно. Производные некоторых функций. Правила вычисления производных: производная суммы и разности функций; производная произведения функций; производная частного от деления функций. Производная сложной функции. Понятие о производных высших порядков. Экстремумы функций. Связь между знаком производной и возрастанием и убыванием функции. Геометрический

16. Правило Лопиталя. Неопределенност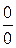и и при вычислении пределов и применение правила Лопиталя для вычисления таких пределов.

17. Неопределенный интеграл. Задача интегрального исчисления является обратной задаче дифференциального исчисления. Понятие первообразной, бесчисленное множество первообразных. Метод непосредственного интегрирования: 1)простых выражений; 2)использующий правило: интеграл суммы/разности функций равен сумме/разности интегралов; 3) использующий алгебраические преобразования. Метод интегрирования заменой переменной.

18. Определенный интеграл. Формула Ньютона-Лейбница. Применение определенного интеграла для нахождения площадей геометрических фигур.

Дата добавления: 2014-01-07